Excelで道路照明灯基礎の設計計算 -H24設計便覧（案）の直接基礎-
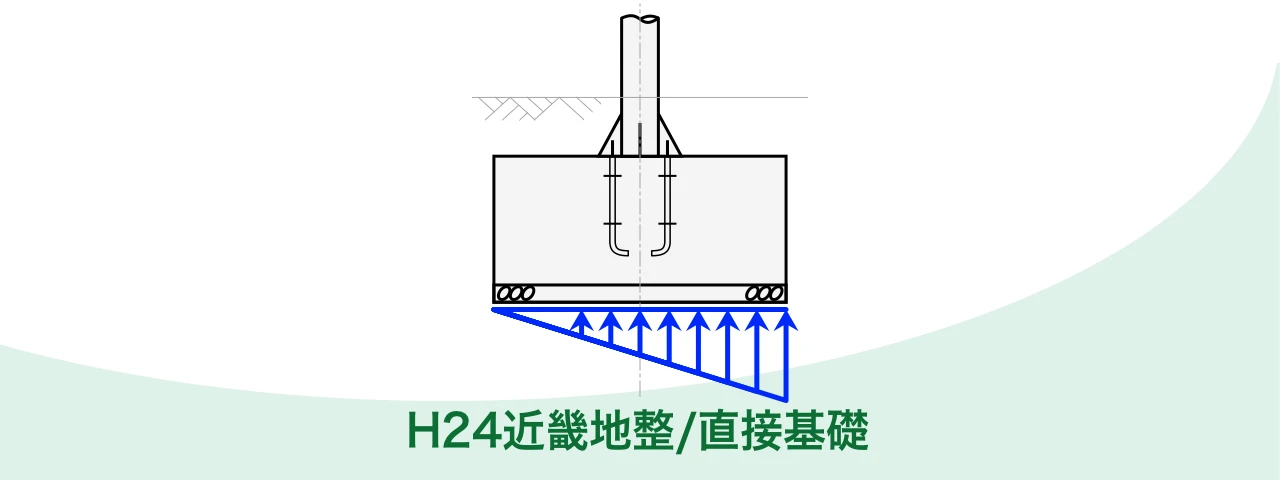
この記事では、道路照明灯の基礎をエクセルで設計計算してみた結果をご紹介します。
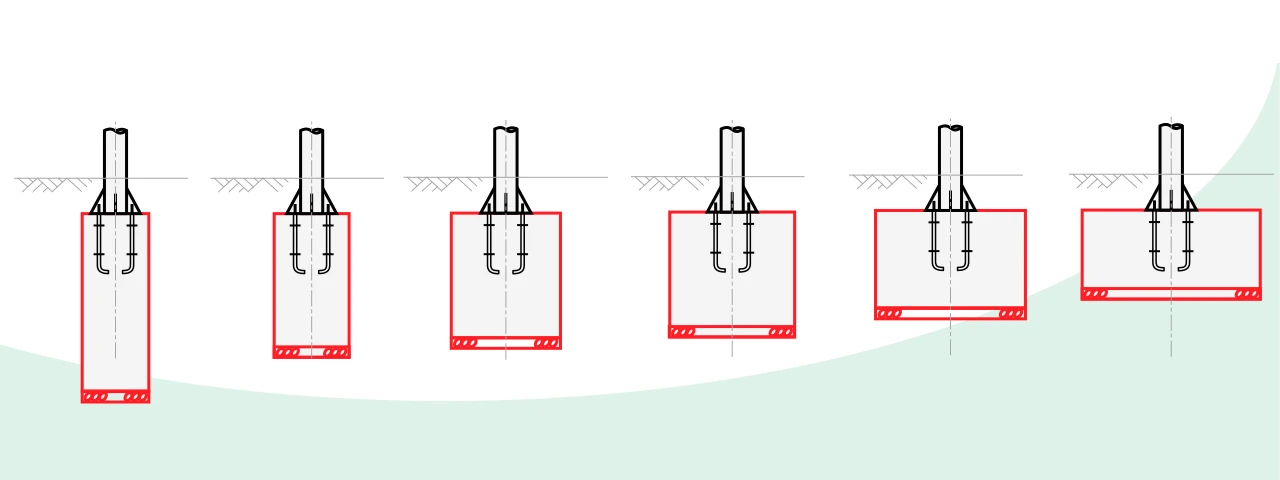
先にご紹介した「昭和50年建設省通知」と「JIL1003:2009と土木研究所資料第1035号｣に基づいたそれぞれの設計計算例では、基礎寸法を表から選択する設計でした。
Excelで道路照明灯基礎の設計計算 -S50建設省通知-
この記事では、道路照明灯の基礎をエクセルで設計計算してみた結果をご紹介します。基礎の設計方法はいくつかありますが、今回紹介する設計方法は、昭和50年の建設省（現：国土交通省）通知を元にしています。
Excelで道路照明灯基礎の設計計算 -JIL1003:2009、土研第1035号-
この記事では、道路照明灯の基礎をエクセルで設計計算してみた結果をご紹介します。ここで紹介する設計計算例では、平成24年に近畿地方整備局が発行した設計便覧（案）に基づいています。
これらの表から選択できる基礎形状よりも、さらに基礎の高さの小さくしたい場合、「直接基礎」の計算により安定を照査します。
1. 設計方法（準拠する基準書）
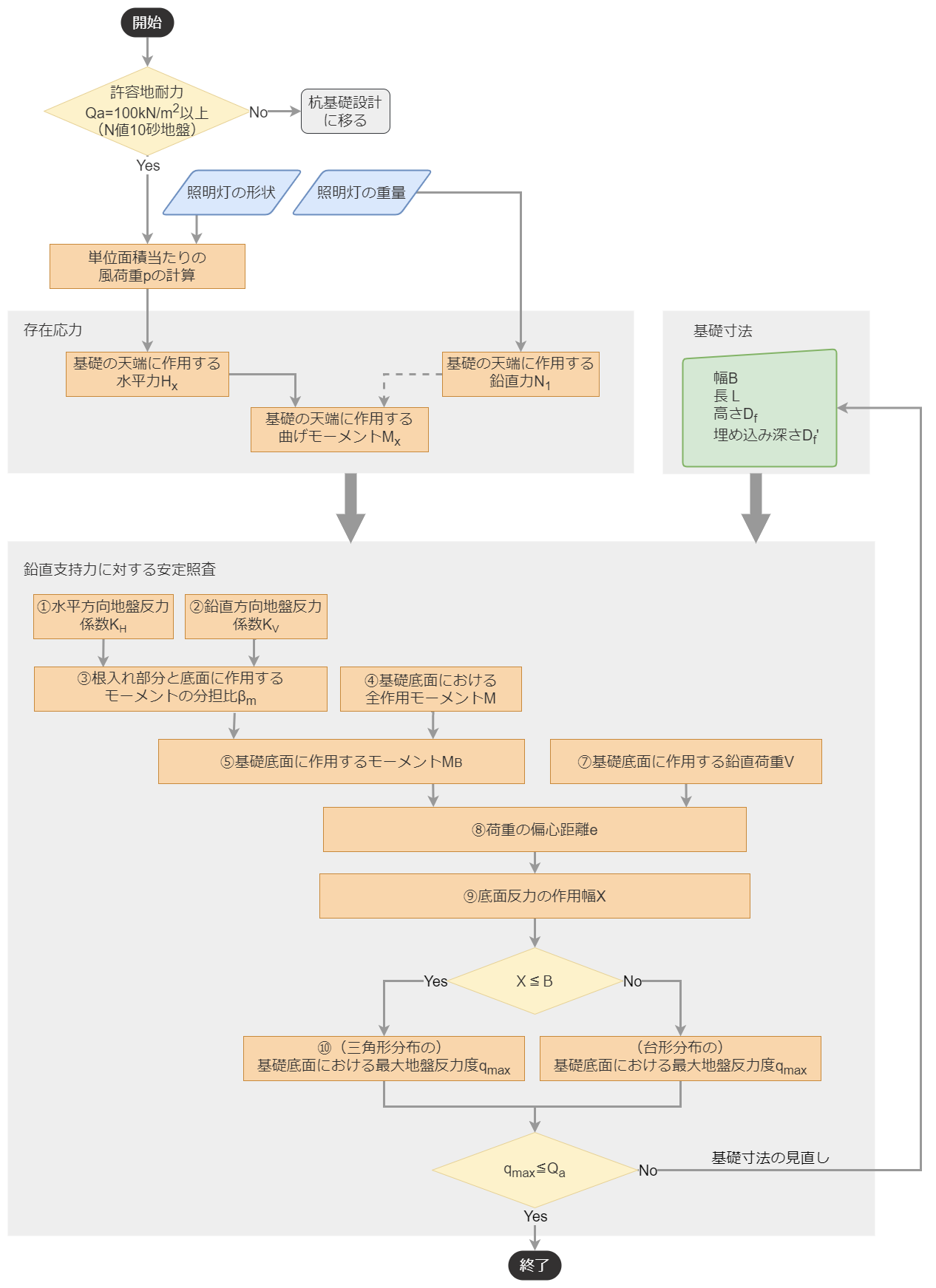
近畿地方整備局がWebサイトで公開している「設計便覧（案）ー第４編電気通信編ー第４章道路照明設備ー第４節 照明柱等基礎（p.4-54からp.4-57）」より、水平力$H_x$、曲げモーメント$M_x$、鉛直力$N_1$を計算したうえ、基礎の寸法を定め、「鉛直支持力に対する安定照査」を行う。
設計の流れは下記フローチャートのとおりです。（クリックすると別ウィンドウで開きます。）
| 📌NOTE |
|---|
|
2. 設計条件（設計風速と支柱形状）
許容地耐力$Q_a=100 \ \mathrm{kN/m^2}$とする。（N値10程度の砂質地盤相当）
器具は「車道用の道路照明灯」とし、設計風速は「$V_{cr}=60 \ \mathrm{m/sec}$」とする。
支柱は「直線型テーパーポール 可変型 ベース式埋設型」とし、その形状寸法は、JIL1001:2019「照明用テーパーポール（鋼製）」p.24の「IA12.3B-C」のとおりとする。
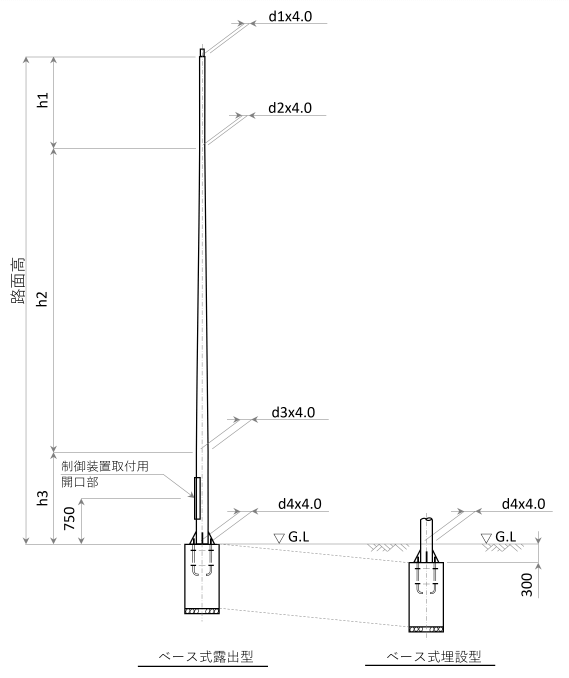
| 路面高 | $h_1$ | $h_2$ | $h_3$ | $d_1$ | $d_2$ | $d_3$ | $d_4$ |
|---|---|---|---|---|---|---|---|
| 12,000 | 2,500 | 8,000 | 1,500 | 75 | 75 | 195 | 195 |
出所:JIL1001:2019「照明用テーパーポール（鋼製）」(単位:mm)
| 📌NOTE |
|---|
|
3. 支柱下端から基礎天端への作用力
3-1. 単位面積当たりの風荷重pの計算
- $p$：有効投影面積当り風荷重（N/m²）
- $C$：風力係数（ポール丸形0.7、照明器具道路灯1.0）
- $V_{cr}$：設計風速（m/sec）
よって、単位面積あたりの風荷重は次のとおり。
| 📌NOTE |
|---|
|
3-2. 水平力Hxの計算
水平力の計算式は「水平力$H$＝受圧面積$A$ x 単位面積当たりの風荷重$p$」である。
よって、次表のとおり計算され、基礎の天端に作用する水平力$H_x$は「$2,705.50\ \mathrm{N}$」となる。
| 部位 | 受圧面積計算式 | 受圧面積 $A$ (m²) |
風荷重 $p$ （N/m²） |
水平力 $H_x$ (N) |
|---|---|---|---|---|
| 器具 | JIL1001:2019のp.5 | 0.13 | 2,214.00 | 287.82 |
| 支柱上段 | $h_1 \cdot d_2$ | 0.19 | 1,549.80 | 294.46 |
| 支柱中段 | $\displaystyle h_2 \cdot \frac{d_2 + d_3}{2}$ | 1.08 | 1,549.80 | 1,673.78 |
| 支柱下段 | $h_3 \cdot d_4$ | 0.29 | 1,549.80 | 449.44 |
| 合計 | 2,705.50 |
| 📌NOTE |
|---|
|
3-3. 曲げモーメントMxの計算
曲げモーメントの計算式は「曲げモーメント$M$＝アーム長$L$ x 水平力$H$」である。
よって、次表のとおり計算され、基礎の天端に作用する曲げモーメント$M_x$は「$15,986.27\ \mathrm{N \cdot m}$」となる。
| 部位 | アーム長の計算式 | アーム長 $L$ (m) |
水平力 $H_x$ (N) |
曲げモーメント $M_x$ (N・m) |
|---|---|---|---|---|
| 器具 | $h_1 + h_2 + h_3 + 300$ | 12.30 | 287.82 | 3,540.19 |
| 支柱上段 | $\displaystyle \frac{ h_1}{2} + h_2 + h_3 + 300$ | 11.05 | 294.46 | 3,253.78 |
| 支柱中段 | $\displaystyle h_2 \cdot \frac{d_3 + 2 \cdot d_2}{ 3 \cdot (d_3 + d_2)} + h_3 +300$ | 5.21 | 1,673.78 | 8,720.39 |
| 支柱下段 | $\displaystyle \frac{ h_3 }{2}+300$ | 1.05 | 449.44 | 471.91 |
| 合計 | 2,705.50 | 15,986.27 |
| 📌NOTE |
|---|
|
3-4. 鉛直力N₁の計算
基礎の天端に作用する鉛直力$N_1$は、器具と支柱の重量とし、次表のとおり計算され「$2,450 \ \mathrm{N}$」となる。
| 仕様 | 長さ (m) |
重量 (N) |
備考 |
|---|---|---|---|
| 器具 | 0.7 | 98.00 | 10kg |
| 梁材 | 0 | 0 | |
| 支柱 | 12 | 2,352.00 | 240kg |
| 合計 | 2,450.00 |
| 📌NOTE |
|---|
|
4. 基礎の設計計算
4-1. 基礎寸法
次のとおりに仮定します。
- 幅 $B = 1,300\ \mathrm{mm}\ =\ 1.3\ \mathrm{m}$
- 長 $L = 1,300\ \mathrm{mm}\ =\ 1.3\ \mathrm{m}$
- 高さ$D_f = 650\ \mathrm{mm}\ =\ 0.65\ \mathrm{m}$
- 埋め込み深さ ${D_f}^\prime = 300\ \mathrm{mm}\ =\ 0.3\ \mathrm{m}$
| 📌NOTE |
|---|
|
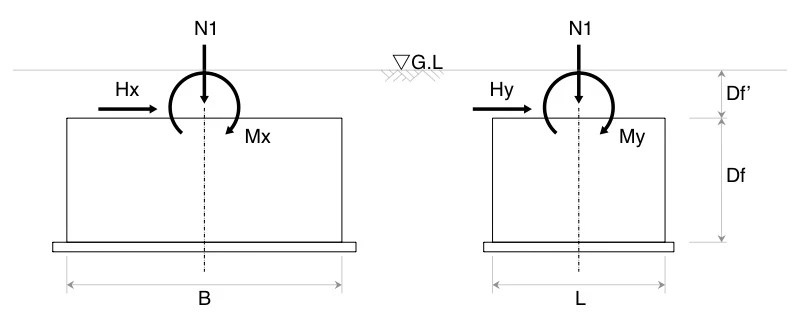
4-2. 存在応力
支柱下端から基礎天端への作用力をまとめると、下表のとおり。
| 直風時(N) | (kN) | |
|---|---|---|
| 鉛直力$N_1$ | 2,450 | 2.45 |
| 水平力$H_x$ | 2,705 | 2.71 |
| 曲げモーメント$M_x$ | 15,986 | 15.99 |
4-3. 鉛直支持力に対する安定照査
鉛直支持力に対する安定照査は、２つの方法があります。
- 荷重を「底面」のみで支持させる方法
- 荷重を「底面」と「根入れ部分」と分担して支持させる方法
今回の計算例では、基礎を300mm埋め込むため、荷重を「底面」と「根入れ部分」と分担して支持させる方法となります。
| 📌NOTE |
|---|
照査の手順は下記のとおり。
|
4-3-1. 水平方向地盤反力係数 KH
$$
\begin{equation}
\begin{split}
K_H &= K_{H0} \cdot \left( \frac{B_H}{0.3} \right)^{-\frac{3}{4}} \\[0.5em]
&= \frac{1}{0.3} \times \alpha \times E_0 \times {A_H}^{-\frac{3}{8}} \times \left( \frac{1}{0.3} \right)^{-\frac{3}{4}}\\[0.5em]
&= 3.33 \times 1 \times 2,800 \cdot N \times \left( L \times D_f \right) ^{-\frac{3}{8}} \times 0.405 \\[0.5em]
&= 1.35 \times 2,800 \times 10 \times \left( L \times D_f \right) ^{-\frac{3}{8}} \\[0.5em]
&= 37,834 \times \left( L \times D_f \right) ^{-\frac{3}{8}} \\[0.5em]
&= 37,834 \times \left( 1.3 \times 0.65 \right) ^{-\frac{3}{8}} \\[0.5em]
&= 40,300 \ \mathrm{kN/m^3}
\end{split} \label{KH}
\end{equation}
$$
ここで
- $K_{H0}$：直径0.3mの剛体円板による平板載荷試験の値に相当する水平方向の地盤反力係数(kN/m³)
- $\displaystyle K_{H0} = \frac{1}{0.3} \times \alpha \times E_0$
- $\alpha$：地盤反力係数の推定に用いる係数（常時・暴風時：１、地震時：２）
- $\alpha =1$
- $E_0$：設計の対象とする位置での地盤の変形係数(kN/m²)
- $E_0 = 2,800 \times N$
- $N=10$:標準貫入試験のN値
- $\alpha$：地盤反力係数の推定に用いる係数（常時・暴風時：１、地震時：２）
- $\displaystyle K_{H0} = \frac{1}{0.3} \times \alpha \times E_0$
- $B_H$：荷重作用方向に直交する基礎の換算載荷幅(m)
- $B_H = \sqrt{A_H}$
- $A_H$：水平方向の載荷面積(m²)
- $A_H = L \times D_f$
- $A_H$：水平方向の載荷面積(m²)
- $B_H = \sqrt{A_H}$
| 📌NOTE |
|---|
|
4-3-2. 鉛直方向地盤反力係数 KV
$$
\begin{equation}
\begin{split}
K_V &= K_{V0} \cdot \left( \frac{B_V}{0.3} \right)^{-\frac{3}{4}} \\[0.5em]
&= \frac{1}{0.3} \times \alpha \times E_0 \times {A_V}^{-\frac{3}{8}} \times \left( \frac{1}{0.3} \right)^{-\frac{3}{4}}\\[0.5em]
&= 3.33 \times 1 \times 2,800 \cdot N \times \left( B \times L \right) ^{-\frac{3}{8}} \times 0.405 \\[0.5em]
&= 1.35 \times 2,800 \times 10 \times \left( B \times L \right) ^{-\frac{3}{8}} \\[0.5em]
&= 37,834 \times \left( B \times L \right) ^{-\frac{3}{8}} \\[0.5em]
&= 37,834 \times \left( 1.3 \times 1.3 \right) ^{-\frac{3}{8}} \\[0.5em]
&= 31,076 \ \mathrm{kN/m^3}
\end{split}\label{KV}
\end{equation}
$$
ここで
- $K_{V0}$：直径$0.3m$の剛体円板による平板載荷試験の値に相当する鉛直方向の地盤反力係数(kN/m³)
- $\displaystyle K_{V0} = \frac{1}{0.3} \times \alpha \times E_0$
- $\alpha$：地盤反力係数の推定に用いる係数（常時・暴風時：１、地震時：２）
- $\alpha =1$
- $E_0$：設計の対象とする位置での地盤の変形係数(kN/m²)
- $E_0 = 2,800 \times N$
- $N=10$:標準貫入試験のN値
- $\alpha$：地盤反力係数の推定に用いる係数（常時・暴風時：１、地震時：２）
- $\displaystyle K_{V0} = \frac{1}{0.3} \times \alpha \times E_0$
- $B_V$：基礎の換算載荷幅(m)
- $B_V = \sqrt{A_V}$
- $A_V$：鉛直方向の載荷面積(m²)
- $A_V = B \times L$
- $A_V$：鉛直方向の載荷面積(m²)
- $B_V = \sqrt{A_V}$
| 📌NOTE |
|---|
|
4-3-3. 根入れ部分と底面に作用するモーメントの分担比 βm
式 \eqref{KH} 、式\eqref{KV}より
$$
\begin{equation}
\begin{split}
\beta_m &= \frac{K_H}{K_V} \cdot \left( \frac{D_f}{B} \right)^3 \\[0.5em]
&= \frac{40,300}{31,076} \times \left( \frac{0.65}{1.3} \right)^3 \\[0.5em]
&= 0.162
\end{split}\label{betam}
\end{equation}
$$
4-3-4. 基礎底面における全作用モーメント M
$$
\begin{equation}
\begin{split}
M &= M_x + H_x \cdot D_f\\[0.5em]
&= 15.99+2.71\times0.65 \\[0.5em]
&= 17.75 \ \mathrm{kN \cdot m}
\end{split}\label{M}
\end{equation}
$$
4-3-5. 基礎底面に作用するモーメント MB
式\eqref{betam}、式\eqref{M}より
$$
\begin{equation}
\begin{split}
M_B &= \frac{1}{1+ \beta_m}\cdot M\\[0.5em]
&= \frac{1}{1+0.162}\times17.75 \\[0.5em]
&= 15.28 \ \mathrm{kN \cdot m}
\end{split}\label{MB}
\end{equation}
$$
4-3-6. 基礎底面を中心とする根入れ部分に作用するモーメント MS
式\eqref{betam}、式\eqref{M}より
$$
\begin{equation}
\begin{split}
M_S &= \frac{\beta_m}{1+ \beta_m}\cdot M\\[0.5em]
&= \frac{0.162}{1+0.162}\times17.75 \\[0.5em]
&= 2.48 \ \mathrm{kN \cdot m}
\end{split}\label{MS}
\end{equation}
$$
| 📌NOTE |
|---|
|
4-3-7. 基礎底面に作用する鉛直荷重 V
$$
\begin{equation}
\begin{split}
V &= N_1 + (\gamma_c \cdot B \cdot L \cdot D_f) + ( \gamma_s \cdot B \cdot L \cdot {D_f}^{\prime})\\[0.5em]
&= 2.45 + ( 23 \times 1.3 \times 1.3 \times 0.65 ) + ( 17 \times 1.3 \times 1.3 \times 0.3)\\[0.5em]
&= 36.33 \ \mathrm{kN}
\end{split}\label{V}
\end{equation}
$$
ここで
- $\gamma_c$：コンクリートの単位体積重量 $= 23 \ \mathrm{kN/m^3}$
- $\gamma_s$：土の単位体積重量 $= 17 \ \mathrm{kN/m^3}$
4-3-8. 荷重の偏心距離 e
式\eqref{MB}、式\eqref{V}より
$$
\begin{equation}
\begin{split}
e &= \frac{M_B}{V}\\[0.5em]
&= \frac{15.28}{36.33}\\[0.5em]
&= 0.42 \ \mathrm{m}
\end{split}
\end{equation}
$$
4-3-9. 底面反力の作用幅 X
$$
\begin{equation}
\begin{split}
X &= 3 \cdot \left( \frac{B}{2}-e \right)\\[0.5em]
&= 3 \cdot \left( \frac{1.3}{2}-0.42 \right)\\[0.5em]
&= 0.69 \ \mathrm{m}
\end{split}\label{X}
\end{equation}
$$
$(X= 0.69) \leqq (B=1.3)$ であるため、三角分布
| 📌NOTE |
|---|
|
4-3-10. 基礎底面における最大地盤反力度 qmax
式\eqref{V}、\eqref{X}より
$$
\begin{equation}
\begin{split}
q_{max} &= \frac{2\cdot V}{L \cdot X}\\[0.5em]
&= \frac{2\times 36.33}{1.3 \times 0.69}\\[0.5em]
&= 81.203 \ \mathrm{kN/m^2}
\end{split}\label{qmax}
\end{equation}
$$
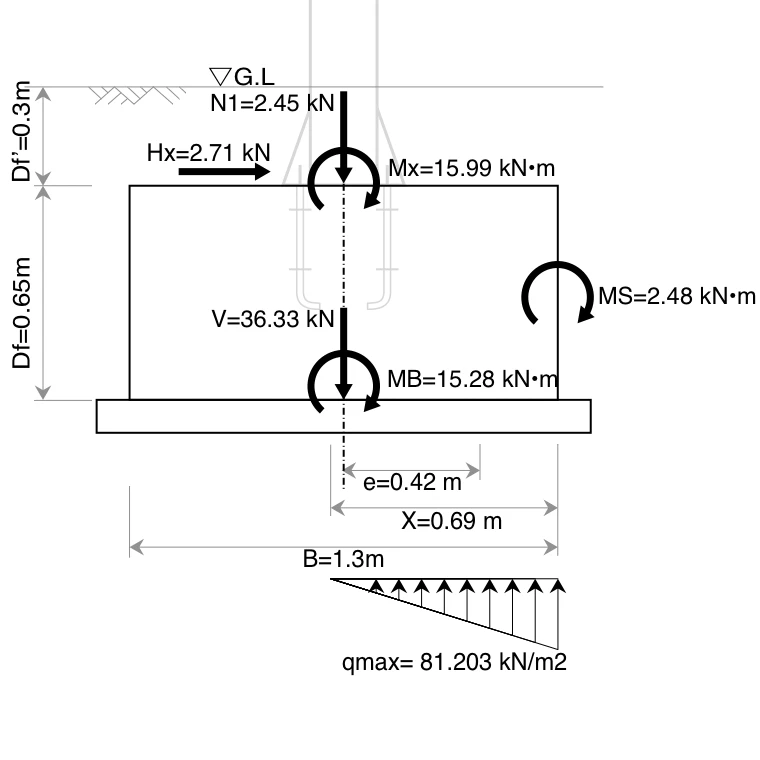
4-3-11. 判定
式\eqref{qmax}より
$q_{max} = 81.203 \leqq$ 許容地耐力$Q_a = 100\ \mathrm{kN/m^2}$
よって、OK
| 📌NOTE |
|---|
|
エクセルブック
計算を記載したエクセルブックは下記からダウンロードしてください。
もし、間違いなどを見つけられた場合は、ご連絡いただけると幸いです。
| 📌NOTE |
|---|
 Excelで道路照明灯基礎の設計計算 -R2道路標識構造便覧の直接基礎-
|
