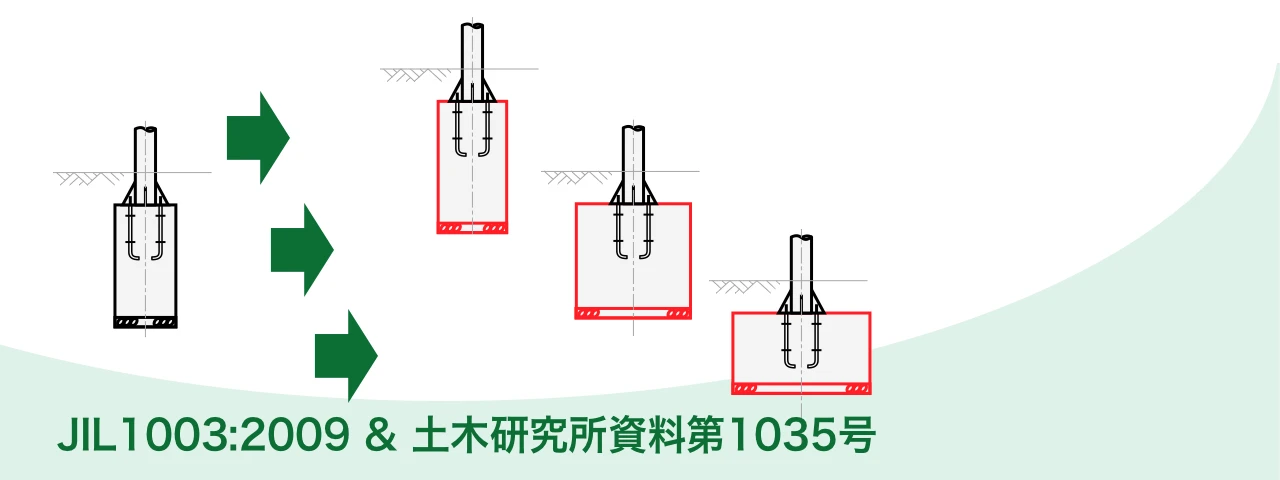
この記事では、道路照明灯の基礎をエクセルで設計計算してみた結果をご紹介します。

先にご紹介した「平成24年 近畿地方整備局 設計便覧（案）｣に基づいた道路照明灯の「直接基礎」の設計計算例では、基礎寸法を定め、「鉛直支持力」の安定照査を行う設計でした。

Excelで道路照明灯基礎の設計計算 -H24設計便覧（案）の直接基礎-

Excelで道路照明灯基礎の設計計算 -H24設計便覧（案）の直接基礎-

この記事では、道路照明灯の基礎をエクセルで設計計算してみた結果をご紹介します。平成24年に近畿地方整備局が発行した設計便覧（案）に基づいています。

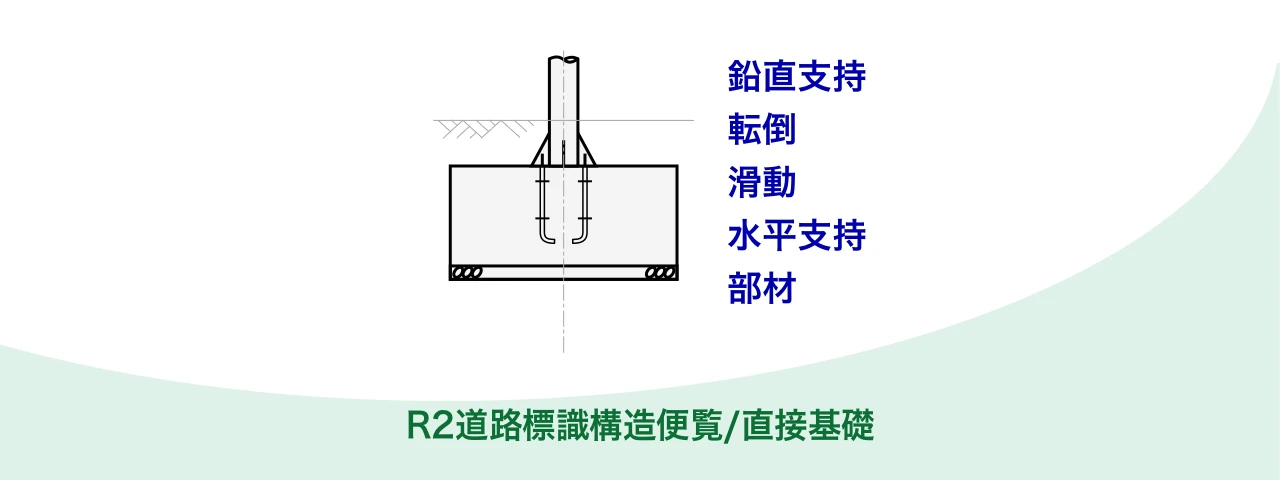
https://ce-note.com/light-foundation-h24kinki-chokusetsu/

この計算には、「転倒」、「滑動」、「水平支持力」の安定照査と、「部材」の照査が含まれていませんでした。

これから紹介する直接基礎の設計計算例では、これらを網羅している令和２年の道路標識構造便覧に基づいています。

1. 設計方法

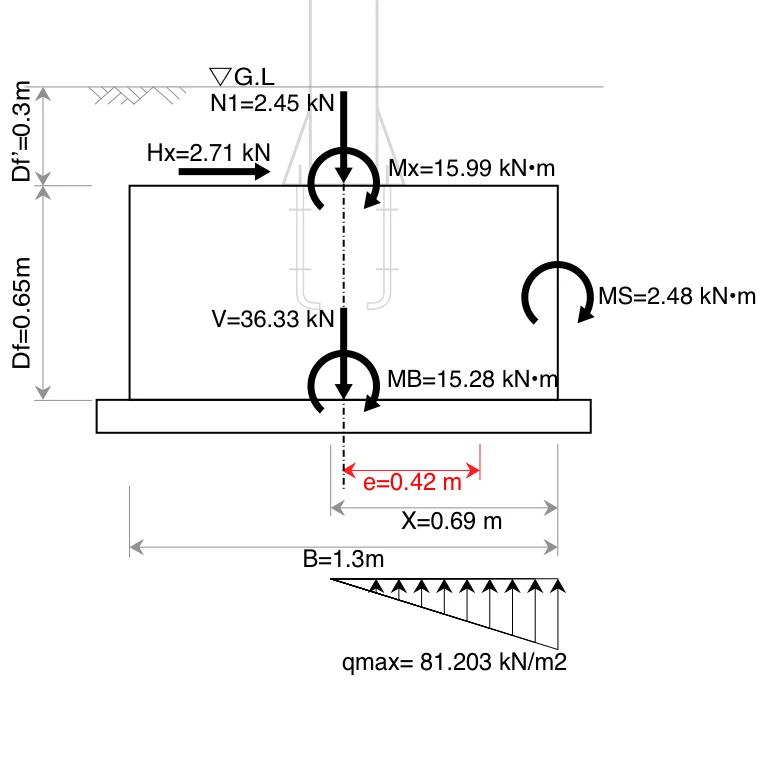
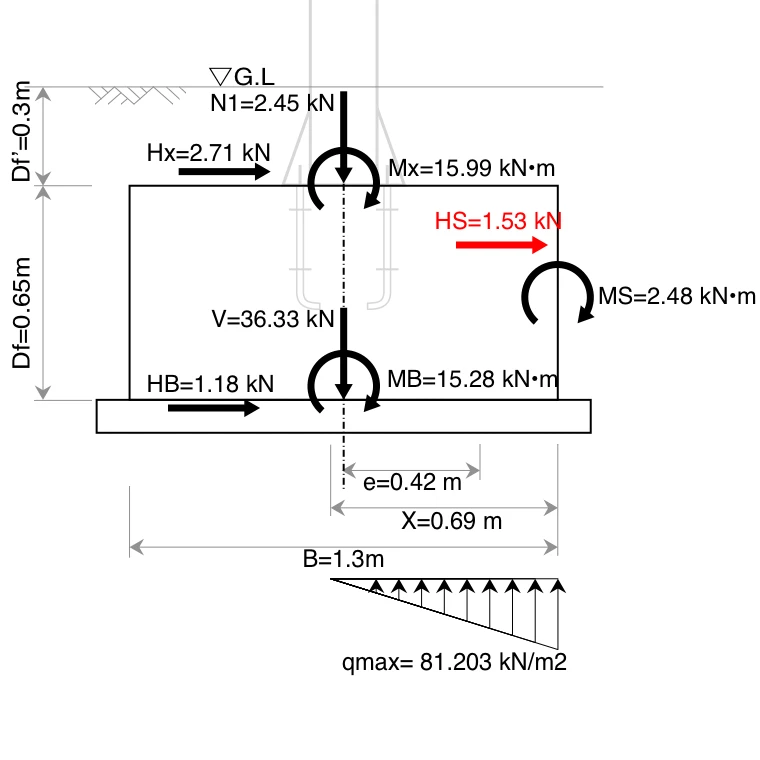
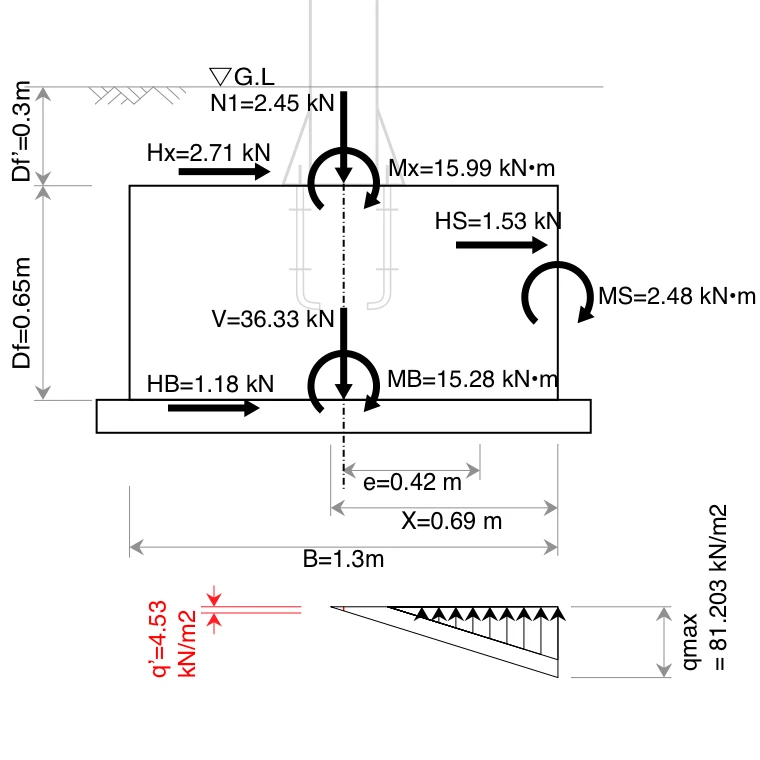
近畿地方整備局がWebサイトで公開している「設計便覧（案）ー第４編電気通信編ー第４章道路照明設備ー第４節　照明柱等基礎（p.4-54からp.4-57）」より、曲げモーメント$M_x$と水平力$H_x$、鉛直力$N_1$を計算したうえ、基礎の寸法を定め、「鉛直支持力に対する安定照査」を行う。

その結果から、さらに令和２年道路標識構造便覧（p.121からp.126、p.355から363）を参考に「転倒に対する安定照査」、「滑動に対する安定照査」、「水平支持力に対する安定照査」、「部材の照査」を行う。

📌NOTE
「4-3. 鉛直支持力に対する安定照査」までは、前回の記事と同じなので、「4-4. 転倒に対する安定照査」から書いていきます。

4. 基礎の設計計算

4-4. 転倒に対する安定照査

直接基礎に作用する荷重の合力の作用位置が、常時には底面の中心より底面幅の1/6以内、暴風時及び地震時には底面幅の1/3以内であれば、転倒に対して安定となります。（R2道路標識構造便覧p.121）

$$ \begin{equation} \begin{split} e = 0.42 &\leqq \frac{B}{3} \\[0.5em] &\leqq \frac{1.3}{3}\\[0.5em] &\leqq 0.43 \end{split}\nonumber \end{equation} $$ よって、OK
📌NOTE
  • 照明灯の設計には、風荷重$V_{cr}=60\mathrm{m/sec}$を作用力として考慮することから、それを「暴風時」として、底面幅の1/3で照査しています。

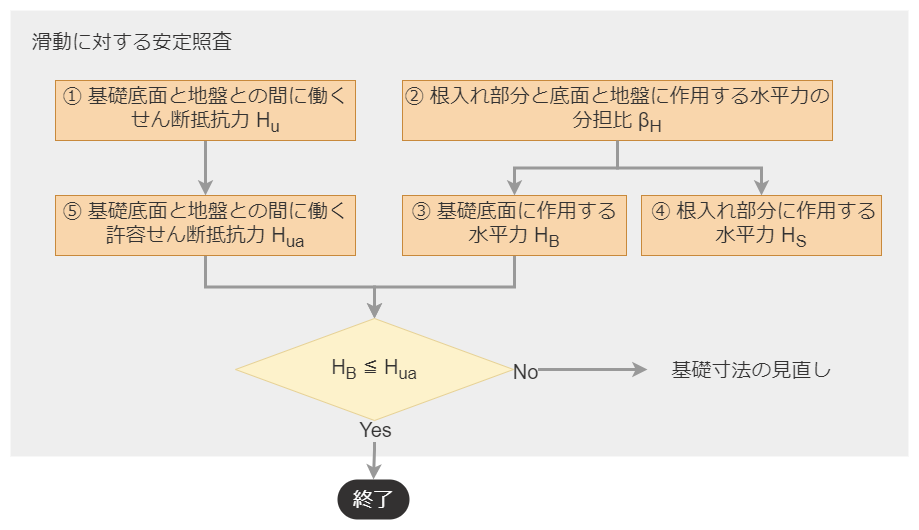
4-5. 滑動に対する安定照査

滑動に対する安定照査においても、鉛直支持力に対する安定照査と同様に、「底面」と「根入れ部分」とで水平力を分担させて照査します。

📌NOTE
照査の手順は下記のとおり。
  1. 「基礎底面に作用する鉛直荷重 $V$」と「基礎底面に作用する摩擦係数 $\mu$」から、「基礎底面と地盤との間に働くせん断抵抗力 $H_u$」を求める。
  2. 「水平方向せん断地盤反力係数 $k_S$」を求め、「根入れ部分と底面に作用する水平力の分担比 $\beta_H$」を求める。
  3. $\beta_H$と「基礎の天端に作用する水平力 $H_x$」から「基礎底面に作用する水平力 $H_B$」を求める。
  4. $\beta_H$と「基礎の天端に作用する水平力 $H_x$」から「根入れに作用する水平力 $H_S$」を求める。
  5. $H_u$から、「基礎底面と地盤との間に働く許容せん断抵抗力 $H_{ua}$」を求める。
  6. $H_B \leqq H_{ua}$を満足すれば、照査終了。

4-5-1. 基礎底面と地盤との間に働くせん断抵抗力 Hu

$$ \begin{equation} \begin{split} H_u &= V \cdot \mu \\[0.5em] &= 36.33 \times 0.4\\[0.5em] &= 14.53 \ \mathrm{kN} \end{split}\label{Hu} \end{equation} $$

ここで

  • $\mu$：基礎底面に作用する摩擦係数
    • $\mu = 0.4$
📌NOTE
  • $\mu$は、道路案内標識基礎標準図集（関東地方建設局、1989）による推定式で、決まっています。（R2道路標識構造便覧p.122）
  • この$\mu =0.4$は、やや小さめ（つまり安全側）に設定されており、H24道路土工擁壁工指針p.70では0.5～0.7となっています。
  • さらに、R2道路標識構造便覧p.123には、H24道路橋示方書による$H_u$の推定式も記載されています。
  • 照明灯管理者の判断でどの基準書から値を採用するか決めるべきでしょう。
  • ちなみに、「基礎底面に作用する鉛直荷重　$V$」の値「36.33」は、前回の記事で「鉛直支持力に対する安定照査」の4-3-7で算出しています。

4-5-2. 根入れ部分と底面に作用する水平力の分担比 βH

$$ \begin{equation} \begin{split} \beta_H &= \frac{k_H \cdot D_f}{2 k_S\cdot B} \\[0.5em] &= \frac{40,300 \times 0.65}{2 \times \lambda \times k_V \times 1.3} \\[0.5em] &= \frac{26,195.1}{2 \times \frac{1}{4} \times 31,076 \times 1.3} \\[0.5em] &= 1.297 \end{split}\label{bH} \end{equation} $$

ここで

  • $k_S$：水平方向せん断地盤反力係数（kN/m³）
    • $k_S= \lambda \cdot k_V$
      • $\lambda$：鉛直方向の地盤反力係数に対する水平せん断地盤反力係数の比
        • $\displaystyle \lambda = \frac{1}{4}$
📌NOTE
  • $\lambda$は、R2道路標識構造便覧の計算例で「1/4」と記載されていますが、出典や値の決定根拠は特に書いてありません。
  • H29道路橋示方書Ⅳのp.223では「0.3」となっており、「1/2～1/5の間の平均的な値」とされています。
  • なお、$k_H=40,300$、$k_V=31,076$、$D_f=0.65$、$B=1.3$の算出根拠は、前回記事をご覧ください

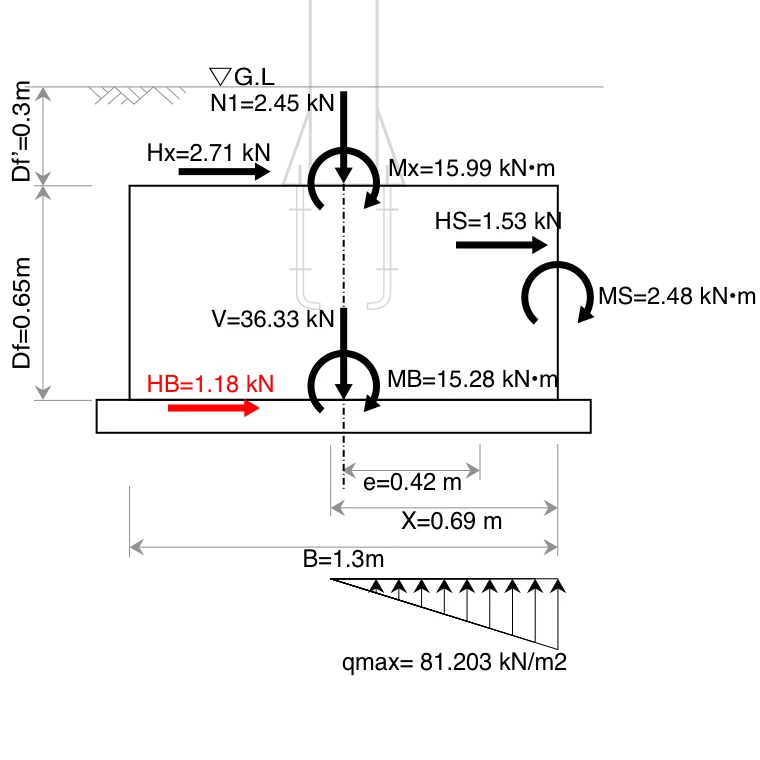
4-5-3. 基礎底面に作用する水平力 HB

式\eqref{bH}より

$$ \begin{equation} \begin{split} H_B &= \frac{1}{1+ \beta_H}H_x\\[0.5em] &= \frac{1}{1+1.297}\times2.71\\[0.5em] &= 1.18\ \mathrm{kN} \end{split}\label{HB} \end{equation} $$
📌NOTE
  • $H_x=2.71$の算出根拠は、前回記事をご覧ください


4-5-4. 根入れ部分に作用する水平力 HS

式\eqref{bH}より

$$ \begin{equation} \begin{split} H_S &= \frac{ \beta_H }{1+ \beta_H}H_x\\[0.5em] &= \frac{1.297}{1+1.297} \times 2.71\\[0.5em] &= 1.53\ \mathrm{kN} \end{split}\label{HS} \end{equation} $$
📌NOTE
$H_S$は、「滑動に対する安定照査」では計算上不要ですが、後述する「水平支持力に対する安定照査」で必要となります。

4-5-5. 基礎底面と地盤との間に働く許容せん断抵抗力 Hua

式\eqref{Hu}より

$$\begin{equation} \begin{split} H_{ua} &= \frac{1}{n_h}H_u\\[0.5em] &= \frac{1}{1.2}\times14.534\\[0.5em] &= 12.11\ \mathrm{kN} \end{split}\label{Hua} \end{equation} $$

ここで

  • $n_h$：基礎底面地盤の許容せん断抵抗力の安全率（常時1.5、暴風時及び地震時1.2）
    • $n_h = 1.2$
📌NOTE
照明灯の設計では風荷重が対象なので、「暴風時」として$n_h = 1.2$としています。

4-5-6. 判定

式\eqref{HB}、式\eqref{Hua}より

\begin{equation} \begin{split} H_B &= 1.18\ \mathrm{kN} \ \leqq \ H_{ua}=12.11 \ \mathrm{kN} \end{split}\nonumber \end{equation} よって、OK

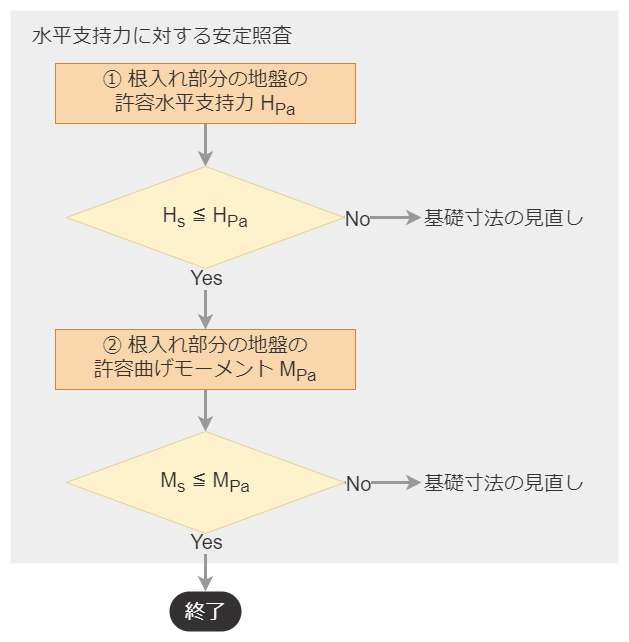
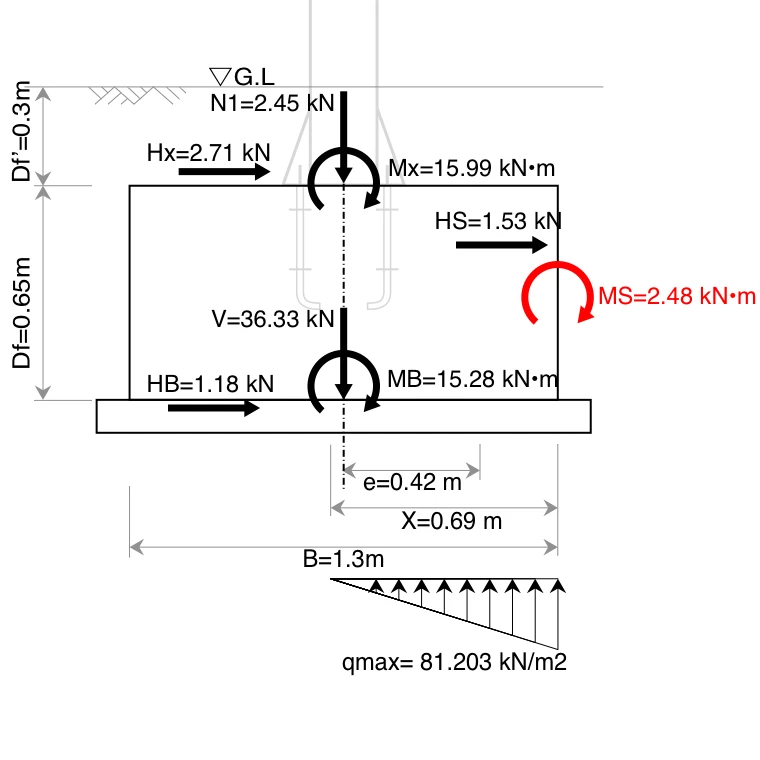
4-6. 水平支持力に対する安定照査

「鉛直支持力に対する安定照査」および「滑動に対する安定照査」で設定したとおり、「底面」と「根入れ部分」で作用力を分担するため、「水平支持力に対する安定照査」を行う必要があります。

📌NOTE
照査の手順は下記のとおり。
  1. 「根入れ部分の地盤の許容水平支持力 $H_{Pa}$」を求め、$H_S \leqq H_{Pa}$を満足すれば、照査の第一段階終了。
  2. 「根入れ部分の地盤の許容曲げモーメント $M_{Pa}$」を求め、$M_S\leqq M_{Pa}$を満足すれば、照査終了。

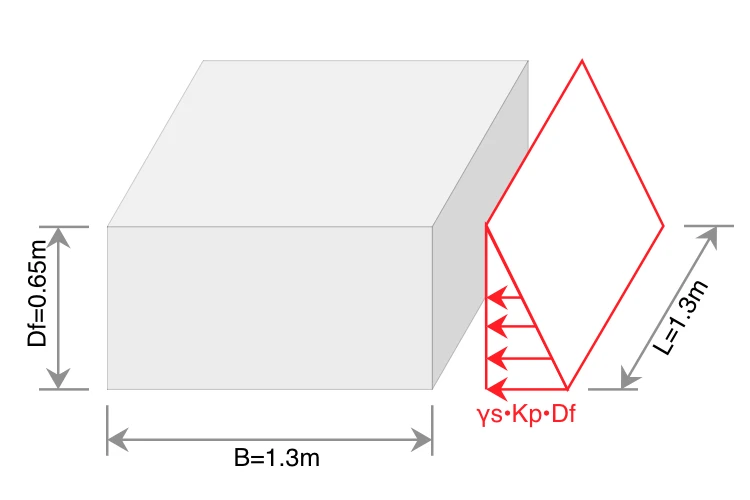
4-6-1. 根入れ部分の地盤の許容水平支持力 HPa

$$ \begin{equation} \begin{split} H_{Pa} &= \frac{1}{n_p}H_P\\[0.5em] &= \frac{1}{1.1}\times16.48\\[0.5em] &= 14.98\ \mathrm{kN} \end{split}\label{HPa} \end{equation} $$

ここで

  • $H_P$：根入れ部分の地盤の水平支持力（kN）
\begin{equation} \begin{split} H_P &= \frac{1}{2} \cdot \gamma_s \cdot K_P \cdot L \cdot {D_f}^2\\[0.5em] &= \frac{1}{2} \times 17 \times 3.53 \times 1.3 \times 0.65^2\\[0.5em] &= 16.48\ \mathrm{kN} \end{split}\nonumber \end{equation}
  • $K_P$：クーロン土圧による受働土圧係数
    • $K_P = 3.53$
  • $n_p$：地盤の許容水平支持力の安全率（常時1.5、暴風時及び地震時1.1）
    • $n_p =1.1$
📌NOTE
$K_P = 3.53$は、R2道路標識構造便覧p.357で突如登場する値ですが、次式のとおりせん断抵抗角で決まっています。 \begin{equation} \begin{split} K_P &= \tan^2(45 ^\circ + \frac{\phi}{2})\\[0.5em] &= \tan^2(45 ^\circ + \frac{34^\circ}{2})\\[0.5em] &= 3.53 \end{split}\nonumber \end{equation} ここで
  • $\phi$：せん断抵抗角
    • $\phi = 34^\circ$
設計条件が「N値10程度の砂質地盤」なので、妥当なせん断抵抗角の値でしょう。

式\eqref{HS}、式\eqref{HPa}より

\begin{equation} \begin{split} H_S &= 1.53\ \mathrm{kN} \ \leqq \ H_{Pa}=14.98 \ \mathrm{kN} \end{split}\nonumber \end{equation} よって、OK

4-6-2.根入れ部分の地盤の許容曲げモーメント MPa

$$ \begin{equation} \begin{split} M_{Pa} &= \frac{1}{n_p} \cdot M_P\\[0.5em] &= \frac{1}{1.1} \times 3.57\\[0.5em] &= 3.25\ \mathrm{kN \cdot m} \end{split}\label{MPa} \end{equation} $$

ここで

  • $M_P$：根入れ部分の地盤の曲げモーメント抵抗力（kN・m）
$$ \begin{equation} \begin{split} M_P &= \frac{1}{6} \cdot \gamma_s \cdot K_P \cdot L \cdot {D_f}^3\\[0.5em] &= \frac{1}{6} \times 17 \times 3.53 \times 1.3 \times 0.65^3\\[0.5em] &= 3.57 \ \mathrm{kN \cdot m} \end{split}\nonumber \end{equation} $$

式\eqref{MPa}より

\begin{equation} \begin{split} M_S &= 2.48\ \mathrm{kN \cdot m} \ \leqq \ M_{Pa}=3.25 \ \mathrm{kN \cdot m} \end{split}\nonumber \end{equation} よって、OK
📌NOTE
$M_S = 2.48$は、前回記事の「鉛直支持力に対する安定照査」の4-3-6で算出しています。

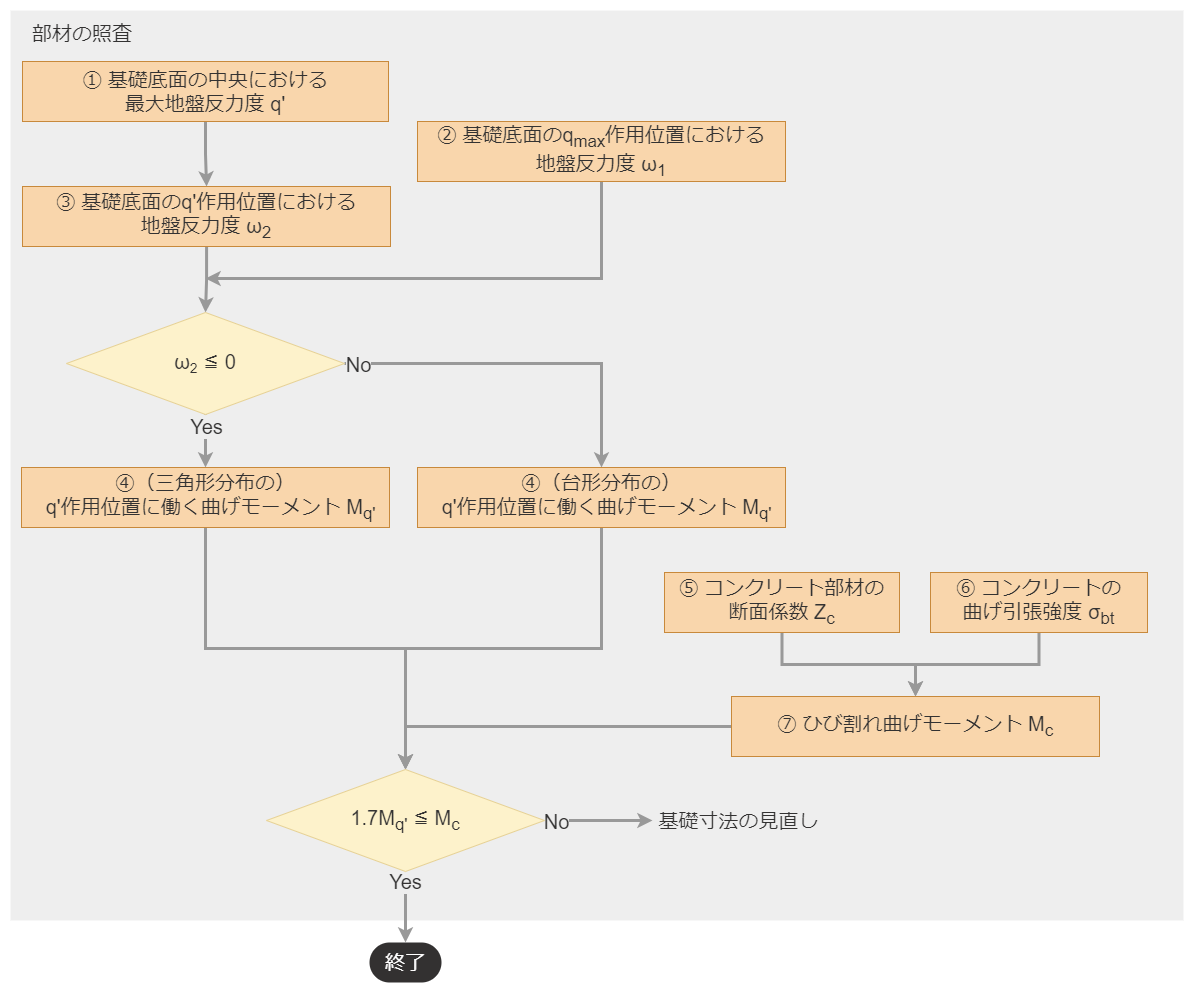
4-7. 部材の照査

照明灯の基礎における部材の照査とは、フーチングの部材に生じる応力度が許容応力度以下であることを照査します。

📌NOTE
無筋コンクリートの場合、照査の手順は下記のとおり。
  1. 「基礎底面の中央における最大地盤反力度 $q’$ 」を求める。
  2. 「基礎底面の $q_{max}$ 作用位置における地盤反力度 $\omega_1$ 」を求める。
  3. 「基礎底面の $q'$ 作用位置における地盤反力度 $\omega_2$ 」を求める。
  4. 地盤反力の分布形状を確認し、「 $q'$ 作用位置に働く曲げモーメント $M_{q'}$ 」を求める。
  5. 基礎寸法から、「コンクリート部材の断面係数 $Z_c$ 」を求める。
  6. コンクリートの設計基準強度から、「コンクリートの曲げ引張強度 $\sigma_{bt}$ 」を求める。
  7. $Z_c$ と $\sigma_{bt}$ から、「ひび割れ曲げモーメント $M_c$ 」を求める。
  8. $1.7 M_{q'} \ \leqq \ M_c$ を満足すれば、照査終了。

4-7-1. 基礎底面の中央における最大地盤反力度 q’

\begin{equation} \begin{split} q' &= q_{max} \left(1- \frac{B}{2 \cdot x}\right) \\[0.5em] &= 81.203 \left( 1- \frac{1.3}{2 \times 0.69} \right) \\[0.5em] &= 4.53 \ \mathrm{kN/m^2} \end{split}\label{q'} \end{equation}
📌NOTE
$q_{max}=81.203$は、前回記事の鉛直支持力に対する安定照査の4-3-10で算出しています。

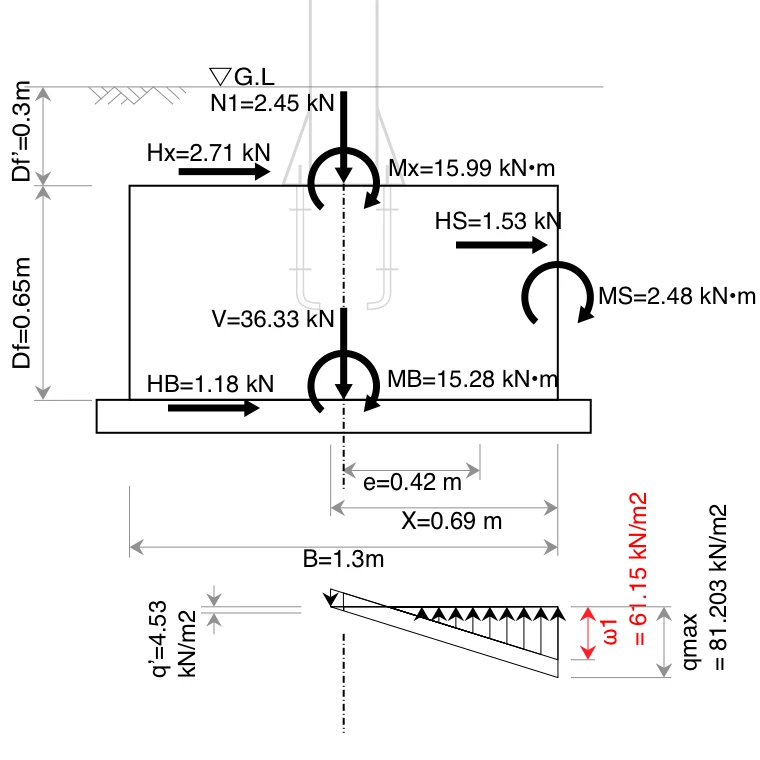
4-7-2. 基礎底面の qmax 作用位置における地盤反力度 ω1

\begin{equation} \begin{split} \omega_1 &= q_{max} - D_f \cdot \gamma_c - {D_f}' \cdot \gamma_s \\[0.5em] &= 81.203 - 0.65 \times 23 - 0.3 \times 17\\[0.5em] &= 61.15 \ \mathrm{kN/m^2} \end{split}\label{omega1} \end{equation}
📌NOTE
  • $\omega_1$は、$q_{max}$から、「コンクリート基礎の自重」と、「土被りの土の重量」を差し引いて、算出しています。
  • コンクリート基礎は「無筋」を想定して単位体積重量を$\gamma_c =23$とし、土は$\gamma_s =17$としています。

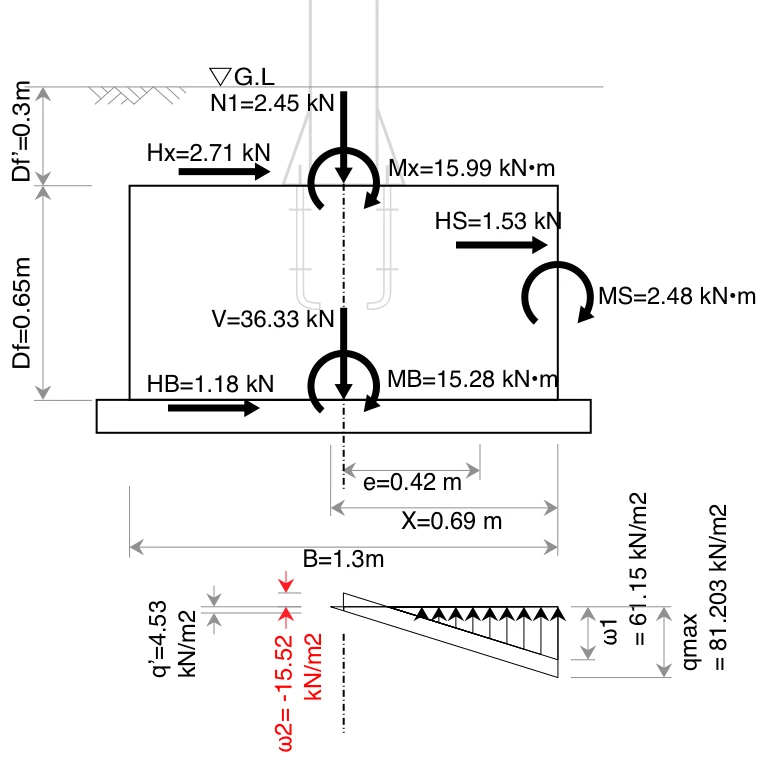
4-7-3. 基礎底面の q’ 作用位置における地盤反力度 ω2

\begin{equation} \begin{split} \omega_2 &= q' - D_f \cdot \gamma_c - {D_f}' \cdot \gamma_s \\[0.5em] &= 4.53 - 0.65 \times 23 - 0.3 \times 17\\[0.5em] &= -15.52 \ \mathrm{kN/m^2} \end{split}\label{omega2} \end{equation}

$\omega_2 \leqq 0$なので、三角分布

📌NOTE
  • $\omega_2 > 0$の場合は、台形分布となり次に算出する曲げモーメントの式が変わります。
  • 詳しくはR2道路標識構造便覧p.125,126をご覧ください。

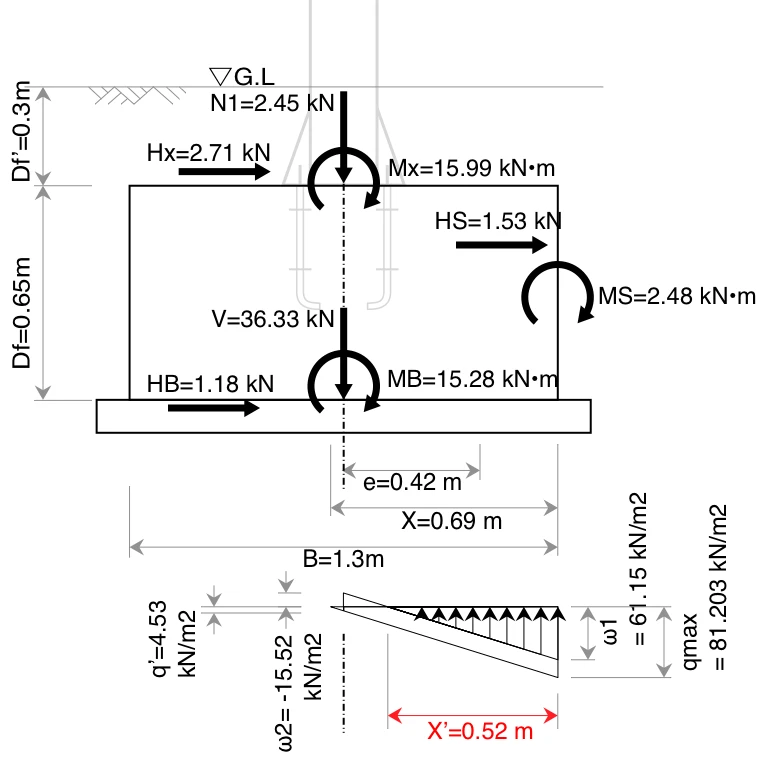
4-7-4. q’ 作用位置に働く曲げモーメント Mq’

$$ \begin{equation} \begin{split} M_{q'} &= \frac{B \cdot \omega_1 \cdot X'}{2} \cdot \left( \frac{B}{2} - \frac{X'}{3} \right) \\[0.5em] &= \frac{1.3 \times 61.15 \times 0.52}{2} \times \left( \frac{1.3}{2} - \frac{0.52}{3} \right) \\[0.5em] &= \frac{41.21}{2} \times 0.48 \\[0.5em] &= 9.83\ \mathrm{kN \cdot m} \end{split}\label{Mq} \end{equation} $$

ここで

  • $X'$：基礎自重と土被り重量を控除した底面反力の作用幅（m）
\begin{equation} \begin{split} X' &= \frac{B \cdot \omega_1}{2 \cdot ( \omega_1 - \omega_2 )} \\[0.5em] &= \frac{1.3 \times 61.15}{2 \times (61.15 -(-15.52))}\\[0.5em] &= \frac{79.50}{153.35}\\[0.5em] &= 0.52\ \mathrm{m} \end{split}\nonumber \end{equation}
📌NOTE
$X'$の式は、R2道路標識構造便覧p.125に記載されていますが、初版には誤植がありますので、日本道路協会のWebサイトで正誤表をご確認ください。

4-7-5. コンクリート部材の断面係数 Zc

$$ \begin{equation} \begin{split} Z_c &= \frac{L \cdot {D_f}^2}{6} \\[0.5em] &= \frac{1.3 \times 0.65^2}{6}\\[0.5em] &= \frac{0.55}{6}\\[0.5em] &= 0.092\ \mathrm{m^3} \end{split}\label{Zc} \end{equation} $$

4-7-6. コンクリートの曲げ引張強度 σbt

$$ \begin{equation} \begin{split} \sigma_{bt} &= 0.23 {\sigma_{ck}}^{2/3} \\[0.5em] &= 0.23 \times 18^{2/3}\\[0.5em] &= 1.58 \ \mathrm{N/mm^2}\\[0.5em] &= 1,580\ \mathrm{kN/m^2} \end{split}\label{sigmabt} \end{equation} $$

ここで

  • $\sigma_{ck}$：コンクリートの設計基準強度（N/mm²）
    • $\sigma_{ck} = 18\ \mathrm{N/mm^2}$

4-7-7. ひび割れ曲げモーメント Mc

式\eqref{Zc}、式\eqref{sigmabt}より

$$ \begin{equation} \begin{split} M_c &= Z_c \cdot \sigma_{bt} \\[0.5em] &= 0.092 \times 1,580 \\[0.5em] &= 144.61\ \mathrm{kN \cdot m} \end{split}\label{Mc} \end{equation} $$

4-7-8. 判定

式\eqref{Mq}、式\eqref{Mc}より

$$ \begin{equation} \begin{split} 1.7 M_{q'} &= 1.7 \times 9.83 \\[0.5em] &= 16.72 \ \leqq \ (M_c=144.61)\\ \end{split}\nonumber \end{equation} $$

よって、無筋コンクリートでOK

📌NOTE
  • R2道路標識構造便覧p.125では、「基礎の長さが3m以下」という条件があります。
  • 照明灯の基礎ならば、そこまで大きくはならないでしょう。

エクセルブック

計算を記載したエクセルブックは下記からダウンロードしてください。

DOWNLOAD

もし、間違いなどを見つけられた場合は、ご連絡いただけると幸いです。

📌NOTE
  • 近畿地方整備局の設計便覧（案）では、「鉛直支持」の照査のみを行い、「転倒」、「滑動」、「水平支持」、「部材」の照査を行っていませんが、やはり設計では考慮すべきでしょう。
  • 例えば、1,400×1,400×400の基礎寸法を照査すると、「鉛直支持」はOKとなりますが、「転倒」でNGとなります。
  • 基準書に従って設計してOKとなっても、現場の照明灯が転倒したのでは、設計としての意味がありません。