主働土圧係数
主働土圧係数とは?
主働土圧係数とは、擁壁背面にある土の水平力によって擁壁が前面方向へ動き始める時の、土の鉛直力に対する水平力の比率である。
土の鉛直力は、土の単位体積重量$\gamma_s$に土の深さ$H$を乗じることで計算できるので、これに主働土圧係数$K_A$を乗じることで、深さ$H$における水平力「主働土圧強度$p_A$」が算出できる。
計算式にすると次のとおり。
- $p_A$:主働土圧強度(kN/m²)
- $\gamma_s$:土の単位体積重量(kN/m³)
- $H$:土の深さ(m)
- $K_A$:主働土圧係数
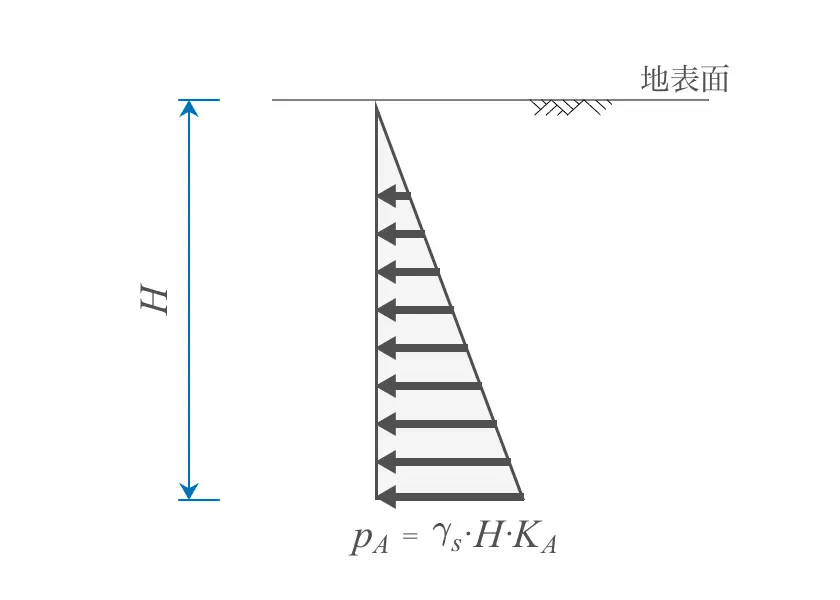
土圧は、深さ比例して増加するので、圧力分布は三角形になる。
このため、深さ$H$の主働土圧合力$P_A$は下式のとおりとなる。
このように、主働土圧係数は擁壁背面の主働土圧合力を算出することに用いる値でもある。
求め方
ランキンの土圧理論
条件として、
- 擁壁の背面が垂直
- 擁壁と土の摩擦を無視
であるとき、主働土圧係数は下式のとおりとなる。
ここに、
- $\phi$:内部摩擦角(°)
クーロンの土圧理論
ランキンの土圧理論を一般化したもので、主働土圧係数は下式のとおりとなる。
- $\phi$:内部摩擦角(°)
- $\alpha$:擁壁背面の壁面傾斜角(°)
- $\delta$:壁面摩擦角(°)
- $\beta$:地表面の傾斜角(°)
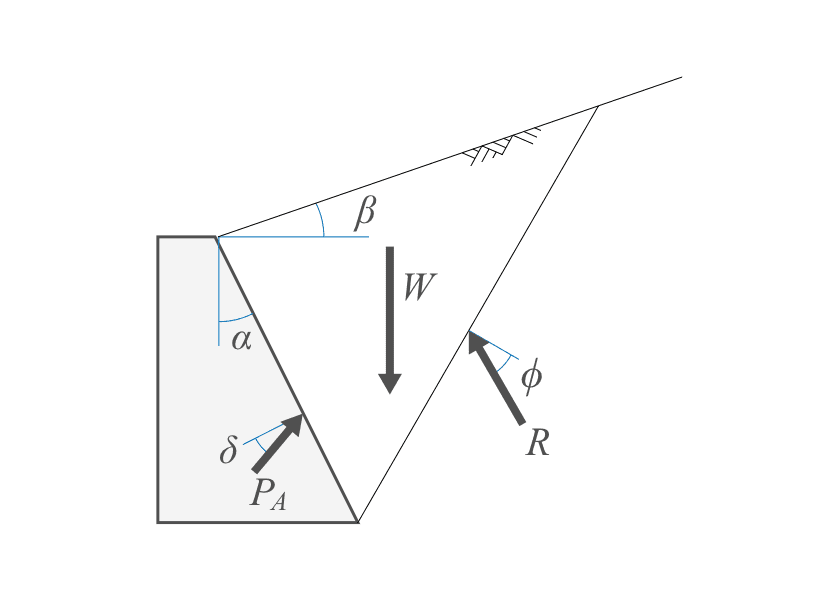
上式に、$\alpha=90$、$\delta=0$、$\beta=0$を代入すると、ランキンの土圧理論と同じ式になります。
このほか、もたれ擁壁の設計では、くさび型の土塊による主働土圧合力から、主働土圧係数を逆算する方法も用いられます。
詳しくは、下記の記事をご覧ください。
Excelでもたれ式擁壁(直接基礎)の設計計算 -岩盤、ガードレールC種-
この記事では、道路に設置される「もたれ式擁壁(直接基礎)」をエクセルで設計計算してみた結果をご紹介します。
構造計算における主働土圧係数の使い方
仮設土留め壁の設計においては、ランキンの土圧理論で主働土圧係数を算出し、主働土圧を求めます。
Excelで仮設土留め壁の設計計算 -自立式鋼矢板、砂質地盤-
この記事では、土木工事に用いられる仮設土留め壁「自立式鋼矢板」をエクセルで設計計算してみた結果をご紹介します。
重力式擁壁や、片持ばり式擁壁の設計においては、主働土圧を算出するために、クーロンの土圧理論による主働土圧係数を使います。ただし、下記の計算例では、あえて主働土圧係数を用いずに主働土圧を算出しています。
Excelで重力式擁壁(重要度1)の設計計算 -嵩上げ盛土-
この記事では、道路に設置される「重力式擁壁(重要度1)」をエクセルで設計計算してみた結果をご紹介します。