断面係数とは？

断面係数とは、曲げモーメントを受ける部材断面に発生する縁応力度を算出するために用いられる係数です。

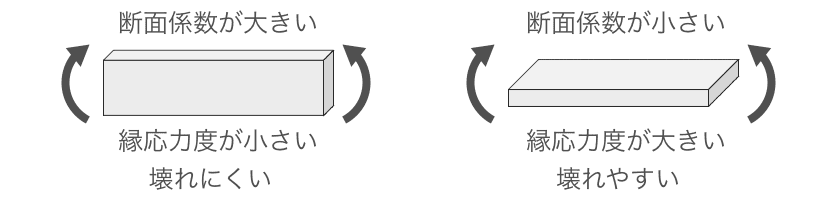
断面係数が大きいと、縁応力度が小さい（曲げモーメントに対して壊れにくい）断面ということになります。

図のとおり、断面係数の大きい部材は頑丈なことがイメージしやすいでしょう。

求め方

断面係数$Z$の計算方法は、次のとおりです。

一般式

断面係数$Z$は、次式で算出する。

$$ \begin{equation} \begin{split} Z =\frac{I}{y} \end{split}\nonumber \end{equation} $$

ここに、

  • $Z$：断面係数（m³）
  • $I$：断面二次モーメント（m⁴）
  • $y$：中立軸から縁までの距離（m）

長方形断面の場合

$$ \begin{equation} \begin{split} Z =\frac{b \cdot h^2}{6} \end{split}\nonumber \end{equation} $$
ここに、
  • $Z$：断面係数(m³)
  • $b$：幅(m)
  • $h$：高さ(m)

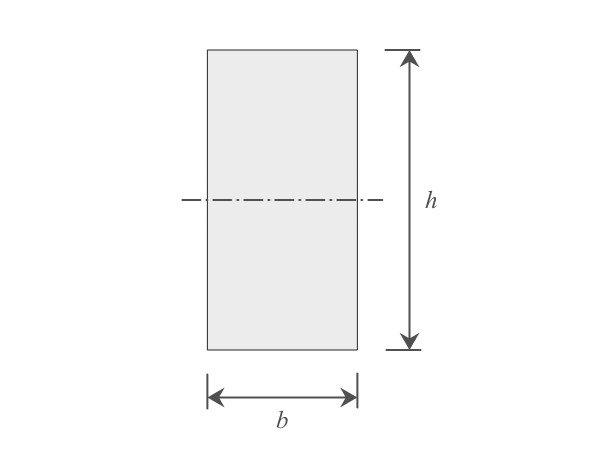
長方形断面の場合、断面係数の大きさは、幅に比例、高さの二乗に比例することが式から分かります。

このように、幅よりも高さ方向に寸法を大きくする方が、断面係数を大きくしやすく、部材が頑丈になるイメージが分かると思います。

使い方

変形係数は、擁壁や基礎などの無筋コンクリートにおける「部材の安全性の照査」や、親杭や鋼矢板などの鋼材における「曲げ応力度の照査」に用いられます。

部材に発生する最大曲げ応力度（縁応力度）は、次の式で計算します。

$$ \sigma_{max}=\frac{M}{Z} \nonumber $$

ここに

  • $\sigma_{max}$：部材に発生する最大曲げ応力度（N/mm2）
  • $M$：部材断面に作用する曲げモーメント（N・mm）
  • $Z$：断面係数（mm3/mm）

具体例は次のとおり。