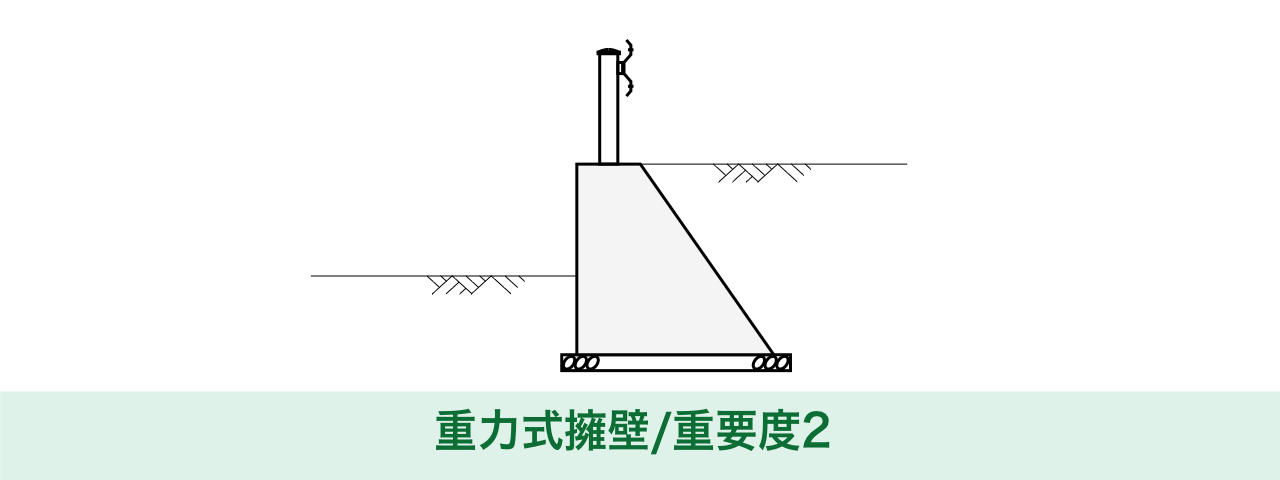
この記事では、道路に設置される「重力式擁壁(重要度2)」をエクセルで設計計算した結果をご紹介します。
設計の考え方とフローチャート
これから解説する内容は、社団法人日本道路協会が平成24年7月に発行した道路土工擁壁工指針(以下、H24道擁という。)に基づいています。
今回の紹介する設計プロセスは「擁壁上の盛り土は平面(嵩上げ盛土なし)、地下水なし、ガードレールC種、擁壁高さ5m以下」が適用範囲です。(H24道擁p27)
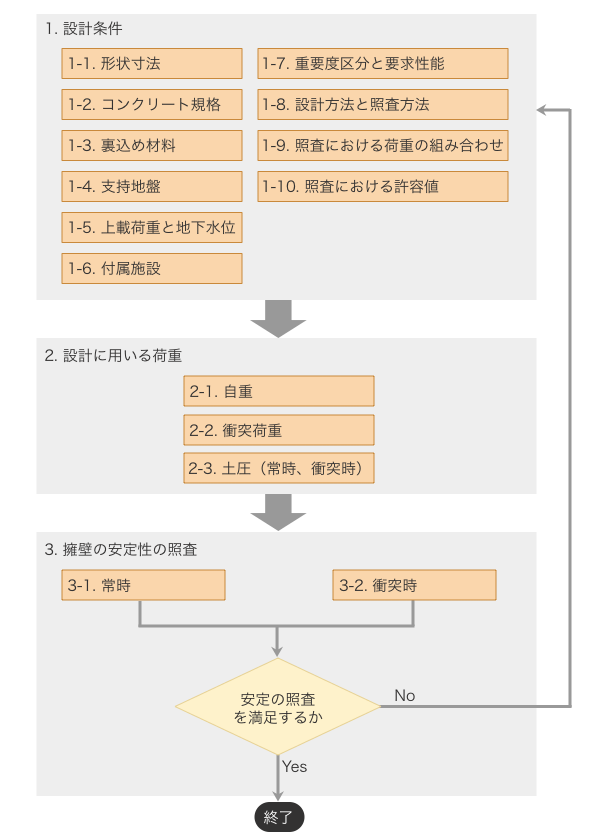
下記の画像は、設計のフローチャートです。
1. 設計条件
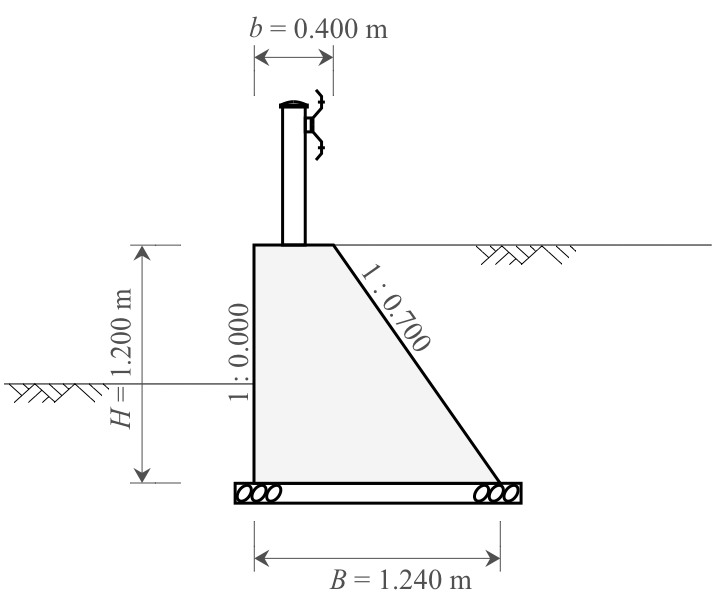
1-1. 形状寸法
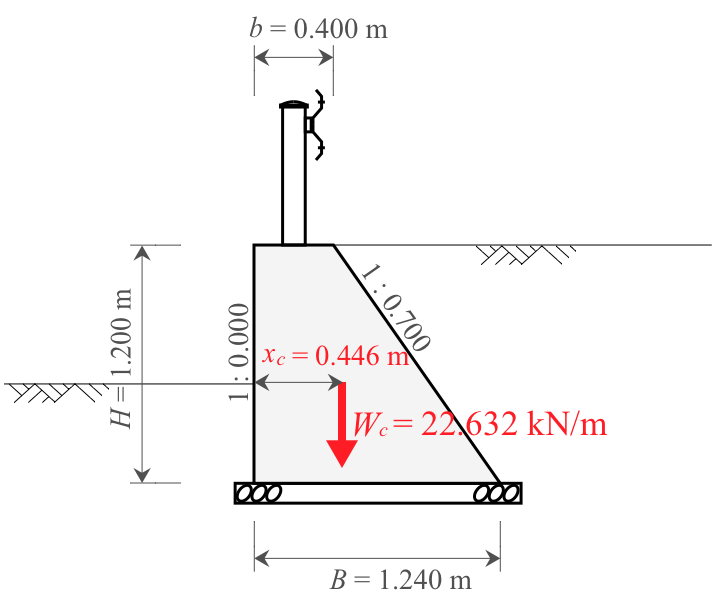
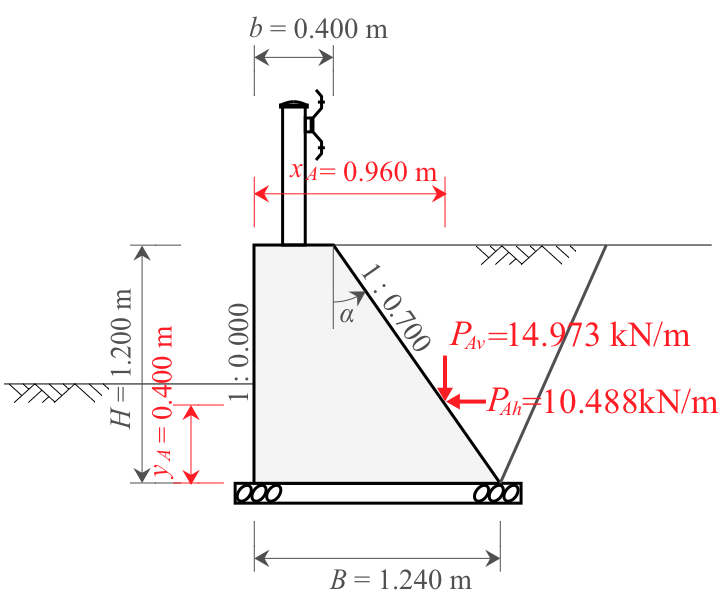
- 擁壁高:$H=1.200\ \mathrm{m}$
- 天端幅:$b=0.400\ \mathrm{m}$
- 底面幅:$B=1.240\ \mathrm{m}$
- 前面勾配:$n_1=0.000$
- 背面勾配:$n_2=0.700$
- 擁壁1ブロックの延長:$L=10\ \mathrm{m}$
1-2. コンクリート規格
- 設計基準強度:$\sigma_{ck}=18\ \mathrm{N/mm^2}$
- 単位体積重量:$\gamma_c=23\ \mathrm{kN/m^3}$(H24道擁p52)
1-3. 裏込め材料
- 裏込め土:砂質土
- せん断抵抗角:$\phi=30\ \mathrm{° }$(H24道擁p66)
- 単位体積重量:$\gamma_s=19\ \mathrm{kN/m^3}$(H24道擁p66)
- 粘着力:$c=0\ \mathrm{kN/m^2}$(H24道擁p66)
1-4. 支持地盤
- 土質:砂質地盤(中位なもの)
- 底面と地盤の摩擦係数:$\mu=0.6$(H24道擁p70)
- 付着力:$c_B=0\ \mathrm{kN/m^2}$(H24道擁p70)
- 許容鉛直支持力度(常時):$q_a=200\ \mathrm{kN/m^2}$(H24道擁p68,69)
- 許容鉛直支持力度(地震時・衝突時):$q_a=300\ \mathrm{kN/m^2}$(H24道擁p68,69,78)
- 中間層に軟弱な土層あるいは液状化が懸念されるゆるい砂質土層:なし
1-5. 上載荷重と地下水位
- 上載荷重:$q=10\ \mathrm{kN/m^2}$(H24道擁p53)
- 地下水位:なし
1-6. 付属施設
- 車両用防護柵:Gr-C種(H24道擁p213)
- 固定方法:砂詰め固定
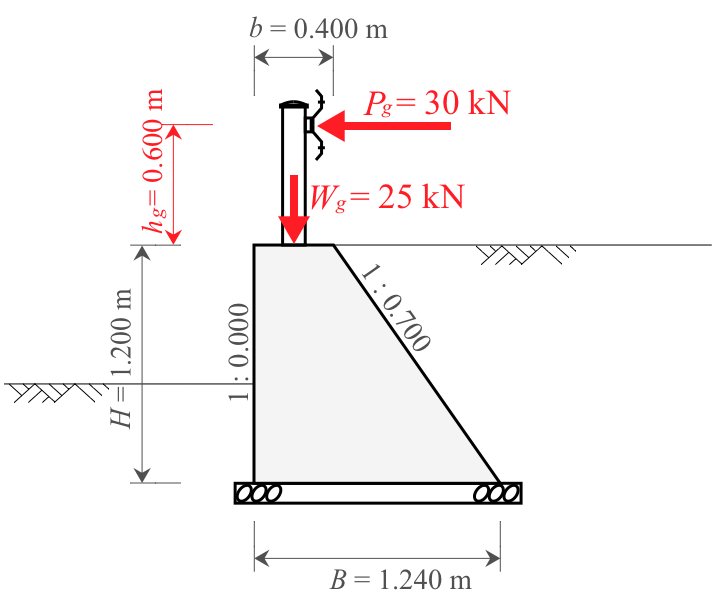
- 衝突荷重:$P_g=30\ \mathrm{kN}$(H24道擁p62)
- 擁壁天端から作用位置までの鉛直距離:$h_g=0.600\ \mathrm{m}$
- 衝突車両の前輪荷重:$W_g=25\ \mathrm{kN}$(H24道擁p63)
- 支柱中心部(作用位置)から天端前面までの距離:$b_g=0.200\ \mathrm{m}$
1-7. 重要度区分と要求性能
擁壁は、その重要度に応じて設計照査の方法(耐震設計の基本方針)を区分します。(H24道擁p42)
- 重要度1:万が一損傷すると交通機能に著しい影響を与える場合、あるいは隣接する施設に重大な影響を与える場合
- 重要度2:重要度1に該当するもの以外
この設計計算例では、「重要度2」とします。
| 📌NOTE |
- 重要度区分は「道路ネットワークとしての重要度」を定義しており、基本的な考え方として自治体が「緊急輸送道路」に設定している道路であれば、「重要度1」に指定します。
- 重要度の決定は、施設管理者の判断となりますが、う回路の有無など多方面からの検討に基づいて決定することが望ましいと言えます。
- 重要度の設定方法の一例としては、岐阜県Webサイトに掲載の「道路設計要領 第4-2章 4-2-7」が参考になります。
|
擁壁の要求性能とは、「擁壁の壊れにくさ」を定義しており、例えば「性能1」であれば、大震災後でも、健全性が保たれ道路を通行することができるほど壊れにくいということです。
要求性能は、3段階に区分されています
- 性能1:擁壁としての健全性を損なわない
- 性能2:損傷が限定的なものにとどまり、擁壁としての機能の回復が速やかに行い得る
- 性能3:損傷が擁壁として致命的とならない
この設計計算例では、重要度より要求性能を下記のとおり決定する。(H24道擁p44)
- 常時の作用:性能1
- 降雨の作用:性能1
- レベル1地震動の作用:性能2
- レベル2地震動の作用:性能3
| 📌NOTE |
- 公益社団法人日本道路協会のWebサイトに「道路土工構造物技術基準・同解説(平成29年3月)」出版後の道路土工指針等の取扱いについて記載されています。
- 同文書の3ページ目には、擁壁工に関する読み替えの例が記載されています。
- 内容は、「擁壁の要求性能」、「擁壁の限界状態」について読み替えの例となっています。
|
1-8. 設計方法と照査方法
設計方法は、「H24道擁の第5章に示した慣用的な設計方法(慣用法)」とする。
照査は、「擁壁の安定性」、「部材の安全性」、「排水工、付帯工」の3つに分けて行う。(H24道擁p88)
1-8-1. 擁壁の安定性
「擁壁の安定性」は、さらに「擁壁自体の安定性」、「背面盛土及び基礎地盤を含む全体としての安全性」に分けられる。
1-8-1-1. 擁壁自体の安定性の照査
「擁壁自体の安定性」について、H24道擁の第5章に示した慣用的な設計方法・施工方法に従えば、所要の性能を確保するとされており、例えば「常時の作用に対して性能1」を満足するとみなしてよいとされている。(H24道擁p88)
また、擁壁高$H \leqq 8\mathrm{m}$の場合、「常時の作用で照査」すれば、「レベル1地震動の作用に対して性能2」、「レベル2地震動の作用に対して性能3」を満足するとされている。(H24道擁p89)
よって、今回は「擁壁高$H \leqq 8\mathrm{m}$」かつ、「重要度2」であるため、「レベル1地震動の作用」と「レベル2地震動の作用」に対する安定性照査は不要となる。
さらに、今回は「地下水位がないこと」、および「排水工を適切に設置すること」を前提とし、「水圧の影響を考慮しない」こととなる。(H24道擁p55)
このため、「降雨の作用」については、通常、常時の作用における荷重の一項目として扱うが、今回はその荷重がないため、降雨に作用に対する照査を省略する。(H24道擁p49,88)
一方、擁壁天端に防護柵が設置されているため、「その他の作用(衝突時)で照査」が必要となる。
1-8-1-2. 背面盛土及び基礎地盤を含む全体としての安定性
「背面盛土及び基礎地盤を含む全体としての安定性」については、「1-4.支持地盤」に示したとおり、検討を要する層がないため、検討は不要となる。(H24道擁p111)
1-8-2. 部材の安全性
今回の重力式擁壁に「つま先版」が存在しない一般的な形状であるため、「部材の安全性の照査」は不要です。(H24道擁p158)
1-8-3. 排水工、付帯工
排水工は、上述の降雨による照査が不要となるようH24道擁p203の「5-9 排水工」に従い適切に設計するとこととする。
付帯工は、H24道擁p212の「5-10 付帯工」に従い設計することとする。
1-8-3. まとめ
まとめると、今回の設計例での設計方法と必要な照査は以下のとおり。
- 設計方法:H24道擁の第5章に示した慣用的な設計方法(慣用法)
- 照査方法
- 擁壁の安定性の照査
- 擁壁自体の安定性の照査
- 常時の作用で照査:要
- 降雨の作用で照査:不要
- レベル1地震動の$k_h$で照査:不要
- レベル2地震動の$k_h$で照査:不要
- その他の作用(衝突時)で照査:要
- 背面盛土及び基礎地盤を含む全体としての安定性の検討:不要
- 部材の安全性の照査:不要
- 排水工、付帯工:適切に設計する
1-9. 照査のおける荷重の組み合わせ
照査は、「常時」と「衝突時」のみ行うこととする。
衝突時には上載荷重を考慮しないため、下表のとおりの荷重の組み合わせとする。(H24道擁p51)
|
自重 |
上載荷重 |
土圧 |
衝突荷重 |
| 常時 |
有り |
有り |
有り |
- |
| 衝突時 |
有り |
- |
有り |
有り |
| 📌NOTE |
- 一般には、常時の作用に対しては「自重+載荷重+土圧」の組み合わせに加えて、「自重+土圧」の組み合わせについても設計を行うとされています。(H24道擁p51)
- これは、載荷重を無視すると、転倒に対する照査が危険側に推移することがあるからです。
- 実際にエクセルの入力項目のうち、「上載荷重」を「10」から「0」にしてみてください。
- 「3-1-2.転倒に対する照査」で算出される偏心距離$e$の値が「0.081」から「0.113」になり、許容値「0.207」以内であるものの、危険側になります。
- このため、本来は「自重+土圧」の組み合わせも照査の対象にするのが正しいのですが、エクセル上で簡単に確認できるため、省略しています。
|
1-10. 照査における許容値
照査に用いる許容値は以下のとおりとする。(許容鉛直支持力度は「1-4. 支持地盤」より再掲)
| 常時 | 衝突時 |
| 転倒に対する安定条件(H24道擁p118) | $\displaystyle |e| \leq \frac{B}{6}$ | $\displaystyle|e| \leq \frac{B}{3}$ |
| 滑動に対する許容安全率(H24道擁p113) | 1.5 | 1.2 |
| 許容鉛直支持力度(H24道擁p68,69,78) | 200 kN/m² | 300 kN/m² |
| 許容変位(H24道擁p110) | 省略 | 省略 |
| 📌NOTE |
- 衝突時の安全率や許容鉛直支持力度は、地震時の値を採用しています。
- 衝突荷重は「主荷重」ではなく「従荷重」とされています。(H24道擁p50)
- 従荷重とは、「必ずしも常時またはしばしば作用するとは限らないが、荷重の組合せにおいて必ず考慮しなければならない荷重」のことです。
- よって、衝突時は、常時の範疇に入らないと考えます。
- また、許容応力度の割増し係数は、衝突時と地震時が共に1.50である(H24道擁p78)ため、安全率や許容鉛直支持力度も地震時の値を採用するのが妥当と考えられます。
|
2. 設計に用いる荷重
2-1. 自重
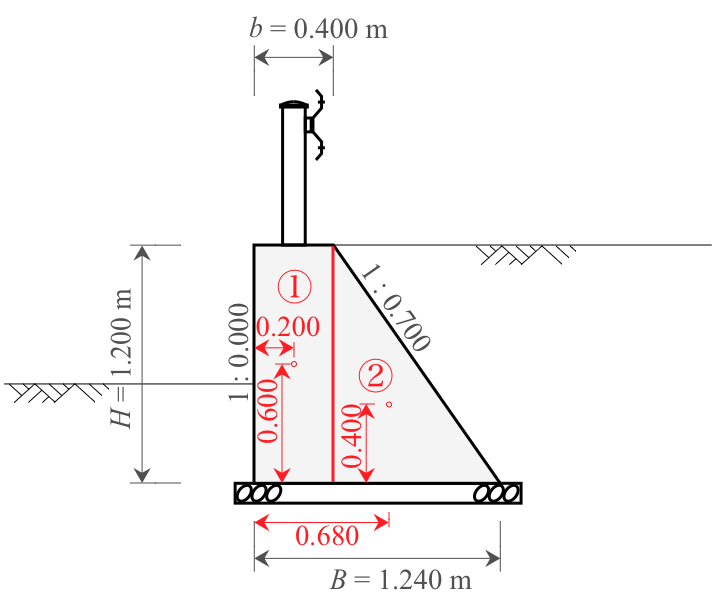
まず、自重の重心(水平方向の擁壁前面からの距離)を求めることとする。
擁壁断面を区分し、それぞれの面積、重心と擁壁前面・底面から距離、およびモーメントを下表のとおり求める。
| 区分 |
幅 |
高さ |
面積$A$ |
$x$ |
$y$ |
$Ax$ |
$Ay$ |
| ① |
0.400 |
1.200 |
0.480 |
0.200 |
0.600 |
0.096 |
0.288 |
| ② |
0.840 |
1.200 |
0.504 |
0.680 |
0.400 |
0.343 |
0.202 |
| Σ |
|
|
0.984 |
|
|
0.439 |
0.490 |
擁壁全体の重心位置(水平方向の擁壁前面からの距離)は、下式により求められる。
$$
\begin{equation}
\begin{split}
x_c &= \frac{\Sigma A x}{\Sigma A}\\[5px]
&= \frac{0.439}{0.984}\\[5px]
&= 0.446 \ \mathrm{m}
\end{split}\nonumber
\end{equation}
$$
自重$W_c$は、擁壁の断面積$A$に、コンクリートの単位体積重量$\gamma_c$を乗じて算出する。
$$
\begin{equation}
\begin{split}
W_c &= \Sigma A \cdot \gamma_c\\[5px]
&= 0.984 \cdot 23\\[5px]
&= 22.632 \ \mathrm{kN/m}
\end{split}\nonumber
\end{equation}
$$
2-2. 衝突荷重
衝突荷重は、水平力と鉛直力の2つに分けて算出する。
2-2-1. 水平力
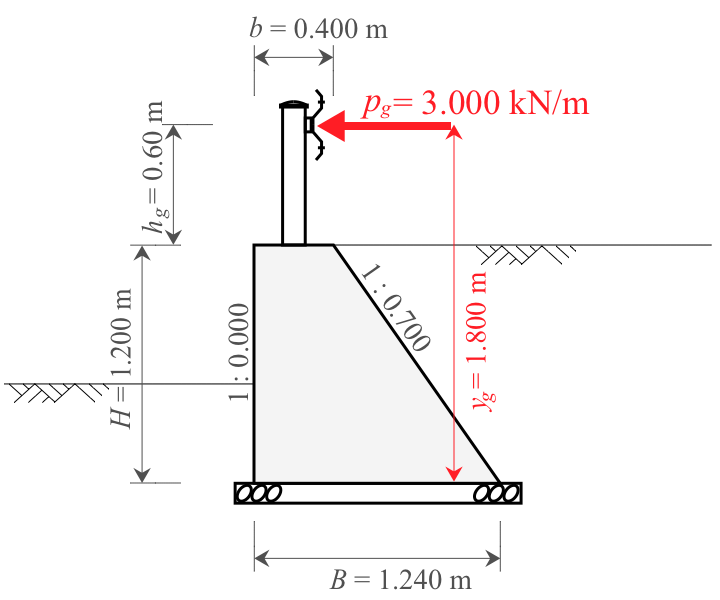
水平力は、擁壁天端に設置されたガードレールに車両が衝突した際の水平方向の荷重である。
この車両1台あたりの衝突荷重$P_g$を擁壁の1ブロック延長$L$で除して、単位幅あたりの衝突荷重$p_g$を算出する。
$$
\begin{equation}
\begin{split}
p_g &= \frac{P_g}{L}\\[5px]
&= \frac{30}{10}\\[5px]
&= 3.000 \ \mathrm{kN/m}
\end{split}\nonumber
\end{equation}
$$
次に、擁壁底面から作用位置までの鉛直距離$y_g$を算出する。「1. 設計条件」で定めたとおり、擁壁の高さ$H$に作用位置の高さ$h_g$を加える。
$$
\begin{equation}
\begin{split}
y_g &= H + h_g\\[5px]
&= 1.200 + 0.600\\[5px]
&= 1.800 \ \mathrm{m}
\end{split}\nonumber
\end{equation}
$$
2-2-2. 鉛直力
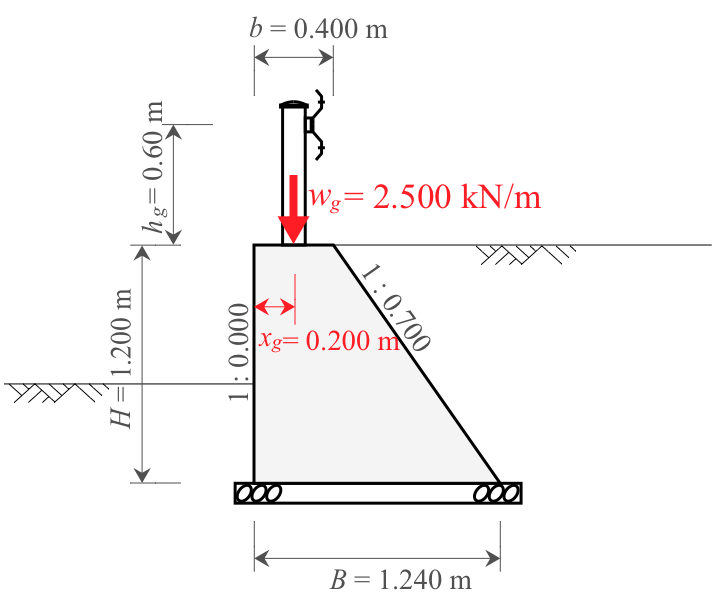
衝突荷重における鉛直力とは、車両がガードレールに衝突した際に、車両の前輪から擁壁にかかる輪荷重のことである。
鉛直力は、車両1台あたりの衝突車両の前輪荷重$W_g$を擁壁の1ブロック延長$L$で除して、単位幅あたりの衝突荷重$w_g$として算出する。
$$
\begin{equation}
\begin{split}
w_g &= \frac{W_g}{L}\\[5px]
&= \frac{25}{10}\\[5px]
&= 2.500 \ \mathrm{kN/m}
\end{split}\nonumber
\end{equation}
$$
次に、擁壁前面から作用位置までの水平距離$x_g$を算出する。
$$
\begin{equation}
\begin{split}
x_g &= b_g\\[5px]
&= 0.200 \ \mathrm{m}
\end{split}\nonumber
\end{equation}
$$
2-3. 土圧
2-3-1. 常時
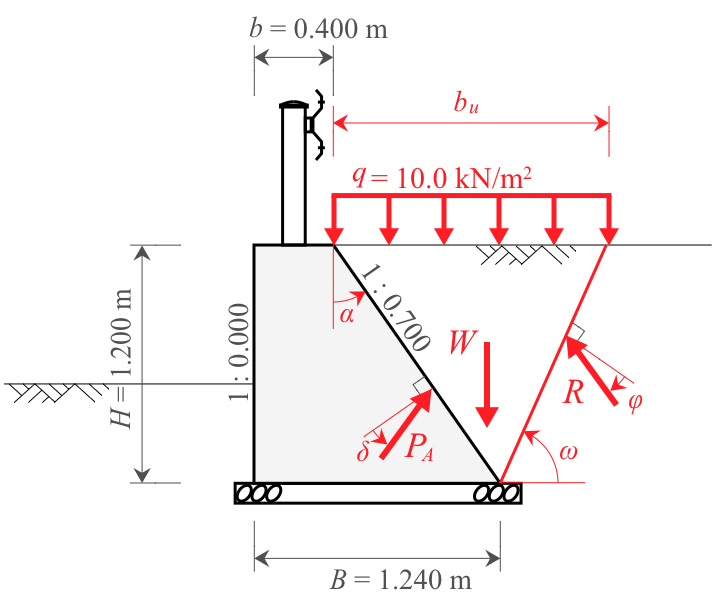
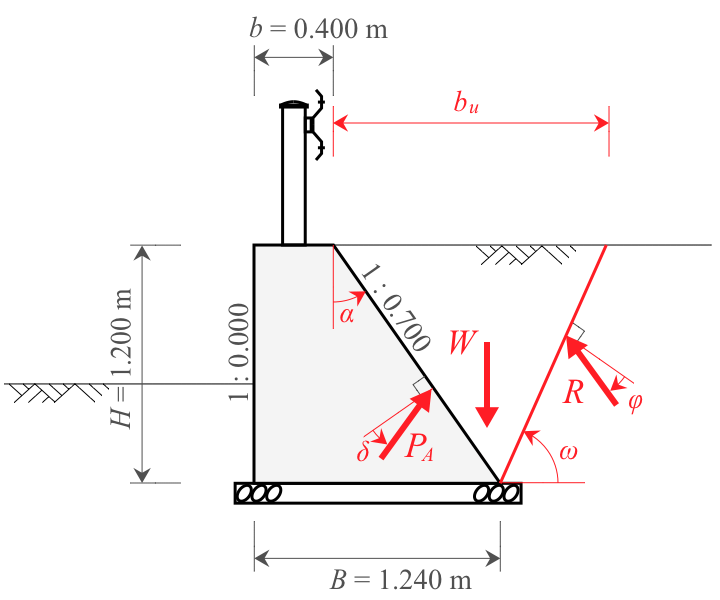
主働土圧は、試行くさび法によって算出する。(H24道擁p100)
擁壁上の盛土が平坦な場合(嵩上げ盛土がない場合)、主働土圧合力は下式で算出できる。(H24道擁p101)
$$
\begin{equation}
\begin{split}
P_A=\frac{W \cdot \sin(\omega - \phi)}{\cos(\omega - \phi - \alpha - \delta)}
\end{split}\nonumber
\end{equation}
$$
$$
\begin{equation}
\begin{split}
W = \frac{b_u \cdot H}{2}\cdot \gamma_s + q \cdot b_u
\end{split}\nonumber
\end{equation}
$$
$$
\begin{equation}
\begin{split}
b_u= (\tan \alpha + \frac{1}{\tan\omega})H
\end{split}\nonumber
\end{equation}
$$
ここに、
- $P_A$:主働土圧合力(kN/m)
- $W$:上載荷重を含んだ土くさび重量(kN/m)
- $b_u$:土塊上の上載荷重の作用幅(m)
- $\omega$:仮定したすべり面と水平面のなす角(° )
- $\phi$:裏込め土のせん断抵抗角(° )
- $\alpha$:壁背面と鉛直面のなす角(° ) $\alpha= \tan^{-1}n_2=\tan^{-1}0.700=34.990$
- $\delta$:壁面摩擦角(° )$\displaystyle \delta = \frac{2}{3}\cdot \phi = \frac{2}{3}\times 30 =20$(H24道擁p99)
| 📌NOTE |
- H24道擁p101には、上記の算出方法のほかに、主働土圧係数$K_A$を用いた算出方法が記載されています。
- 今回の計算例における設計条件では、主働土圧係数$K_A$を用いた算出方法が適用可能です。
- ただ、多くの土木系のソフトウェアでは、主働土圧係数$K_A$を用いた算出方法を採用していません。
- この記事は、技術者の学習用として視点を重視し、土木技術者が土木系ソフトウェアの出力結果を読み解けるよう配慮していますので、主働土圧係数$K_A$を用いた算出方法を採用しないこととしました。
|
よって、
$$
\begin{equation}
\begin{split}
P_A &=\frac{W \cdot \sin(\omega - \phi)}{\cos(\omega - \phi - \alpha - \delta)}\\[5px]
&=\frac{W \cdot \sin(\omega - 30)}{\cos(\omega - 30 - 34.990 - 20)}\\[5px]
&= \frac{W \cdot \sin(\omega - 30)}{\cos(\omega - 84.990)}
\end{split}\nonumber
\end{equation}
$$
$$
\begin{equation}
\begin{split}
W &= \frac{b_u \cdot H}{2} \cdot \gamma_s + q \cdot b_u\\[5px]
&= \frac{b_u \cdot 1.200}{2} \cdot 19 + 10 \cdot b_u\\[5px]
&= 21.400 \cdot b_u
\end{split}\nonumber
\end{equation}
$$
$$
\begin{equation}
\begin{split}
b_u &= (\tan \alpha + \frac{1}{\tan\omega})H \\[5px]
&= (\tan 34.990 + \frac{1}{\tan\omega})\cdot 1.200\\[5px]
&= (0.700 + \frac{1}{\tan\omega})\cdot 1.200
\end{split}\nonumber
\end{equation}
$$
すべり角$\omega$を変化させて、主働土圧合力$P_A$の最大値を求める。
上の式を用いて、表計算すると下記のとおりとなる。
すべり角
$\omega$
(° ) |
上載幅
$b_u$
(m) |
土くさび重量
$W$
(kN/m) |
主働土圧合力
$P_A$
(kN/m) |
| 61 |
1.505 |
32.209 |
18.158 |
| 62 |
1.478 |
31.629 |
18.207 |
| 63 |
1.451 |
31.059 |
18.243 |
| 64 |
1.425 |
30.500 |
18.267 |
| 65 |
1.400 |
29.949 |
18.280 |
| 66 |
1.374 |
29.408 |
18.281 |
| 67 |
1.349 |
28.875 |
18.271 |
よって、土圧合力が最大となるすべり角は
$$
\begin{equation}
\begin{split}
\omega = 66 \ \mathrm{° }
\end{split}\nonumber
\end{equation}
$$
その時の主働土圧合力は
$$
\begin{equation}
\begin{split}
P_A=18.281 \ \mathrm{kN/m}
\end{split}\nonumber
\end{equation}
$$
このとき、土圧合力の水平成分、鉛直成分、作用位置は次のとおりとなる。
水平成分
$$
\begin{equation}
\begin{split}
P_{Ah} &= P_A \cdot \cos(\alpha + \delta)\\[5px]
&= 18.281 \times \cos(34.990 + 20)\\[5px]
&= 10.488\ \mathrm{kN/m}
\end{split}\nonumber
\end{equation}
$$
鉛直成分
$$
\begin{equation}
\begin{split}
P_{Av} &= P_A \cdot \sin(\alpha + \delta)\\[5px]
&= 18.281 \times \sin(34.990 + 20)\\[5px]
&= 14.973\ \mathrm{kN/m}
\end{split}\nonumber
\end{equation}
$$
作用位置
$$
\begin{equation}
\begin{split}
y_A &= \frac{H}{3} \\[5px]
&= \frac{1.200}{3}\\[5px]
&= 0.400\ \mathrm{m}
\end{split}\nonumber
\end{equation}
$$
$$
\begin{equation}
\begin{split}
x_A &= B - \tan \alpha \times y_A \\[5px]
&= 1.200 - \tan 34.990 \times 0.400\\[5px]
&= 0.960\ \mathrm{m}
\end{split}\nonumber
\end{equation}
$$
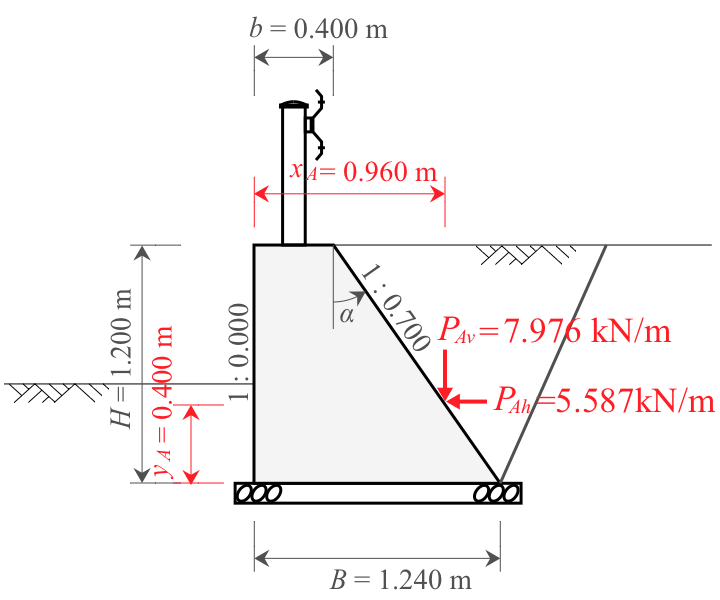
2-3-2. 衝突時
常時と同様に主働土圧は、試行くさび法によって算出する。
ただし、「1-9. 照査における荷重の組み合わせ」のとおり上載荷重$q=0$とする。
よって、
$$
\begin{equation}
\begin{split}
P_A &=\frac{W \cdot \sin(\omega - \phi)}{\cos(\omega - \phi - \alpha - \delta)}\\[5px]
&=\frac{W \cdot \sin(\omega - 30)}{\cos(\omega - 30 - 34.990 - 20)}\\[5px]
&= \frac{W \cdot \sin(\omega - 30)}{\cos(\omega - 84.990)}
\end{split}\nonumber
\end{equation}
$$
$$
\begin{equation}
\begin{split}
W &= \frac{b_u \cdot H}{2} \cdot \gamma_s + q \cdot b_u\\[5px]
&= \frac{b_u \cdot 1.200}{2} \cdot 19 + 0 \cdot b_u\\[5px]
&= 11.400 \cdot b_u
\end{split}\nonumber
\end{equation}
$$
$$
\begin{equation}
\begin{split}
b_u &= (\tan \alpha + \frac{1}{\tan\omega})H \\[5px]
&= (\tan 34.990 + \frac{1}{\tan\omega})\cdot 1.200\\[5px]
&= (0.700 + \frac{1}{\tan\omega})\cdot 1.200
\end{split}\nonumber
\end{equation}
$$
すべり角$\omega$を変化させて、主働土圧合力$P_A$の最大値を求める。
すべり角
$\omega$
(° ) |
上載幅
$b_u$
(m) |
土くさび重量
$W$
(kN/m) |
主働土圧合力
$P_A$
(kN/m) |
| 61 |
1.505 |
17.158 |
9.673 |
| 62 |
1.478 |
16.849 |
9.699 |
| 63 |
1.451 |
16.546 |
9.718 |
| 64 |
1.425 |
16.247 |
9.731 |
| 65 |
1.400 |
15.954 |
9.738 |
| 66 |
1.374 |
15.666 |
9.738 |
| 67 |
1.349 |
15.382 |
9.733 |
よって、土圧合力が最大となるすべり角は
$$
\begin{equation}
\begin{split}
\omega = 66 \ \mathrm{° }
\end{split}\nonumber
\end{equation}
$$
その時の主働土圧合力は
$$
\begin{equation}
\begin{split}
P_A=9.738 \ \mathrm{kN/m}
\end{split}\nonumber
\end{equation}
$$
なお、65° の土圧も9.738 kN/mですが、数字を丸めなければ、66° で土圧が最大になります。
このとき、土圧合力の水平成分、鉛直成分、作用位置は次のとおりとなる。
$$
\begin{equation}
\begin{split}
P_{Ah} &= P_A \cdot \cos(\alpha + \delta)\\[5px]
&= 9.738 \times \cos(34.990 + 20)\\[5px]
&= 5.587\ \mathrm{kN/m}
\end{split}\nonumber
\end{equation}
$$
$$
\begin{equation}
\begin{split}
P_{Av} &= P_A \cdot \sin(\alpha + \delta)\\[5px]
&= 9.738 \times \sin(34.990 + 20)\\[5px]
&= 7.976\ \mathrm{kN/m}
\end{split}\nonumber
\end{equation}
$$
$$
\begin{equation}
\begin{split}
y_A &= \frac{H}{3} \\[5px]
&= \frac{1.200}{3}\\[5px]
&= 0.400\ \mathrm{m}
\end{split}\nonumber
\end{equation}
$$
$$
\begin{equation}
\begin{split}
x_A &= B - \tan \alpha \times y_A \\[5px]
&= 1.200 - \tan 34.990 \times 0.400\\[5px]
&= 0.960\ \mathrm{m}
\end{split}\nonumber
\end{equation}
$$
3. 擁壁の安定性の照査
擁壁自体の安定性を照査する。
3-1. 常時
3-1-1. 作用力の集計
照査にあたり、作用力を集計します。
自重と土圧について、上記のとおり鉛直力と水平力をそれぞれ算出しましたので、作用位置までの距離を乗じて、モーメントを算出します。
| 鉛直力 | 水平力 | 作用位置(アーム長) | モーメント |
| $V$ | $H$ | $x$ | $y$ | $M_x = V \cdot x$ | $M_y = H \cdot y$ |
| (kN/m) | (kN/m) | (m) | (m) | (kN・m/m) | (kN・m/m) |
| 自重 | 22.632 | 0.000 | 0.446 | ― | 10.091 | 0.000 |
| 土圧 | 14.973 | 10.488 | 0.960 | 0.400 | 14.374 | 4.195 |
| 合計 | 37.605 | 10.488 | ― | ― | 24.465 | 4.195 |
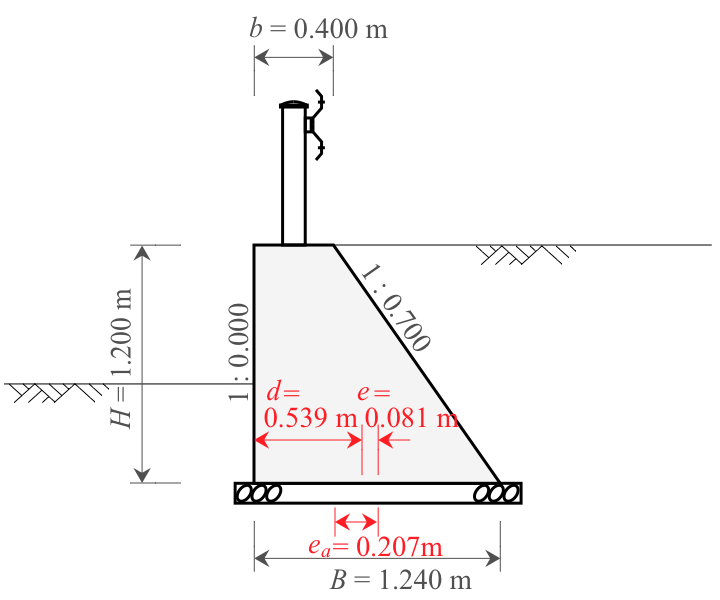
3-1-2. 転倒に対する照査
まず、許容偏心距離$e_a$を算出する。「1. 設計条件」で定めた「転倒に対する安定条件」より、次のとおり求められる。
$$
\begin{equation}
\begin{split}
e_a &= \frac{B}{6} \\[5px]
&= \frac{1.240}{6}\\[5px]
&= 0.207\ \mathrm{m}
\end{split}\nonumber
\end{equation}
$$
次に「作用力の合力位置$d$」を求める。
作用力の合力位置は、底面つま先から合力の作用点までの水平距離であり、次のとおり求められる。(H24道擁p117)
$$
\begin{equation}
\begin{split}
d &= \frac{\Sigma M_x - \Sigma M_y}{\Sigma V} \\[5px]
&= \frac{24.465 - 4.195}{37.605}\\[5px]
&= 0.539\ \mathrm{m}
\end{split}\nonumber
\end{equation}
$$
作用力の偏心距離$e$は、底面中心から作用力の合力位置まで距離であるため、次のとおり求められる。(H24道擁p118)
$$
\begin{equation}
\begin{split}
e &= \frac{B}{2} - d \\[5px]
&= \frac{1.240}{2} - 0.539\\[5px]
&= 0.081\ \mathrm{m}
\end{split}\nonumber
\end{equation}
$$
以上より、作用力の偏心距離$e=0.081$、許容偏心距離$e_a=0.207$なので、
$$
\begin{equation}
\begin{split}
e=0.081 \leqq 0.207 \ \ \bbox[2px, border: 2px solid]{\mathrm{OK}}
\end{split}\nonumber
\end{equation}
$$
よって、転倒に対しては安全である。
3-1-3. 滑動に対する照査
下式のとおり、滑動に対する抵抗力を滑動力で除して、安全率$F_s$を算出する。(H24道擁p113)
$$
\begin{equation}
\begin{split}
F_s = \frac{\Sigma V \cdot \mu + c_B \cdot B'}{\Sigma H}
\end{split}\nonumber
\end{equation}
$$
ここに、
よって、
$$
\begin{equation}
\begin{split}
F_s &= \frac{\Sigma V \cdot \mu + c_B \cdot B'}{\Sigma H} \\[5px]
&= \frac{37.605 \times 0.6 + 0 \times 1.078}{10.488}\\[5px]
&= 2.151
\end{split}\nonumber
\end{equation}
$$
「1. 設計条件」で定めたとおり、常時においては、滑動に対する許容安全率$F_{sa}=1.5$である。
$$
\begin{equation}
\begin{split}
F_s=2.151 \geqq 1.5 \ \ \bbox[2px, border: 2px solid]{\mathrm{OK}}
\end{split}\nonumber
\end{equation}
$$
よって、滑動に対しては安全である。
3-1-4. 支持に対する照査
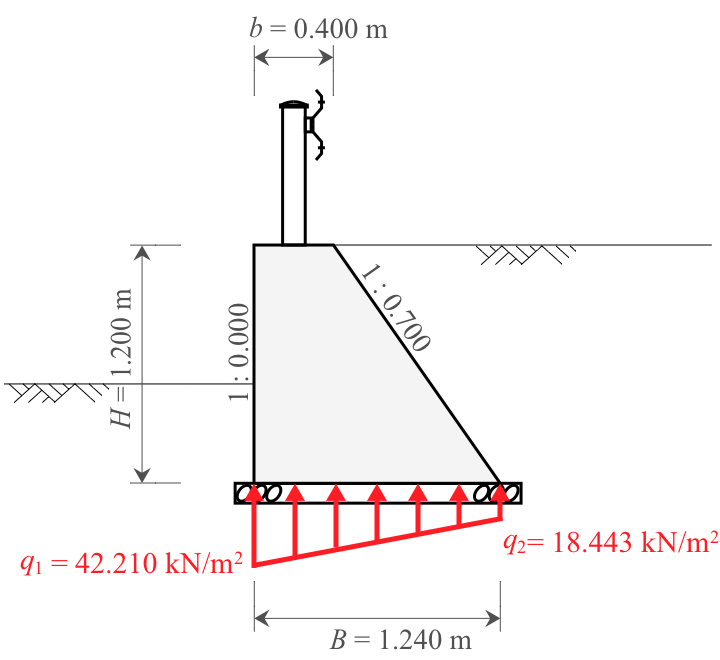
底面幅$B=1.240 \mathrm{m}$の中心から1/6の距離は、$1.240\times 1/6= 0.206 \mathrm{m}$である。
この値を2倍すると底面幅の1/3(ミドルサード)である。
作用力の偏心距離$e=0.081 \mathrm{m}$は、$0.206\mathrm{m}$以下であるため、作用力の合力位置は、底面幅中央の1/3(ミドルサード)内にある。
このとき、地盤反力は台形分布となり、その擁壁底面端部における地盤反力度$q_1$、$q_2$は下式で算出できる。(H24道擁p120)
$$
\begin{equation}
\begin{split}
q_1 &= \frac{\Sigma V}{B} \left( 1+ \frac{6 \cdot e}{B} \right) \\[5px]
&= \frac{37.605}{1.240} \left( 1+ \frac{6 \cdot 0.081}{1.240} \right) \\[5px]
&= 42.210\ \mathrm{kN/m^2}
\end{split}\nonumber
\end{equation}
$$
$$
\begin{equation}
\begin{split}
q_2 &= \frac{\Sigma V}{B} \left( 1- \frac{6 \cdot e}{B} \right) \\[5px]
&= \frac{37.605}{1.240} \left( 1- \frac{6 \cdot 0.081}{1.240} \right) \\[5px]
&= 18.443\ \mathrm{kN/m^2}
\end{split}\nonumber
\end{equation}
$$
「1. 設計条件」で定めたとおり、常時においては、許容鉛直支持力度$q_a=200$である。
$$
\begin{equation}
\begin{split}
q_1=42.210 \leqq 200 \ \ \bbox[2px, border: 2px solid]{\mathrm{OK}}\\[5px]
q_2=18.443 \leqq 200 \ \ \bbox[2px, border: 2px solid]{\mathrm{OK}}
\end{split}\nonumber
\end{equation}
$$
よって、支持に対しては安全である。
3-2. 衝突時
3-2-1. 作用力の集計
照査にあたり、作用力を集計します。
自重と土圧について、上記のとおり鉛直力と水平力をそれぞれ算出しましたので、それぞれに作用位置を乗じて、モーメントを算出します。
| 鉛直力 | 水平力 | 作用位置 | モーメント |
| $V$ | $H$ | $x$ | $y$ | $M_x = V \cdot x$ | $M_y = H \cdot y$ |
| (kN/m) | (kN/m) | (m) | (m) | (kN・m/m) | (kN・m/m) |
| 自重 | 22.632 | 0.000 | 0.446 | ― | 10.091 | 0.000 |
| 土圧 | 7.976 | 5.587 | 0.960 | 0.400 | 7.657 | 2.235 |
| 衝突荷重 | 2.500 | 3.000 | 0.200 | 1.800 | 0.500 | 5.400 |
合計 | 33.108 | 8.587 | ― | ― | 18.248 | 7.635 |
3-2-2. 転倒に対する照査
まず、許容偏心距離$e_a$を算出する。「1. 設計条件」で定めた「転倒に対する安定条件」より、次のとおり求められる。
$$
\begin{equation}
\begin{split}
e_a &= \frac{B}{3} \\[5px]
&= \frac{1.240}{3}\\[5px]
&= 0.413\ \mathrm{m}
\end{split}\nonumber
\end{equation}
$$
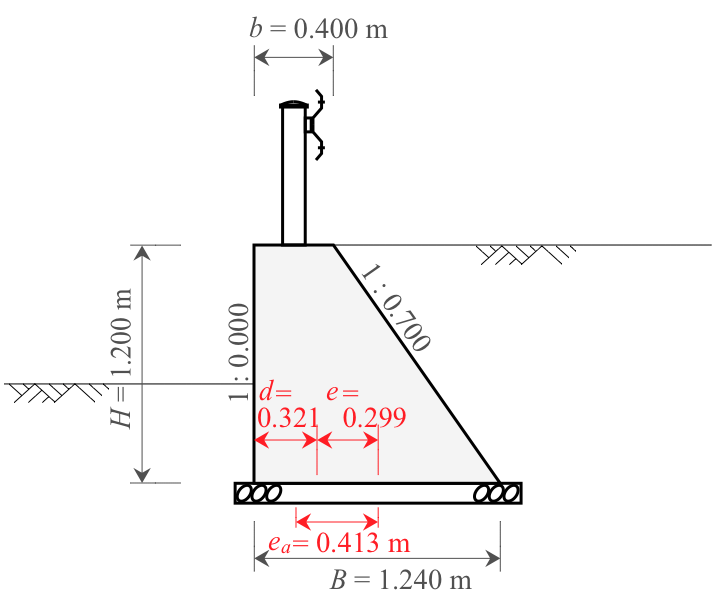
次に「作用力の合力位置$d$」を求める。
作用力の合力位置は、底面つま先から合力の作用点までの水平距離であり、次のとおり求められる。(H24道擁p117)
$$
\begin{equation}
\begin{split}
d &= \frac{\Sigma M_x - \Sigma M_y}{\Sigma V} \\[5px]
&= \frac{18.248 - 7.635}{33.108}\\[5px]
&= 0.321\ \mathrm{m}
\end{split}\nonumber
\end{equation}
$$
作用力の偏心距離$e$は、底面中心から作用力の合力位置まで距離であるため、次のとおり求められる。(H24道擁p118)
$$
\begin{equation}
\begin{split}
e &= \frac{B}{2} - d \\[5px]
&= \frac{1.240}{2} - 0.321\\[5px]
&= 0.299\ \mathrm{m}
\end{split}\nonumber
\end{equation}
$$
以上より、作用力の偏心距離$e=0.299$、許容偏心距離$e_a=0.413$なので、
$$
\begin{equation}
\begin{split}
e=0.299 \leqq 0.413 \ \ \bbox[2px, border: 2px solid]{\mathrm{OK}}
\end{split}\nonumber
\end{equation}
$$
よって、転倒に対しては安全である。
3-2-3. 滑動に対する照査
下式のとおり、滑動に対する抵抗力を滑動力で除して、安全率$F_s$を算出する。(H24道擁p113)
$$
\begin{equation}
\begin{split}
F_s = \frac{\Sigma V \cdot \mu + c_B \cdot B'}{\Sigma H}
\end{split}\nonumber
\end{equation}
$$
ここに、
よって、
$$
\begin{equation}
\begin{split}
F_s &= \frac{\Sigma V \cdot \mu + c_B \cdot B'}{\Sigma H} \\[5px]
&= \frac{33.108 \times 0.6 + 0 \times 0.641}{8.587}\\[5px]
&= 2.313
\end{split}\nonumber
\end{equation}
$$
「1. 設計条件」で定めたとおり、衝突時においては、滑動に対する許容安全率$F_{sa}=1.2$である。
$$
\begin{equation}
\begin{split}
F_s=2.313 \geqq 1.2 \ \ \bbox[2px, border: 2px solid]{\mathrm{OK}}
\end{split}\nonumber
\end{equation}
$$
よって、滑動に対しては安全である。
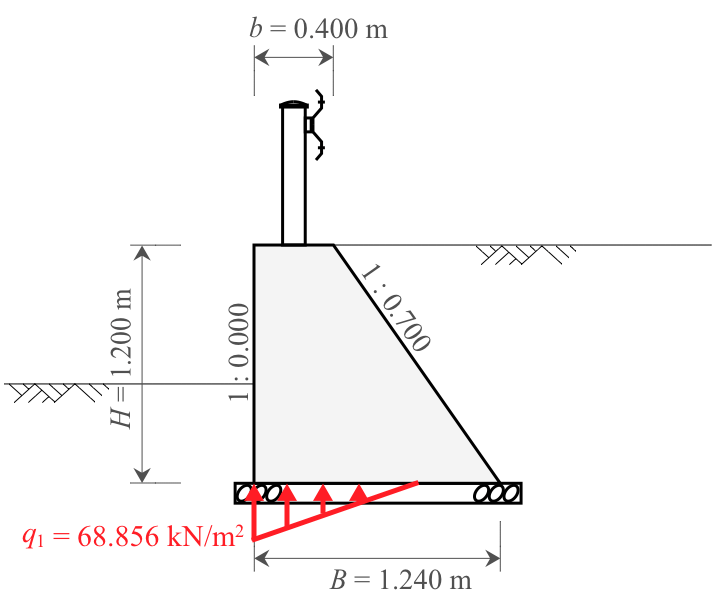
3-2-4. 支持に対する照査
底面幅$B=1.240 \mathrm{m}$の中心から1/6の距離は、$1.240\times 1/6= 0.206 \mathrm{m}$である。
この値を2倍すると底面幅の1/3(ミドルサード)である。
作用力の偏心距離$e=0.299 \mathrm{m}$は、$0.206\mathrm{m}$より大きいため、作用力の合力位置は、底面幅中央の1/3(ミドルサード)内にない。
ただし、底面幅$B=1.240 \mathrm{m}$の中心から1/3の距離は、$1.240\times 1/3= 0.413 \mathrm{m}$である。
作用力の偏心距離$e=0.299 \mathrm{m}$は、$0.413\mathrm{m}$以下であるため、作用力の合力位置は、底面幅の2/3内である。
このとき、地盤反力は三角分布となり、その擁壁端部位置での地盤反力度$q_1$は下式で算出できる。(H24道擁p120)
$$
\begin{equation}
\begin{split}
q_1 &= \frac{2 \Sigma V}{3d} \\[5px]
&= \frac{2 \times 33.108}{3 \times 0.321} \\[5px]
&= 68.856\ \mathrm{kN/m^2}
\end{split}\nonumber
\end{equation}
$$
「1. 設計条件」で定めたとおり、衝突時においては、許容鉛直支持力度$q_a=300$である。
$$
\begin{equation}
\begin{split}
q_1=68.856 \leqq 300 \ \ \bbox[2px, border: 2px solid]{\mathrm{OK}}\\[5px]
\end{split}\nonumber
\end{equation}
$$
よって、支持に対しては安全である。
エクセルブック
計算を記載したエクセルブックは下記からダウンロードしてください。
DOWNLOAD
シートに保護をかけていますが、パスワードは設定していません。
分かりにくかったり、間違いを見つけられた場合は、ご連絡いただけると幸いです。
なお、重要度1の場合は下記の記事で計算例を紹介しています。
Excelで重力式擁壁(重要度1)の設計計算 -嵩上げ盛土-
この記事では、道路に設定される「重力式擁壁(重要度1)」をエクセルで設計計算してみた結果をご紹介します。