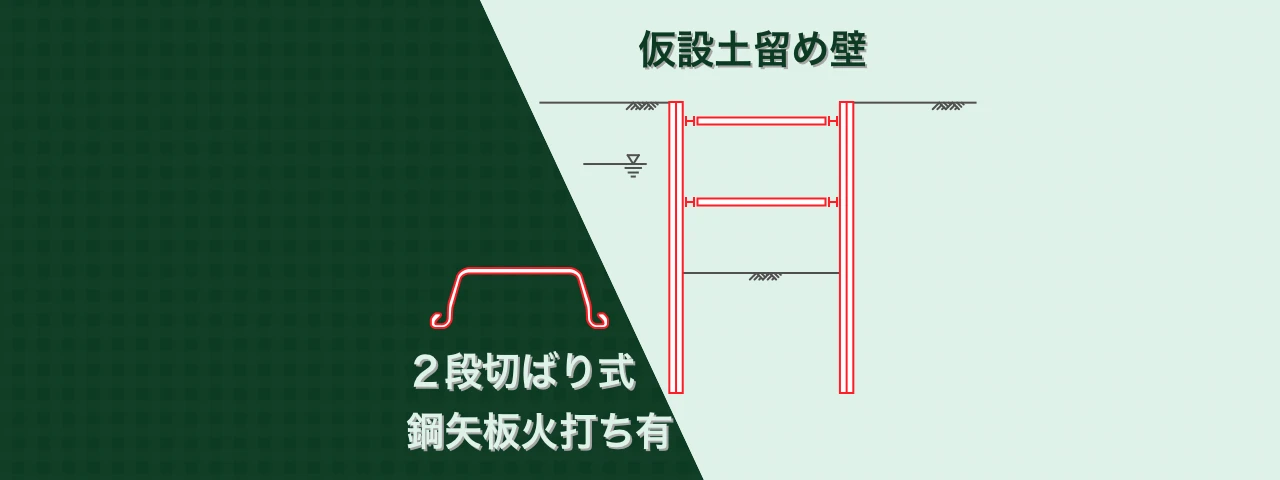
この記事では、土木工事に用いられる仮設土留め壁「２段切ばり式鋼矢板」をエクセルで設計計算してみた結果をご紹介します。

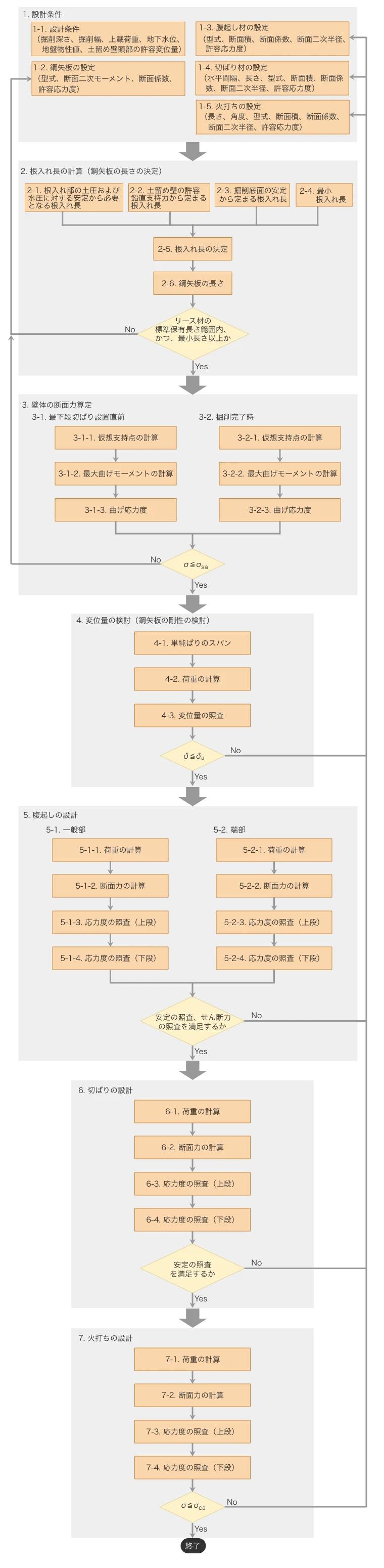
設計の考え方とフローチャート

設計の考え方は、社団法人日本道路協会が平成11年3月に発行した道路土工仮設構造物工指針（以下、H11道仮という。）に基づいています。

今回紹介する設計プロセスの適用範囲は「掘削深さH=3.0m超え10.0m以下、砂質地盤」です。（H11道仮p.28）

下記の画像は、設計のフローチャートです。クリックすると別ウィンドウで開きます。

📌NOTE
  • 仮設土留の設計フローは、H11道仮p.27にも掲載されていますが、切ばり式鋼矢板の設計に特化したフローを書いてみました。
  • これから解説する内容は、沖縄県のWebで公開されている「土木工事設計要領　第1編【共通編】（平成30年8月1日）」のp.2-98に記載の設計計算例を参考に、より詳細な設計計算例として作成したものとなっています。
  • 上記の沖縄県の資料には、計算ミスも含まれていたため、ここでは、それを修正しています。

1. 設計条件

1-1. 設計条件の設定

1-1-1. 掘削寸法・荷重・地下水位

  • 掘削深さ $H=7.0\ \mathrm{m}$
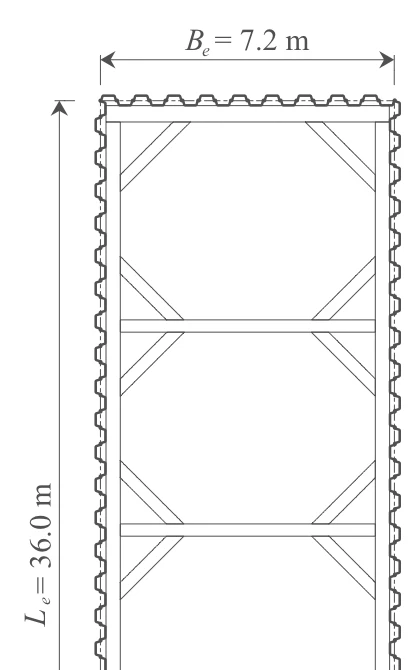
  • 掘削長さ（長辺） $L_e=36.0\ \mathrm{m}$
  • 掘削幅（短辺） $B_e=7.2\ \mathrm{m}$
  • 上載荷重 $q=10.0\ \mathrm{kN/m^2}$
  • 地表面から地下水位までの深さ $G.L.=-2.5\ \mathrm{m}$

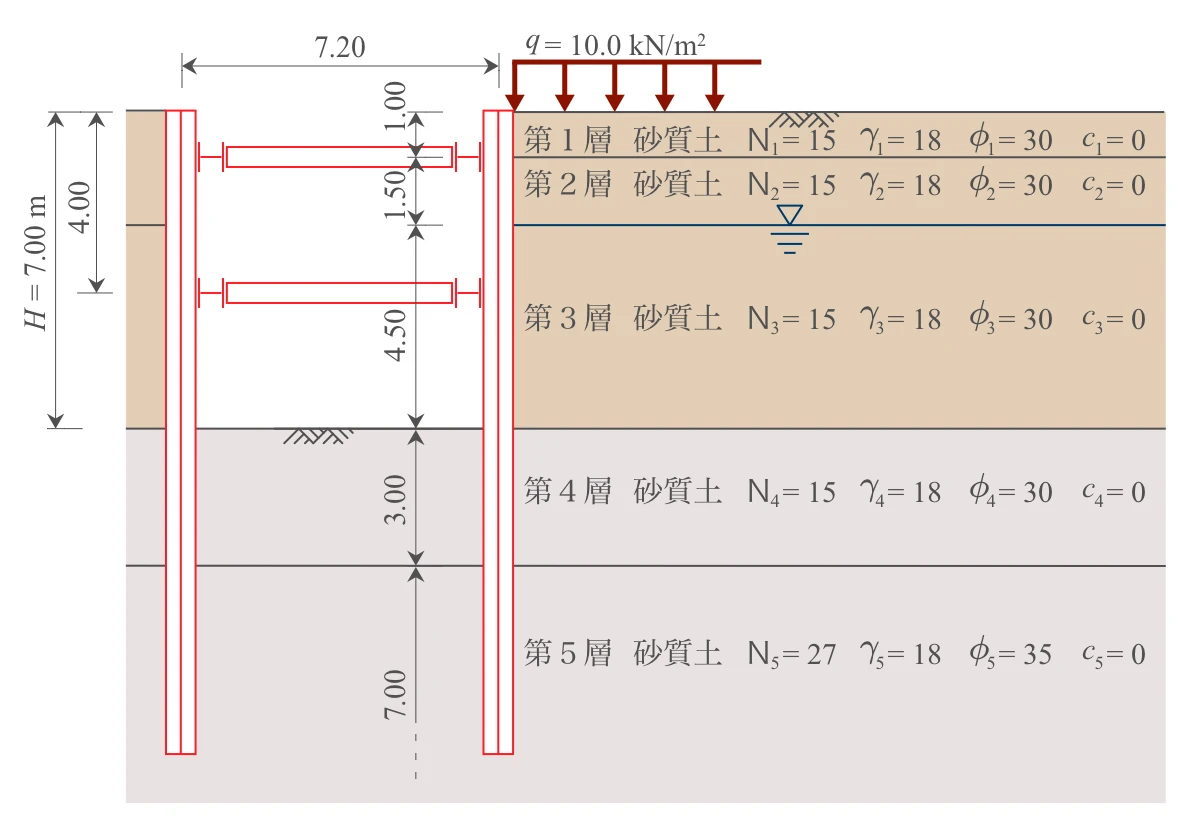
1-1-2. 地盤物性値

地盤の各数値を表にすると下記のとおりです。

層厚
$h$
(m)		 土質 地下水

(m)		 N値 単位体積重量
$\gamma$
(kN/m³)		 水中単位重量
$\gamma\ ^\prime$
(kN/m³)		 せん断抵抗角
$\phi$
(度)		 粘着力
$c$
(kN/m²)
1層 1.00 砂質土 － 15 18 － 30 0
2層 1.50 砂質土 － 15 18 － 30 0
3層 4.50 砂質土 4.50 15 18 9 30 0
掘削$\sum$ 7.00 4.50
4層 3.00 砂質土 3.00 15 18 9 30 0
5層 7.00 砂質土 7.00 27 18 9 35 0

1-1-3. 土留め壁頭部の許容変位量

土留め壁頭部の許容変位量は、$\delta_a =\textcolor{red}{0.30}\ \mathrm{m}$とします。（H11道仮p.94）

1-2. 鋼矢板の設定

設計条件として、鋼矢板の型式を「仮に」設定します。今回は、「$\mathrm{I}\hspace{-1.6pt}\mathrm{I}\hspace{-1.6pt}\mathrm{I}$型」にします。

  • 型式：$\mathrm{I}\hspace{-1.6pt}\mathrm{I}\hspace{-1.6pt}\mathrm{I}$型
  • 断面二次モーメント $I= 16,800\ \mathrm{cm^4/m}$
  • 断面係数 $Z= 1,340\ \mathrm{cm^3/m}$
  • 鋼矢板の許容応力度 $\sigma_{sa}= 270\ \mathrm{N/mm^2}$ （H11道仮p.48より）
  • ヤング係数 $E = 200,000\ \mathrm{N/mm^2}$ （H11道仮p.46より）
  • $h = 100\ \mathrm{mm}$ （H11道仮p.320より）
  • 断面二次モーメントの有効率（断面力、変位の計算）：$45$% （H11道仮p.107）
  • 断面係数の有効率（応力度の計算）：$60$% （H11道仮p.109）

後述する「2. 根入れ長の計算」、「3. 壁体の断面力算定」のいずれかで「NG」となった場合は、鋼矢板の設定（または、腹起し材の設定、切ばり材の設定、火打ちの設定）を見直すことになります。（フローチャート参照）

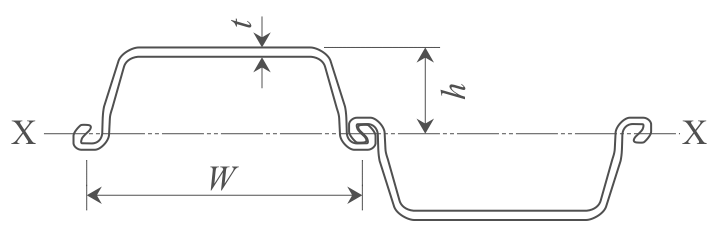
H11道路土工仮設構造物工指針p.320には、鋼矢板の型式が記載されています。設計に必要なところだけ抜粋して表にすると次のとおりです。

$W$
(mm)		 $h$
(mm)		 $t$
(mm)		 断面二次モーメント
(cm⁴/m)		 断面係数
(cm³/m)
$\mathrm{I}\hspace{-1.2pt}\mathrm{I}$型 400 100 10.5 8,740 874
$\mathrm{I}\hspace{-1.6pt}\mathrm{I}\hspace{-1.6pt}\mathrm{I}$型 400 125 13.0 16,800 1,340
400 130 13.0 17,400 1,340
$\mathrm{I}\hspace{-1.2pt}\mathrm{V}$型 400 170 15.5 38,600 2,270
$\mathrm{V_L}$型 500 200 24,3 63,000 3,150

このうち、「$\mathrm{I}\hspace{-1.2pt}\mathrm{I}$型」と「$\mathrm{I}\hspace{-1.6pt}\mathrm{I}\hspace{-1.6pt}\mathrm{I}$型のh=130」と「$\mathrm{V_L}$型」は、リース材として取り扱われていない地域があります。設計の際はその地域の実情にあわせて採用の可否を判断するべきでしょう。

📌NOTE
  • 鋼矢板の許容応力度については、H11道路土工仮設構造物工指針に掲載の値と、土木工事仮設計画ガイドブックに掲載の値とが異なっていますので、注意しましょう。
  • 有効率についての解説は、一般社団法人鋼管杭・鋼矢板技術協会の発行資料「鋼矢板Q&A」の「Q6.7 鋼矢板の継手効率とは？」が分かりやすいと思います。

1-3. 腹起し材の設定

腹起し材は、上段と下段の２段であり、一般部と端部をそれぞれ計算および照査する。 このため、本計算例では下記のとおり設定する。
  • 上段の位置　$G.L.=-1.0\ \mathrm{m}$
  • 下段の位置　$G.L.=-4.0\ \mathrm{m}$
  • 一般部　上段　H-350　１本
  • 一般部　下段　H-350　１本
  • 端部　　上段　H-400　１本
  • 端部　　下段　H-350　２本

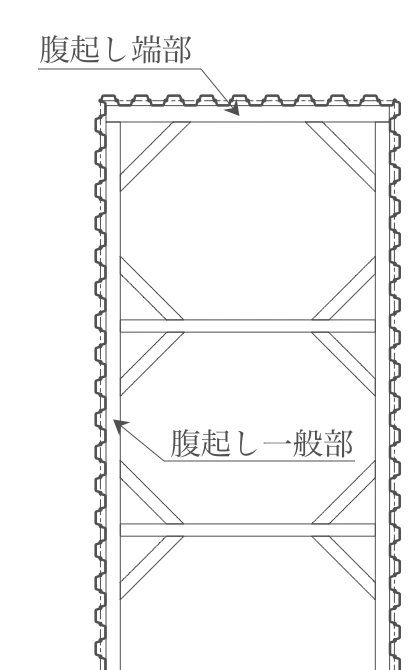
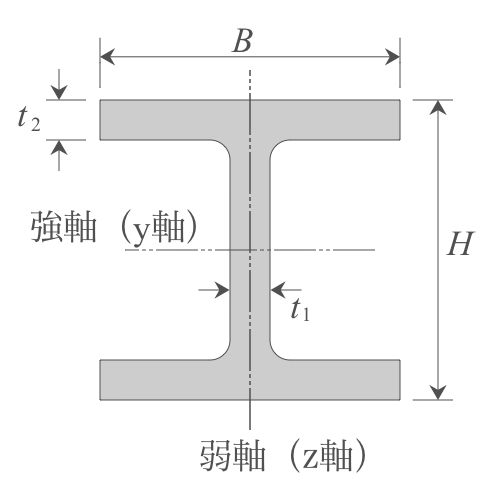
なお、H11道路土工仮設構造物工指針p.320には、Ｈ型鋼の型式が記載されています。設計に必要なところだけ抜粋して表にすると次のとおりです。

高さ
$H$
(mm)		 幅
$B$
(mm)		 ウェブ厚
$t_1$
(mm)		 フランジ厚
$t_2$
(mm)		 断面積
$A$
(cm²)		 断面二次半径
$r_y$
(cm⁴/m)
$r_y$
(cm⁴/m)		 断面係数
$Z$
(cm³/m)
H-200 200 200 8 12 51.53 8.43 4.22 366
H-250 250 250 9 14 78.18 10.60 6.05 708
H-300 300 300 10 15 104.80 12.90 7.51 1,150
H-350 350 350 12 19 154.90 15.10 8.99 2,000
H-400 400 400 13 21 197.70 17.30 10.10 2,950
鋼材の許容応力度は、以下の通りです。
  • 曲げ引張の許容応力度 $\sigma_{sa}= 210\ \mathrm{N/mm^2}$
  • せん断の許容応力度 $\tau_a= 120\ \mathrm{N/mm^2}$
📌NOTE
  • 曲げ引張の許容応力度を上記で示していますが、この計算例のプロセスでは使用されません。
  • ただし、後述のとおり同じ値が「局部座屈を考慮しない許容曲げ圧縮応力度の上限値」および「圧縮応力を受ける自由突出板の局部座屈に対する許容応力度」として、H11道仮p.51に記載されており、それらは、計算プロセスに登場します

1-4. 切ばり材の設定

切ばり材も腹起し材と同様、上段と下段の２段であり、それぞれ計算および照査する。 このため、本計算例では下記のとおり設定する。
  • 水平間隔　$B=5.00\ \mathrm{m}$
  • 長さ　$L=6.30\ \mathrm{m}$
  • 上段　H-300
  • 下段　H-300

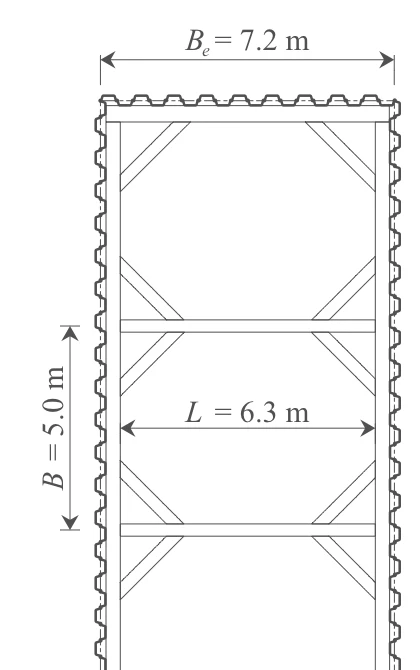
ここで、長さ$L$は、掘削幅（短辺）$B_e=7.2\ \mathrm{m}$と、鋼矢板の$h=100\ \mathrm{mm}$、腹起し材（一般部）の高さ$H=350\ \mathrm{mm}$より、次のとおり計算された値となっています。

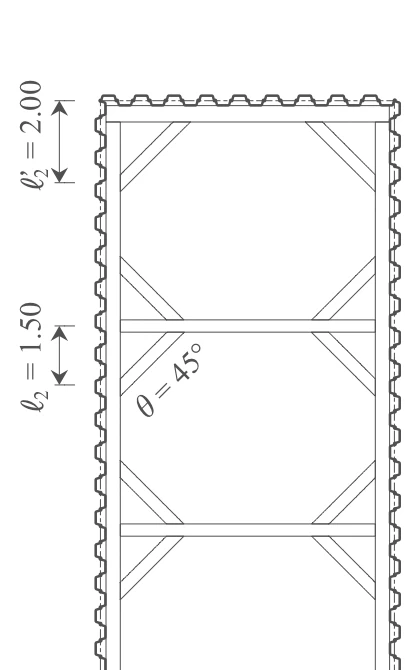
$$ \begin{equation} \begin{split} L &=B_e - 2 \cdot \frac{h}{1000} - 2 \cdot \frac{H}{1000} \\[5px] &=7.2 - 2 \cdot \frac{100}{1000} - 2 \cdot \frac{350}{1000} \\[5px] &=6.30 \end{split}\nonumber \end{equation} $$

1-5. 火打ちの設定

火打ちも腹起し材と同様、上段と下段の２段であり、それぞれ計算および照査する。 このため、本計算例では下記のとおり設定する。
  • 腹起し方向の幅　$ℓ_2=1.50\ \mathrm{m}$
  • 腹起し方向の幅（端部）　$ℓ_2'=2.00\ \mathrm{m}$
  • 角度　$\theta=45\ \mathrm{^\circ}$
  • H-300

2. 根入れ長の計算（鋼矢板の長さの決定）

2-1. 根入れ部の土圧および水圧に対する安定から必要となる根入れ長

根入れ長は、「掘削完了時」および「最下段切ばり設置直前」の両者において、それぞれつり合い深さの1.2倍とする。（H11道仮p.87）

つり合い深さ$ℓ_0$は、極限平衡法を用いて計算する。

2-1-1. 最下段切ばり設置直前

最下段設置時の余掘り量は「1m」とする。（H11道仮p.65）

よって、最下段（２段目）切ばり設置直前の掘削深さは、

$$ \begin{equation} \begin{split} GL &= - 4.0 - 1.0 \\[5px] &= - 5.0\ \mathrm{m} \end{split}\nonumber \end{equation} $$

となる。

(1) 主働土圧

主働土圧は次の式で求めます。（H11道仮p.35）

$$ \begin{align} p_a & =K_a\ (\sum\gamma\ h+q)-2c\sqrt{K_a}\nonumber \\ K_a & =\tan^2\left(45^\circ \ – \ \frac{\phi}{2}\right)\nonumber \end{align} $$

ここに、

  • $p_a$：主働土圧（kN/m²）
  • $K_a$：主働土圧係数
  • $\sum \gamma\ h$：着目点における地盤の有効土かぶり圧（kN/m²）
  • $\gamma$：各層の土の湿潤単位体積重量（kN/m³）
    • ただし、地下水位以下では水中単位体積重量 $\gamma\ ^\prime$ とする。
  • $h$：着目点までの各層の層厚（m）
  • $q$：地表面までの上載荷重（kN/m²）
  • $c$：土の粘着力（kN/m²）
  • $\phi$：土のせん断抵抗角（度）

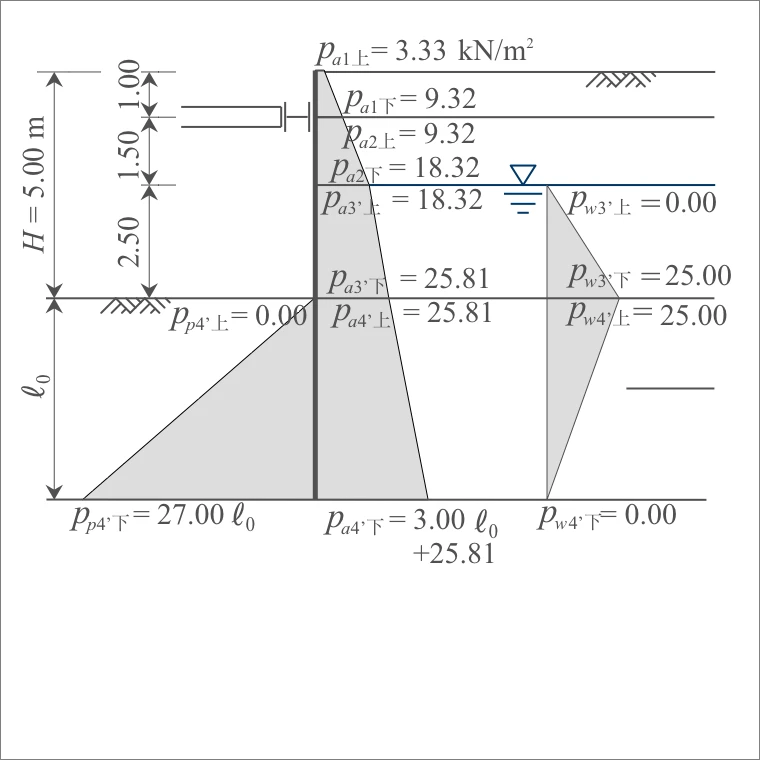
以上をもとに、掘削部の各層の主働土圧を表計算すると次のとおり。

層厚
$h$
(m)		 土質 主働土圧係数
$K_a$
$\gamma$
(kN/m³)
$\sum \gamma \ h+q$
(kN/m²)		 主働土圧
$p_a$
(kN/m²)
1層 1.00 砂質 0.333 18 10.00
28.00		 $p_{a1上}=$ 3.33
$p_{a1下}=$ 9.32
2層 1.50 砂質 0.333 18 28.00
55.00		 $p_{a2上}=$ 9.32
$p_{a2下}=$ 18.32
3'層 2.50 砂質 0.333 9 55.00
77.50		 $p_{a3'上}=$ 18.32
$p_{a3'下}=$ 25.81
4'層 $ℓ_0$ 砂質 0.333 9 77.50
9$ℓ_0$+77.50		 $p_{a4'上}=$ 25.81
$p_{a4'下}=$ 下式
$$ \begin{equation} \begin{split} p_{a4'下} &=K_a\ (\sum\gamma\ h+q)-2c\sqrt{K_a} \\[5px] &=0.333 \cdot (9 \cdot ℓ_0 + 77.50) - 2 \cdot 0 \sqrt{0.333} \\[5px] &=3.00 \cdot ℓ_0 + 25.81 \end{split}\nonumber \end{equation} $$

ここで、砂質地盤であるため、粘着力$c=0$とする。

また、3’層の厚さ2.5mは、下記のとおり計算している。

$$ \begin{equation} \begin{split} 3'層の厚さ &= 掘削底面まで深さ - 1層の厚さ　- 2層の厚さ \\[5px] &= 5.0 - 1.0 - 1.5 \\[5px] &= 2.5 \ \mathrm{m} \end{split}\nonumber \end{equation} $$

なお、4’層は、3層と4層にまたがる厚さであると想定している。ただし、3層と4層の地盤物性値が同じであるため、4’層は１つの層として扱う。

(2) 受働土圧

受働土圧は次の式で求めます。（H11道仮p.35）

$$ \begin{align} p_p & =K_p \sum\gamma\ h'+2c\sqrt{K_p} \nonumber \\[5px] K_p & =\tan^2\left(45^\circ \ + \ \frac{\phi}{2}\right) \nonumber \end{align} $$

ここに、

  • $p_p$：受働土圧（kN/m²）
  • $K_p$：受働土圧係数
  • $\sum \gamma\ h’$：着目点における地盤の有効土かぶり圧（kN/m²）
  • $\gamma$：各層の土の湿潤単位体積重量（kN/m³）
    • ただし、地下水位以下では水中単位体積重量 $\gamma\ ^\prime$ とする。
  • $h’$：着目点までの各層の層厚（m）
  • $q$：地表面までの上載荷重（kN/m²）
  • $c$：土の粘着力（kN/m²）
  • $\phi$：土のせん断抵抗角（度）

以上をもとに、根入れ部の受働土圧を表計算すると次のとおり。

層厚
$h'$
(m)		 土質 受働土圧係数
$K_p$
$\gamma$
(kN/m³)
$\sum \gamma \ h'$
(kN/m²)		 受働土圧
$p_p$
(kN/m²)
4'層 $ℓ_0$ 砂質 3.00 9 0.00
 $p_{p4'上}=$ 0.00
$p_{p4'下}=$ 下式
$$ \begin{equation} \begin{split} p_{p4'下} &=K_p \cdot \gamma \cdot h' \\[5px] &=3.00 \cdot 9 \cdot ℓ_0 \\[5px] &=27.00 \cdot ℓ_0 \end{split}\nonumber \end{equation} $$
(3) 水圧

水圧は静水圧とし、掘削底面までは深さに比例し増加させ、掘削底面から下はつり合い深さで「0」となるよう減少させる。よって、三角形分布となる。（H11道仮p.38）

層厚
$h$
(m)		 地下水

(m)		 水圧
$p_w$
(kN/m²)
1層 1.00 － $p_{w1上}=0.00$
$p_{w1下}=0.00$
2層 1.50 － $p_{w2上}=0.00$
$p_{w2下}=0.00$
3'層 2.50 2.50 $p_{w3'上}=0.00$
$p_{w3'下}=25.00$
4'層 $ℓ_0$ $ℓ_0$ $p_{w4'上}=25.00$
$p_{w4'下}=0.00$
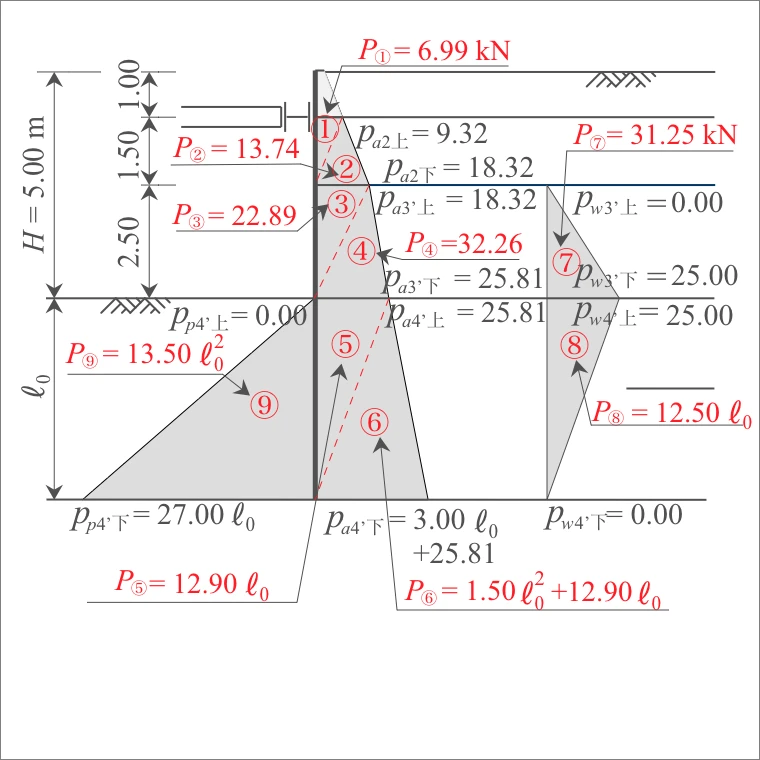
(4) 切ばり位置からのモーメントのつり合い深さ

つり合い深さを算出するには、まず、切ばり位置での「主働側圧による作用モーメント」と、「受働側圧による抵抗モーメント」をそれぞれ求める。そして、それらが等しくなる条件の根入れ長が、つり合い深さとなる。（H11道仮p.87）

まず、側圧を求める。各層を２つに分割した各三角形の面積が側圧となるので、表計算すると下記のとおり。

計算式
底辺×高さ/2
 側圧
$P$
(kN)
2層 ①
②		 9.32 × 1.50 /2
18.32 × 1.50 /2		 6.99
13.74
3'層 ③
④		 18.32 × 2.50 /2
25.81 × 2.50 /2		 22.89
32.26
4'層 ⑤
⑥		 25.81 × ℓ₀/2
(3.00ℓ₀ + 25.81) × ℓ₀/2		 12.90 ℓ₀
1.50 ℓ₀²+12.90 ℓ₀
水 ⑦
⑧		 25.00 × 2.50/2
25.00 × ℓ₀/2		 31.25
12.50 ℓ₀
4'層 ⑨ 27.00ℓ₀ × ℓ₀/2 13.50ℓ₀²

次に、アーム長を求める。

アーム長は、切ばり位置から各三角形の重心までの距離となる。

計算式
（切ばり位置から三角形
重心までの鉛直距離）		 アーム長
$y$
(m)
①
②		 1.50/3×1
1.50/3×2		 0.50
1.00
③
④		 1.50+2.50/3×1
1.50+2.50/3×2		 2.33
3.17
⑤
⑥		 1.50+2.50+ℓ₀/3×1
1.50+2.50+ℓ₀/3×2		 0.33ℓ₀+4.00
0.67ℓ₀+4.00
⑦
⑧		 1.50+2.50/3×2
1.50+2.50+ℓ₀/3×1		 3.17
0.33ℓ₀+4.00
⑨ 1.50+2.50+ℓ₀/3×2 0.67ℓ₀+4.00

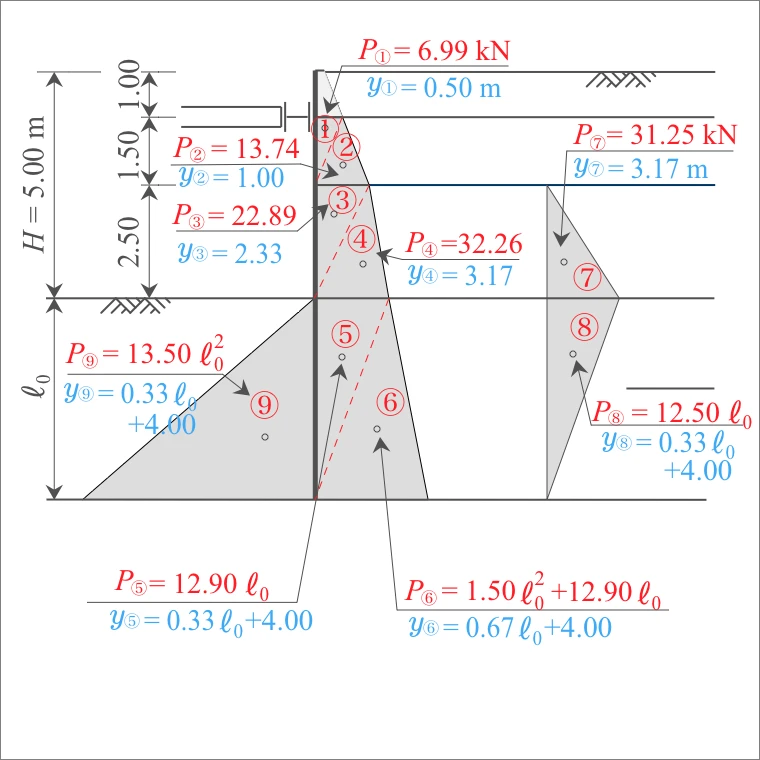
主働土圧による作用モーメント$M_a$は、「側圧 $P_a$」に「アーム長$y$」を乗じて算出する。

$$ M_a = P_a \cdot y $$

表計算すると下記のとおり。

主働側の側圧
$P_a$
(kN)		 アーム長
$y$
(m)		 作用モーメント
$M_a$
(kN・m)
2層 ① 6.99 0.50 3.50
② 13.74 1.00 13.74
3’層 ③ 22.89 2.33 53.42
④ 32.26 3.17 102.15
4’層 ⑤ 12.90ℓ₀ 0.33ℓ₀+4.00 4.30ℓ₀²+51.62ℓ₀
⑥ 1.50ℓ₀²+12.90ℓ₀ 0.67ℓ₀+4.00 1.00ℓ₀³+14.60ℓ₀²+51.62ℓ₀
水 ⑦ 31.25 3.17 98.96
⑧ 12.50 ℓ₀ 0.33ℓ₀+4.00 4.17ℓ₀²+50.00ℓ₀
$\sum M_a=$ 1.00ℓ₀³+23.06ℓ₀²+153.23ℓ₀+271.76

以上より、主働土圧による作用モーメントは下式のとおりとなる。

$$ \begin{equation} \begin{split} \sum M_a = 1.00 {ℓ_0}^3 + 23.06 {ℓ_0}^2 + 153.23 ℓ_0 + 271.76 \end{split}\nonumber \end{equation} $$

今度は、受働土圧による抵抗モーメント$M_p$も同様に算出する。

受働側の側圧
$P_p$
(kN)		 アーム長
$y$
(m)		 作用モーメント
$M_p$
(kN・m)
4’層 ⑨ 13.50ℓ₀² 0.67ℓ₀+4.00 9.00ℓ₀³+54.00ℓ₀²
$\sum M_p=$ 9.00ℓ₀³+54.00ℓ₀²

以上より、受働土圧による抵抗モーメントは下式のとおりとなる。

$$ \sum M_p = 9.00 {ℓ_0}^3 + 54.00 {ℓ_0}^2 $$

つり合い深さは、「主働土圧による作用モーメント」と「受働土圧による抵抗モーメント」が等しい条件の根入れ長なので、下式のとおりとなる。

$$ \sum M_a = \sum M_p $$

変形すると、

$$ \sum M_a - \sum M_p =0 $$

よって、

$$ 1.00 {ℓ_0}^3 + 23.06 {ℓ_0}^2 + 153.23 ℓ_0 + 271.76 -(9.00 {ℓ_0}^3 + 54.00 {ℓ_0}^2)=0 $$
$$ -8.00 {ℓ_0}^3 -30.94 {ℓ_0}^2 + 153.23ℓ_0 + 271.76 =0 $$

カルダノ（Cardano）の公式により、３次方程式の解を求めると、モーメントのつり合い深さは、下記のとおりとなる。

$$ ℓ_0=3.72（掘削底面より下方向に3.72\, \mathrm{m}の位置） $$
📌NOTE
  • カルダノ（Cardano）の公式については、Webを検索すると解説が簡単に見つかりますので、解説はそちらに譲ります。
(5) 根入れ長

根入れ長は、つり合い深さの1.2倍とする。（H11道仮p.87）

よって、根入れ長は、

$$ ℓ=3.72 \times 1.2 = 4.47\ \mathrm{m} $$

なお、参考までに、矢板長の確認のため、地表面から根入れ下部までの距離を計算する。地表面からの距離は、「掘削深さ＋ℓ」なので、

$$ L=5.00 + 4.47 = 9.47\ \mathrm{m} $$

2-1-2. 掘削完了時

(1) 主働土圧

掘削完了時の各層の主働土圧を表計算すると次のとおり。

なお、3層は最下段切ばりの位置で3-1層、3-2層に分割する。

層厚
$h$
(m)		 土質 主働土圧係数
$K_a$
$\gamma$
(kN/m³)
$\sum \gamma \ h+q$
(kN/m²)		 主働土圧
$p_a$
(kN/m²)
1層 1.00 砂質 0.333 18 10.00
28.00		 $p_{a1上}=$ 3.33
$p_{a1下}=$ 9.32
2層 1.50 砂質 0.333 18 28.00
55.00		 $p_{a2上}=$ 9.32
$p_{a2下}=$ 18.32
3-1層 1.50 砂質 0.333 9 55.00
68.50		 $p_{a3-1上}=$ 18.32
$p_{a3-1下}=$ 22.81
3-2層 3.00 砂質 0.333 9 68.50
95.50		 $p_{a3-2上}=$ 22.81
$p_{a3-2下}=$ 31.80
4層 3.00 砂質 0.333 9 95.50
122.50		 $p_{a4上}=$ 31.80
$p_{a4下}=$ 40.79
5層 $ℓ_0$ 砂質 0.271 9 122.50
9$ℓ_0$+122.50		 $p_{a5上}=$ 33.20
$p_{a5下}=$ 下式
$$ \begin{equation} \begin{split} p_{a5下} &=K_a\ (\sum\gamma\ h+q)-2c\sqrt{K_a} \\[5px] &=0.271 \cdot (9 \cdot ℓ_0 + 122.50) - 2 \cdot 0 \sqrt{0.271} \\[5px] &=2.44 \cdot ℓ_0 + 33.20 \end{split}\nonumber \end{equation} $$
(2) 受働土圧

根入れ部の受働土圧を表計算すると次のとおり。

層厚
$h'$
(m)		 土質 受働土圧係数
$K_p$
$\gamma$
(kN/m³)
$\sum \gamma \ h'$
(kN/m²)		 受働土圧
$p_p$
(kN/m²)
4層 3.00 砂質 3.00 9 0.00
 $p_{p4上}=$ 0.00
$p_{p4下}=$ 81.00
5層 $ℓ_0$ 砂質 3.69 9 0.00
 $p_{p5上}=$ 99.63
$p_{p5下}=$ 下式
$$ \begin{equation} \begin{split} p_{p5下} &=K_p\ (\sum\gamma\ h')+2c\sqrt{K_p} \\[5px] &=3.69 \cdot (9 \cdot ℓ_0 + 27.00) + 2 \cdot 0 \sqrt{3.69} \\[5px] &=33.21 \cdot ℓ_0 + 99.63 \end{split}\nonumber \end{equation} $$
(3) 水圧
層厚
$h$
(m)		 地下水

(m)		 水圧
$p_w$
(kN/m²)
1層 1.00 － $p_{w1上}=0.00$
$p_{w1下}=0.00$
2層 1.50 － $p_{w2上}=0.00$
$p_{w2下}=0.00$
3-1層 1.50 1.50 $p_{w3-1上}=0.00$
$p_{w3-1下}=15.00$
3-2層 3.00 3.00 $p_{w3-2上}=15.00$
$p_{w3-2下}=45.00$
4層 3.00 3.00 $p_{w4上}=45.00$
$p_{w4下}=\displaystyle\frac{45.00 ℓ_0}{(ℓ_0 + 3.00)}$
5層 $ℓ_0$ $ℓ_0$ $p_{w5上}=\displaystyle\frac{45.00 ℓ_0}{(ℓ_0 + 3.00)}$
$p_{w5下}=0.00$
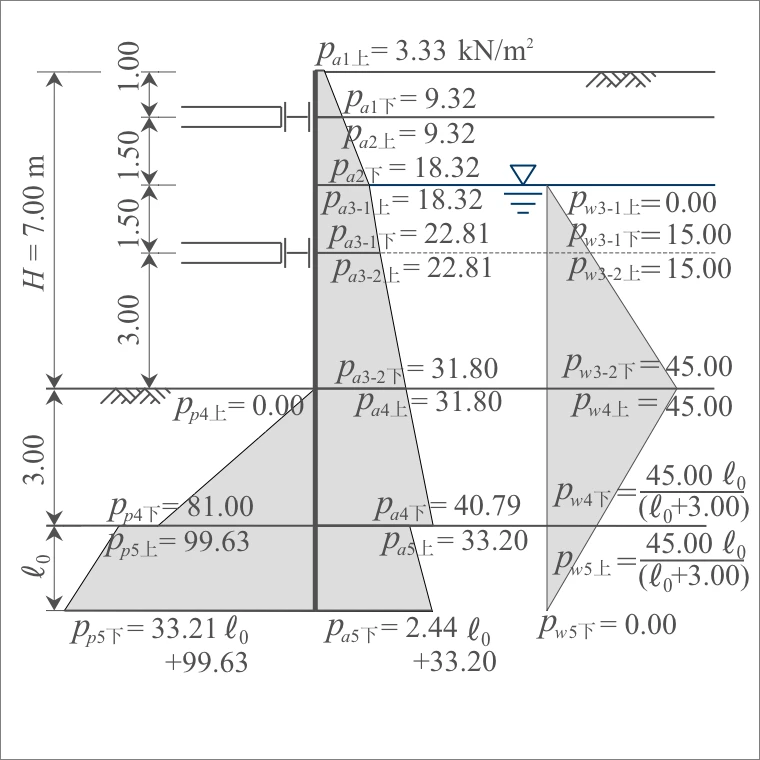
(4) 切ばり位置からのモーメントのつり合い深さ

つり合い深さを算出するには、まず、切ばり位置での「主働土圧による作用モーメント」と、「受働土圧による抵抗モーメント」をそれぞれ求める。そして、それらが等しくなる条件の根入れ長が、つり合い深さとなる。

まず、側圧を求める。各層を２つに分割した各三角形の面積が側圧となるので、表計算すると下記のとおり。

計算式
底辺×高さ/2
 側圧
$P$
(kN)
①
②		 22.81 × 3.00 /2
31.80 × 3.00 /2		 34.22
47.70
③
④		 31.80 × 3.00 /2
40.79 × 3.00 /2		 47.70
61.19
⑤
⑥		 33.20 × ℓ₀/2
(2.44ℓ₀ + 33.20) × ℓ₀/2		 16.60 ℓ₀
1.22ℓ₀²+16.60ℓ₀
⑦
⑧
⑨		 15.00 × 3.00/2
45.00 × 3.00/2
45.00 × (ℓ₀ +3.00)/2		 22.50
67.50
22.50 ℓ₀+67.50
⑩ 81.00 × 3.00 /2 121.50
⑪
⑫		 99.63 × ℓ₀/2
(33.21ℓ₀ + 99.6) × ℓ₀/2		 49.82 ℓ₀
16.61ℓ₀²+49.82ℓ₀

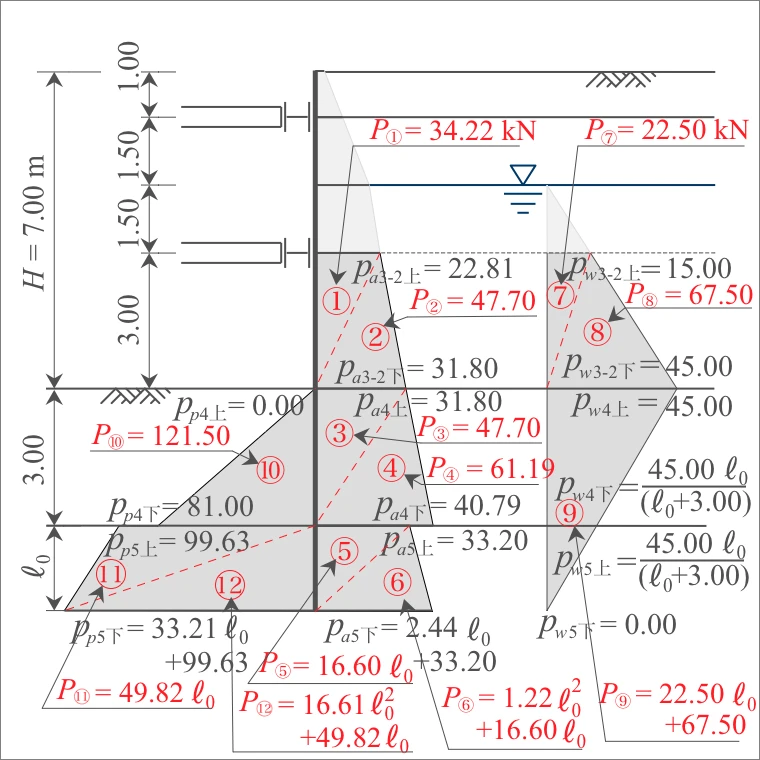
次に、アーム長を求める。

アーム長は、切ばり位置から各三角形の重心までの距離となる。

計算式
（切ばり位置から三角形
重心までの鉛直距離）		 アーム長
$y$
(m)
①
②		 3.00/3×1
3.00/3×2		 1.00
2.00
③
④		 3.00+3.00/3×1
3.00+3.00/3×2		 4.00
5.00
⑤
⑥		 3.00+3.00+ℓ₀/3×1
3.00+3.00+ℓ₀/3×2		 0.33ℓ₀+6.00
0.67ℓ₀+6.00
⑦
⑧
⑨		 3.00/3×1
3.00/3×2
3.00+(3.00+ℓ₀)/3×1		 1.00
2.00
0.33 ℓ₀+4.00
⑩ 3.00+3.00/3×2 5.00
⑪
⑫		 3.00+3.00+ℓ₀/3×1
3.00+3.00+ℓ₀/3×2		 0.33ℓ₀+6.00
0.67ℓ₀+6.00

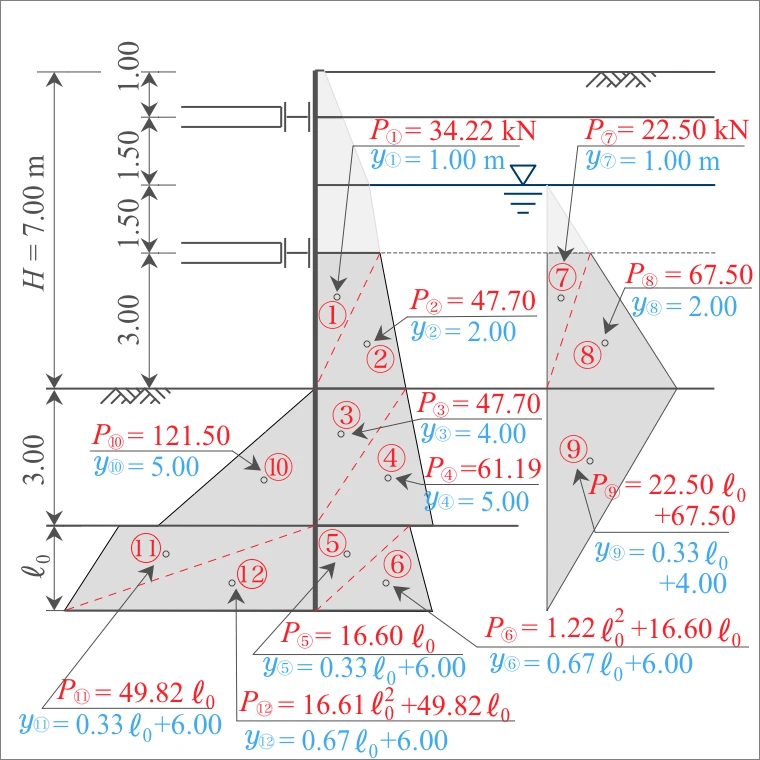
主働土圧による作用モーメント$M_a$は、「側圧$P_a$」に「アーム長$y$」を乗じて算出する。

$$ M_a = P_a \cdot y $$

表計算すると下記のとおり。

主働側の側圧
$P_a$
(kN)		 アーム長
$y$
(m)		 作用モーメント
$M_a$
(kN・m)
3-2層 ① 34.22 1.00 34.22
② 47.70 2.00 95.40
4層 ③ 47.70 4.00 190.81
④ 61.19 5.00 305.94
5層 ⑤ 16.60 ℓ₀ 0.33ℓ₀+6.00 5.53ℓ₀²+99.59ℓ₀
⑥ 1.22ℓ₀²+16.60ℓ₀ 0.67ℓ₀+6.00 0.81ℓ₀³+18.38ℓ₀²+99.59ℓ₀
水 ⑦ 22.50 1.00 22.50
⑦ 67.50 2.00 135.00
⑧ 22.50 ℓ₀+67.50 0.33ℓ₀+4.00 7.50ℓ₀²+112.50ℓ₀+270.00
$\sum M_a=$ 0.81ℓ₀³+31.42ℓ₀²+311.69ℓ₀+1,053.87

以上より、主働土圧による作用モーメントは下式のとおりとなる。

$$ \begin{equation} \begin{split} \sum M_a = 0.81 {ℓ_0}^3 + 31.42 {ℓ_0}^2 +311.69 ℓ_0 + 1,053.87 \end{split}\nonumber \end{equation} $$

今度は、受働土圧による抵抗モーメント$M_p$も同様に算出する。

受働側の側圧
$P_p$
(kN)		 アーム長
$y$
(m)		 作用モーメント
$M_p$
(kN・m)
4層 ⑩ 121.50 5.00 607.50
5層 ⑪ 49.82ℓ₀ 0.33ℓ₀+6.00 16.61ℓ₀²+298.89ℓ₀
　　 ⑫ 16.61ℓ₀²+49.82ℓ₀ 0.67ℓ₀+6.00 11.07ℓ₀³+132.84ℓ₀²+298.89ℓ₀
$\sum M_p=$ 11.07ℓ₀³+149.45ℓ₀²+597.78ℓ₀+607.50

以上より、受働土圧による抵抗モーメントは下式のとおりとなる。

$$ \begin{equation} \begin{split} \sum M_p = 11.07 {ℓ_0}^3 + 149.45 {ℓ_0}^2 + 597.78{ℓ_0} + 607.50 \end{split}\nonumber \end{equation} $$

つり合い深さは、「主働土圧による作用モーメント」と「受働土圧による抵抗モーメント」が等しい条件の根入れ長なので、下式のとおりとなる。

$$ \sum M_a = \sum M_p $$

変形すると、

$$ \sum M_a - \sum M_p =0 $$

よって、

$$ \begin{equation} \begin{split} 0.81 {ℓ_0}^3 + 31.42 {ℓ_0}^2 +311.69 ℓ_0 + 1,053.87 -(11.07 {ℓ_0}^3 + 149.45 {ℓ_0}^2 + 597.78{ℓ_0} + 607.50)=0 \end{split}\nonumber \end{equation} $$
$$ \begin{equation} \begin{split} -10.26 {ℓ_0}^3 -118.03 {ℓ_0}^2 - 286.10 ℓ_0 + 446.37 =0 \end{split}\nonumber \end{equation} $$

カルダノ（Cardano）の公式により、３次方程式の解を求めると、モーメントのつり合い深さは、下記のとおりとなる。

$$ ℓ_0=1.06（掘削底面より下方向に1.06\,\mathrm{m}の位置） $$
(5) 根入れ長

根入れ長は、つり合い深さの1.2倍とする。（H11道仮p.87）

よって、根入れ長は、

$$ ℓ=(ℓ_0 + 3.00) \times 1.2$ $= (1.06 + 3.00) \times 1.2$ $=4.87\ \mathrm{m} $$

地表面からの距離は、「掘削深さ＋ℓ」なので、

$$ L=7.00 + 4.87 = 11.87\ \mathrm{m} $$

2-1-3. 結果の比較

上記より、「最下段切ばり設置直前」と「掘削完了時」、それぞれの根入れ長および地表面からの距離によって、「根入れ部の土圧および水圧に対する安定から必要となる根入れ長」を決定する。

根入れ長さ 【参考】地表面からの距離
最下段切ばり設置直前 4.47 9.47
掘削完了時 4.87 11.87

以上より、土圧および水圧に対する安定から必要となる根入れ長は、

$$ ℓ=4.87\ \mathrm{m} $$

2-2. 土留め壁の許容鉛直支持力から定まる根入れ長

路面覆工などからの鉛直荷重が作用しないので、検討を省略する。（H11道仮p29）

2-3. 掘削底面の安定から定まる根入れ長

掘削底面の安定に必要な根入れ長は、地盤によって異なります。

砂質地盤は「ボイリングおよびパイピングの検討」をすることになります。（H11道仮p.76～82）

2-3-1. ボイリングの検討

(1) 安全率

ボイリングに対する安全率$F_s$を満足するように根入れ長 を求めます。（H11道仮p.79, 29）

$$ F_s = \frac{w}{u} \nonumber $$

ここに、

  • $F_s$：ボイリングに対する安全率　$F_s \geqq 1.2$
  • $w$：土の有効重量（kN/m²）
  • $u$：土留め壁先端位置に作用する平均過剰間隙水圧（kN/m²）
(2) 土の有効重量

土の有効重量$w$は、次のとおり求めます。

$$ w= \gamma \ ^\prime \cdot ℓ_d \nonumber $$

ここに

  • $\gamma \ ^\prime$：土の水中単位体積重量（kN/m³）
  • $ℓ_d$：土留め壁の根入れ長（m）

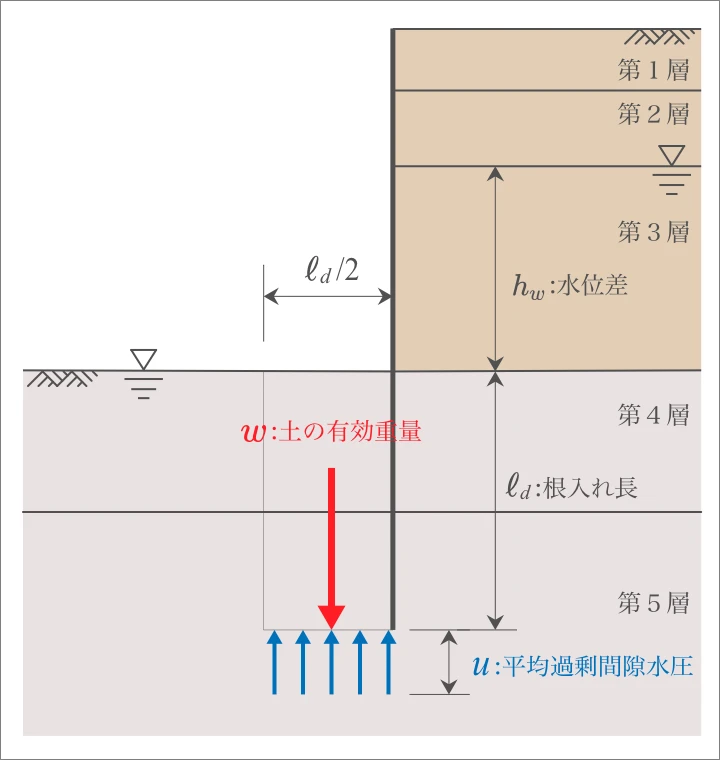
上図のとおり、$w$は4層と5層の有効重量を合計した値となります。このため$\gamma \ ^\prime$は、「掘削底面から根入れ下端までの範囲」における水中単位体積重量の平均値$\bar{\gamma \ ^\prime}$としなければなりません。

📌NOTE
  • $\bar{\gamma \ ^\prime}$を算出するためには、根入れ長$ℓ_d$が必要になってしまいます。
  • しかし、根入れ長$ℓ_d$はこの段階では決まっていません。
  • そこで、「$ℓ_d$の仮定値」を設定し$\bar{\gamma \ ^\prime}$を求め、後述のとおり 「$ℓ_d$の計算値」を算出します。この後、仮定値と計算値の差が「0」に収れんするまで、仮定値を見直して繰り返し計算（Excelのゴールシーク）して$ℓ_d$を決定します。

繰り返し計算した結果が下記の表です。

層厚
$h$
(m)		 単位体積重量
$\gamma$
(kN/m³)		 ボイリング検討用の
水中単位重量算出
のため差し引く値		 水中単位重量
$\gamma \ ^\prime$
(kN/m³)
$h \cdot \gamma \ ^\prime$
(kN/m²)
4層 3.00 18 -10.0 8.0 24.0
5層 1.73 18 -10.0 8.0 13.8
$\sum$ 4.73 37.8

根入れ長$ℓ_d$が「4.73」と計算されました。

よって、水中単位体積重量の平均値$\bar{\gamma \ ^\prime}$は

$$ \begin{equation} \begin{split} \bar{\gamma \ ^\prime} &=\frac{\sum ( h \cdot \gamma \ ^\prime )}{\sum h} \ =\frac{37.8}{4.73} \ =8.0\ \mathrm{kN/m^3} \end{split}\nonumber \end{equation} $$

となる。

(3) 土留め壁先端位置に作用する平均過剰間隙水圧

土留め壁先端位置に作用する平均過剰間隙水圧$u$は、次のとおり求めます。

$$ u=\lambda\ \frac{1.57 \cdot \gamma_w \cdot h_w}{4} \nonumber $$

ここに、

  • $\gamma_w$：水の単位体積重量（kN/m³） $\gamma_w=10.0\,\mathrm{kN/m^3}$
  • $h_w$：水位差（m）$h_w =4.5\,\mathrm{m}$
  • $\lambda$：土留めの形状に関する補正係数
    • $\lambda = \lambda_1 \cdot \lambda_2$
      • $\lambda_1$：掘削幅に関する補正係数
      • $\lambda_1 = 1.30 +$ $0.7 \ (B_e/ℓ_d)^{-0.45}$
        • $B_e$：掘削幅（m）　$B_e=7.2\,\mathrm{m}$
        • ただし、$\lambda_1< 1.5$ のときは、$\lambda_1=1.5$ とする。
        • （前述のとおり の算出は、繰り返し計算（Excelならばゴールシーク）により求めます。）
      • よって、
      • $\lambda_1=1.30+$ $0.7\ (7.2/4.73)^{-0.45}$ $=1.88$
      • 以上より、
      • $\lambda_1=1.88$
      • $\lambda_2$：土留め平面形状に関する補正係数
      • $\lambda_2=0.95+0.09$ ${(L_e/B_e)+0.37}^{-2}$
        • $L_e$：掘削長さ（m）　$L_e=36.0\ \mathrm{m}$
      • よって、
      • $\lambda_2= 0.95+0.09 \times$ $(36.0/7.2)+$ $0.37^{-2}=0.95$
(4) ボイリングに対して安全な根入れ長

安全率は

$$ \begin{equation} F_s=\frac{w}{u} = \frac{\bar{\gamma \ ^\prime} \cdot ℓ_d \cdot 4}{\lambda_1 \cdot \lambda_2 \cdot 1.57 \cdot \gamma_w \cdot h_w}\nonumber \end{equation} $$

であるため、式を変形し、ボイリングに対して安全率を満足する「$ℓ_d$の計算値」を求めます。

$$ \begin{equation} \begin{split} ℓ_d &=\frac{F_s \cdot \lambda_1 \cdot \lambda_2 \cdot 1.57 \cdot \gamma_w \cdot h_w}{\bar{\gamma \ ^\prime} \cdot 4} \\[5px] &=\frac{1.2 \cdot 1.88 \cdot 0.95 \cdot 1.57 \cdot 10.0 \cdot 4.5}{8.0\cdot 4}\\[5px] &=4.73\ \mathrm{m} \end{split}\nonumber \end{equation} $$
📌NOTE
  • ボイリングの検討において注意すべき点は、土の水中単位体積重量を計算するために差し引く値が「10.0kN/m³」となっていることです。（H11道仮）
  • 一方、先の「2-1. 根入れ部の土圧および水圧に対する安定から必要となる根入れ長」の主働土圧を計算した際の差し引く値は「9.0kN/m³」です。

2-3-2. パイピングの検討

浸透流路長と水位差の比を考慮した式を用いる。（H11道仮p.82）

$$ ℓ_h + ℓ_d \geqq 2 \cdot h_w　\nonumber $$

ここに、

  • $ℓ_h$：背面側の浸透流路長（m）
  • ただし、背面地盤に礫層のような透水性の大きな地層がある場合はその層圧を$ℓ_d$から控除する。

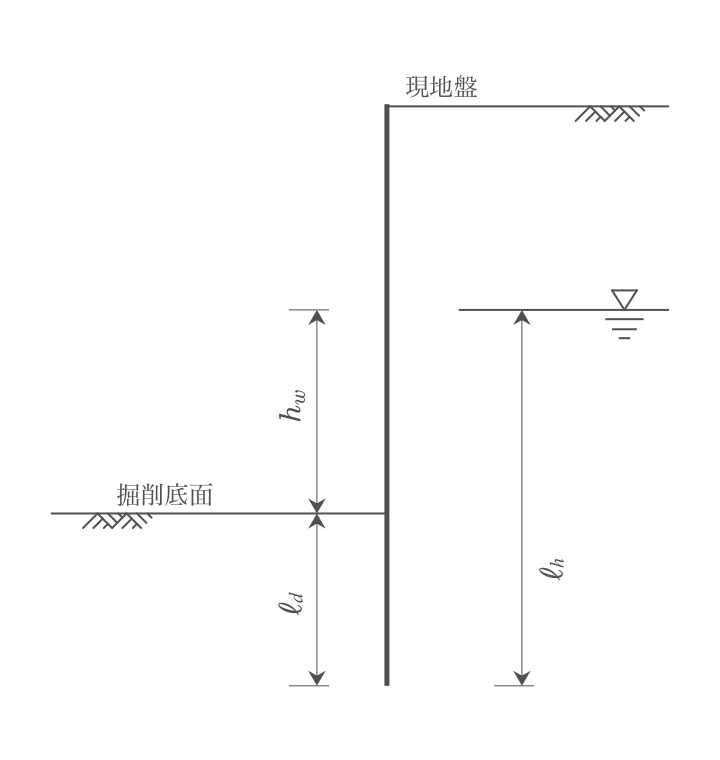
陸上であるため、

$$ (ℓ_d + h_w) + ℓ_d \geqq 2 \cdot h_w \nonumber $$

変形すると、

$$ ℓ_d \geqq h_w/2 = 4.5/2 = 2.25 \ \mathrm{m} \nonumber $$

2-3-3. 結果の比較

上記より、「ボイリングの検討」による根入れ長と、「パイピングの検討」による根入れ長を比較し、長い方を「掘削底面の安定から定まる根入れ長」とする。

根入れ長さ
ボイリングの検討 4.73
パイピングの検討 2.25

以上より、掘削底面の安定から定まる根入れ長は、

$$ ℓ_d=4.73\ \mathrm{m} $$

2-4. 最小根入れ長

鋼矢板なので、最小の根入れ長は「3.0m」とします。（H11道仮p.87）

$$ ℓ_{min}=3.0\ \mathrm{m} \nonumber $$

2-5 根入れ長の決定

根入れ長は、それぞれの計算により求められる根入れ長のうち最も長いものとする。（H11道仮p.87）

計算方法 計算結果
土圧および水圧に対する安定から必要となる根入れ長 $ℓ_0=4.87$
掘削底面の安定から決定される根入れ長 $ℓ_d=4.73$
最小根入れ長 $ℓ_{min}=3.00$

よって、根入れ長$D=4.87\ \mathrm{m}$

2-6 鋼矢板の長さ

鋼矢板の長さは、「掘削深さ」に「根入れ長」を加え、0.5m単位で切り上げる。

$$ \begin{equation} \begin{split} L &= H+D\\[5px] &= 7.0+4.87\\[5px] &= 11.87\\[5px] &\fallingdotseq 12.0\ \mathrm{m} \end{split} \nonumber \end{equation} $$

ただし、リース材の標準保有長さ（H11道仮p.321）の範囲外、最小長さ未満の場合は、鋼矢板の型式を見直すこと。（保有長さは地域により異なる。）

型式$\mathrm{I}\hspace{-1.6pt}\mathrm{I}\hspace{-1.6pt}\mathrm{I}$型については、

  • 標準保有長さ　6.0～15.0m
  • 最小長さ　5.0m

であるため、L=12.0mはOK。

3. 壁体の断面力算定

土留め壁の断面計算に用いる最大曲げモーメントは、「掘削完了時における最下段切ばり」、「最下段切ばり設置直前における一段上の切ばり」と、それぞれの場合の「仮想支持点」間をスパンとする単純ばりとし、この両方の場合について断面決定用土圧を作用させて計算する。（H11道仮p90）

断面決定用の土圧と水圧は、根入れ長の計算で用いた値を用いる。（H11道仮p91, 35）

3-1. 最下段切ばり設置直前

3-1-1. 仮想支持点の計算

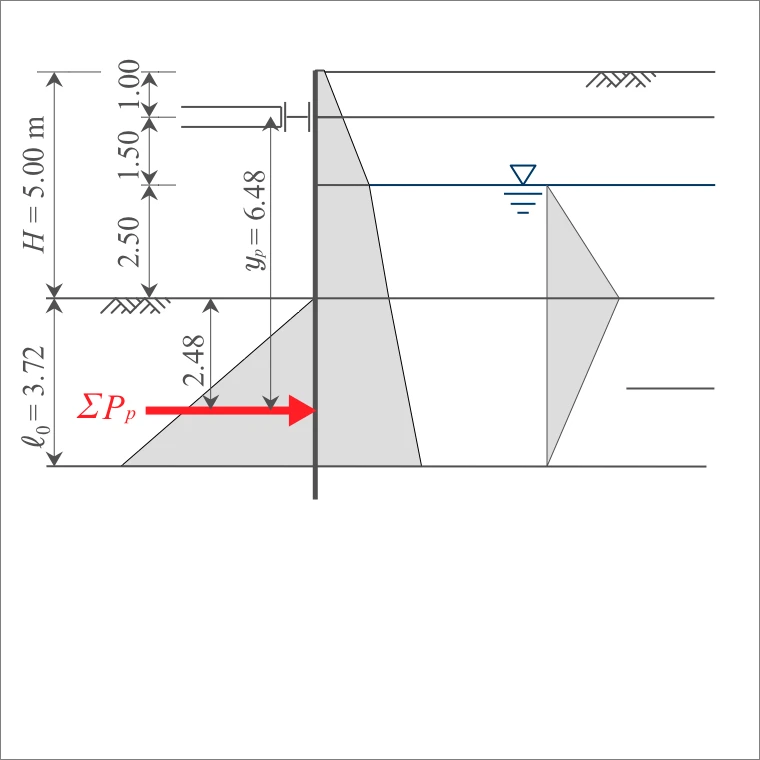
仮想支持点は、土留め壁の根入れ長決定のための安定計算で「つり合い深さ」を求めた際の受働抵抗の合力の作用点とする。（H11道仮p91）

切ばりから、下方向にある仮想支持点までの距離は、下式により算出する。

$$ y_p= \frac{\sum M_p}{\sum P_p}\nonumber $$

ここに、

$$ \sum M_p = 9.00 {ℓ_0}^3 + 54.0 {ℓ_0}^2 $$
$$ \sum P_p = 13.50 {ℓ_0}^2 $$
$$ ℓ_0 =3.72 $$

であるため、

$$ \begin{equation} \begin{split} y_p &=\frac{9.00 \times 3.72^3 + 54.0 \times 3.72^2}{13.50 \times 3.72^2} \\[5px] &=\frac{1,214.0}{187.3} \\[5px] &=6.48\ \mathrm{m} \end{split}\nonumber \end{equation} $$
なお、切ばりから掘削底面までの距離は、4.00mであるため、掘削底面から仮想支持点までの距離は、
$$ 6.48 - 4.00 = 2.48\ \mathrm{m} $$
となる。
📌NOTE
  • 今回の計算例のように受働土圧が１層である場合は、つり合い深さから直接算出することもできる。
  • つまり、受働土圧の三角形分布における重心（受働抵抗の合力の作用点）から掘削底面までの距離を計算すると、3.72 × 2 / 3 = 2.48mとなる。

3-1-2. 最大曲げモーメントの計算

(1) 切ばり位置における反力

切ばり位置をA点、仮想支持点をB点とする単純ばりを仮定し、A点における反力を計算する。（H11道仮p.91）

a. 土圧

まず、単純ばりに作用させる断面決定用土圧は、H11道仮p36～38に従って算出する。

土の平均単位体積重量は、地表面から仮想支持点までの間における各層の平均なので
$$ \begin{equation} \begin{split} \bar{\gamma} &=\frac{\sum h \cdot \gamma}{\sum h} \\[5px] &=\frac{89.85}{7.48} \\[5px] &=12.01 \ \mathrm{kN/m^3} \end{split}\nonumber \end{equation} $$
層厚
$h$
(m)
$\gamma$
(kN/m³)
$h \cdot \gamma$
(kN/m²)
1層 1.00 18 18.00
2層 1.50 18 27.00
3'層 2.50 9 22.50
4'層 2.48 9 22.35
$\sum$ 7.48 89.85
掘削深さHによる係数は、掘削深さ：5.0mであるため、a=1 地質による係数は、土質：砂質であるため、b=2 よって、主働土圧は、
$$ \begin{equation} \begin{split} p &=a \cdot b \cdot \gamma \\[5px] &=1 \cdot 2 \cdot 12.01 \\[5px] &=24.01 \ \mathrm{kN/m^2} \end{split}\nonumber \end{equation} $$

なお、地表面での上載荷重は、平均単位体積重量を用いて「厚さ」に換算する。

$$ \begin{equation} \begin{split} 換算土圧 &=\frac{q}{\gamma} \\[5px] &=\frac{10.0}{12.01} \\[5px] &=0.83 \ \mathrm{m} \end{split}\nonumber \end{equation} $$
b. 水圧

土留めに作用する水圧は静水圧とし、掘削底面まで増加、掘削底面からつり合い深さまで減少する三角形分布とする。

c. 受働土圧

受働土圧は、根入れ長の決定に用いた値を採用する。

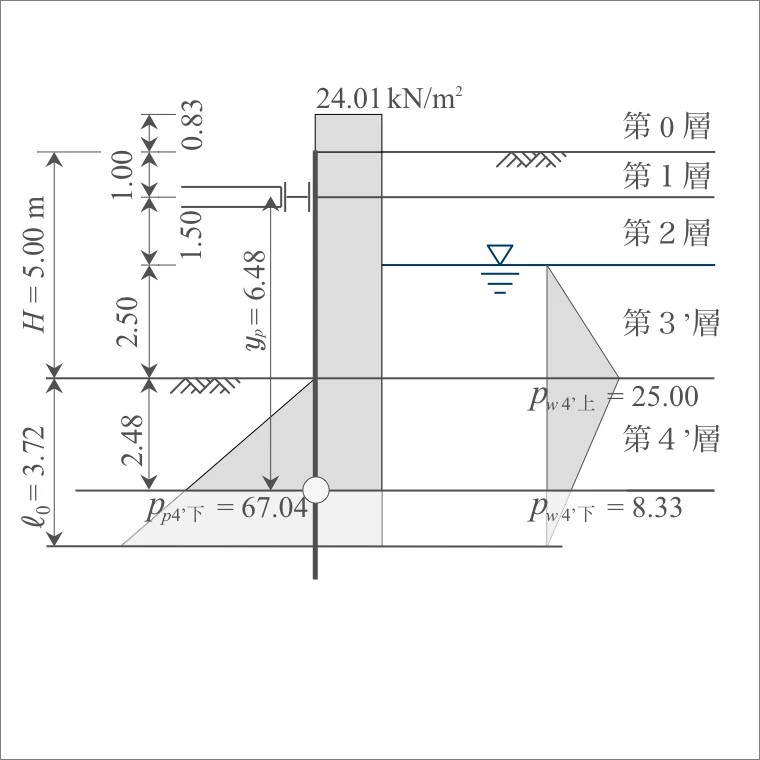
d. A点における反力の計算

まず、各層の主働土圧、水圧、受働土圧を合計する。

層厚
$h$
(m)		 主働土圧
$p_a$
(kN/m²)		 水圧
$p_w$
(kN/m²)		 受働土圧
$p_p$
(kN/m²)		 計
$p=p_a+p_w-p_p$
(kN/m²)
0層 上面
下面		 0.83 $p_{a0上}=24.01$
$p_{a0下}=24.01$		 - - $p_{0上}=24.01$
$p_{0下}=24.01$
1層 上面
下面		 1.00 $p_{a1上}=24.01$
$p_{a1下}=24.01$		 - - $p_{1上}=24.01$
$p_{1下}=24.01$
2層 上面
下面		 1.50 $p_{a2上}=24.01$
$p_{a2下}=24.01$		 - - $p_{2上}=24.01$
$p_{2下}=24.01$
3'層 上面
下面		 2.50 $p_{a3'上}=24.01$
$p_{a3'下}=24.01$		 $p_{w3'上}=0.00$
$p_{w3'下}=25.00$		 - $p_{3'上}=24.01$
$p_{3'下}=49.01$
4'層 上面
下面		 2.48 $p_{a4'上}=24.01$
$p_{a4'下}=24.01$		 $p_{w4'上}=25.00$
$p_{w4'下}=8.33$		 $p_{p4'上}=0.00$
$p_{p4'下}=67.04$		 $p_{4'上}=49.01$
$p_{4'下}=-34.69$
掘削底面からp=0までの距離を$ℓ_e$とすると、
$$ \begin{equation} \begin{split} \frac{p_{4'上}}{p_{4'下}} &=\frac{ℓ_e}{2.48-ℓ_e} \\[5px] \frac{49.01}{34.69} &=\frac{ℓ_e}{2.48-ℓ_e} \\[5px] ℓ_e &=\frac{2.48 \times 49.01}{34.69 + 49.01} \\[5px] ℓ_e &=1.45 \ \mathrm{m} \end{split}\nonumber \end{equation} $$

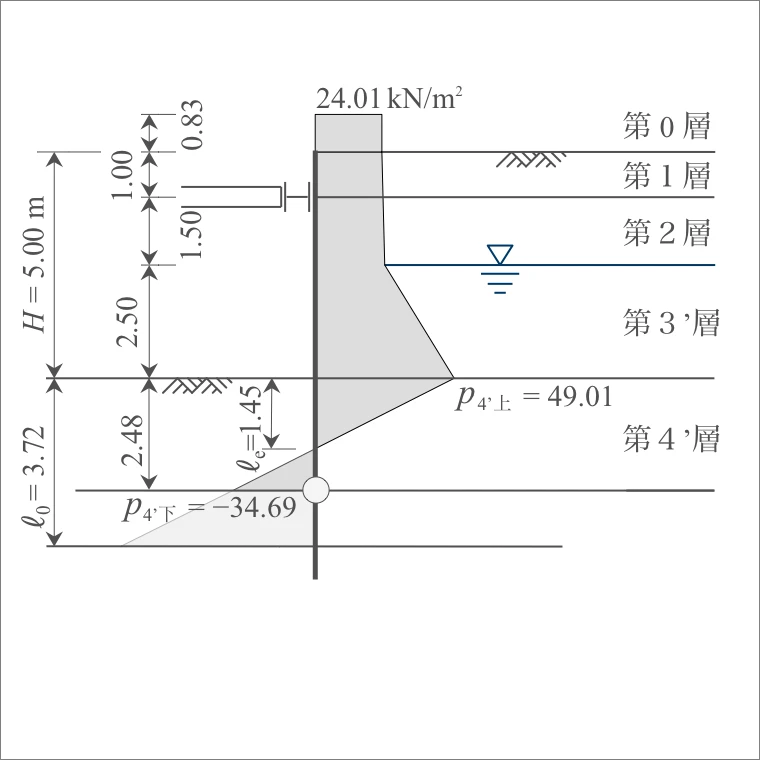
断面力の算定は、切ばりと仮想支持点を支点とする単純ばりとして計算する。

また、pが負となる作用力は無視する。

層厚
$h$
(m)
$p$
(kN/m²)
2層 上面
下面		 1.50 $p_{A}=24.01$
$p_{2下}=24.01$
3'層 上面
下面		 2.50 $p_{3'上}=24.01$
$p_{3'下}=49.01$
4'層 上面
0点		 1.45 $p_{4'上}=49.01$
$p_{0}=0.00$
A点（切ばり位置）から$p=0$の位置までを図のとおり、各層で分割し、その面積「側圧$P$」を求める。
計算式 側圧
$P$
(kN)
① 24.01×(1.50+2.50)= 96.05
② (49.01-24.01)×2.50/2= 31.25
③ 49.01×1.45/2= 35.63
B点（仮想支持点）から各重心までの距離「アーム長$y$」を求める。
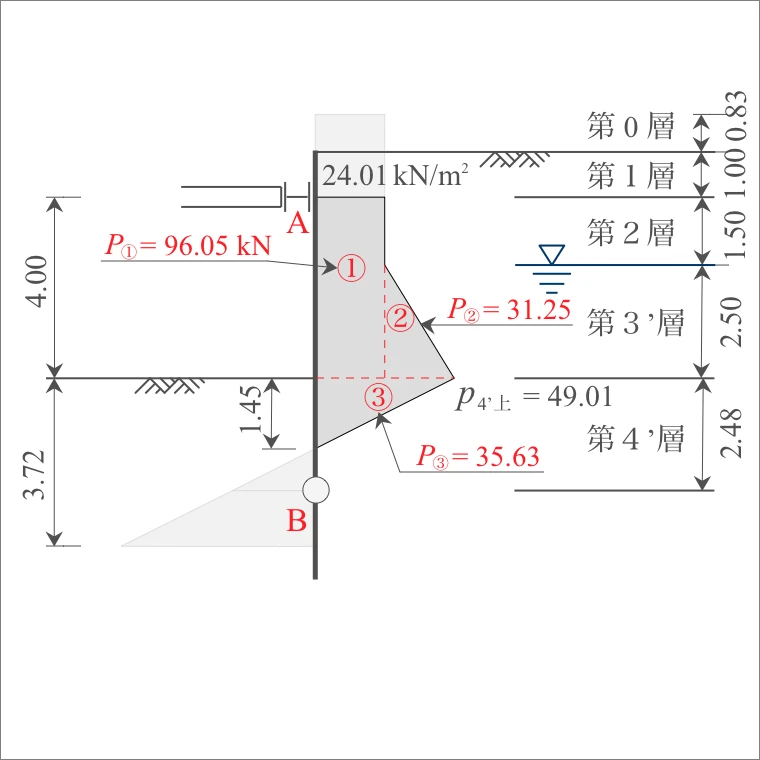
計算式 B点からのアーム長
$y$
(m)
① 2.48+4.00/2= 4.48
② 2.48+2.50/3×1= 3.32
③ (2.48-1.45)+1.45/3×2= 2.00

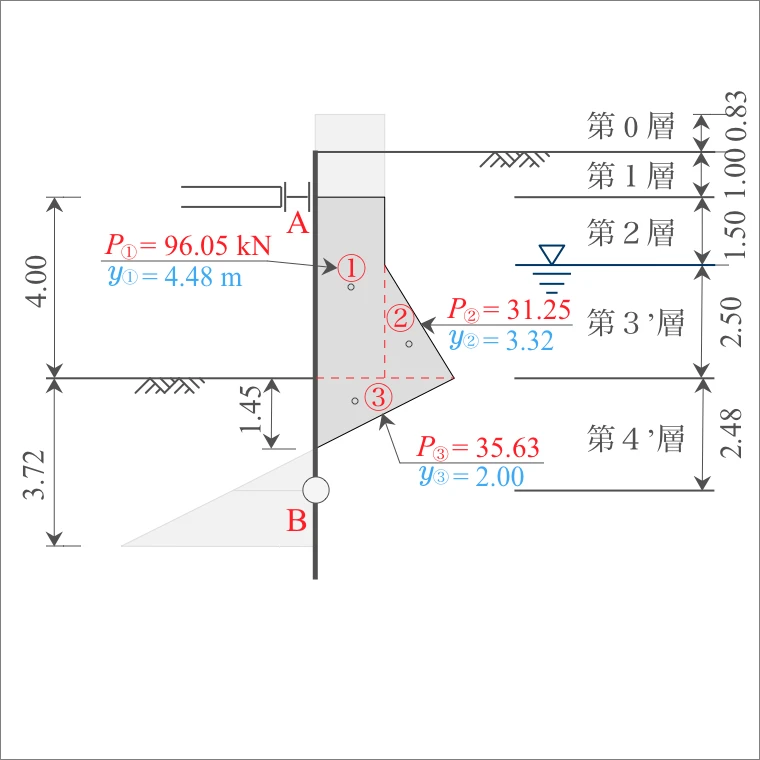
側圧$P$にアーム長$y$を乗じて、B点での作用力によるモーメント$M_B$を算出する。

側圧
$P$
(kN)		 アーム長
$y$
(m)		 モーメント
$M_B$
(kN・m)
① 96.05 4.48 430.61
② 31.25 3.32 103.63
③ 35.63 2.00 71.20
∑ 605.44

よって、A点（切ばり位置）における反力$R_A$は、B点でのモーメントのつり合いより、

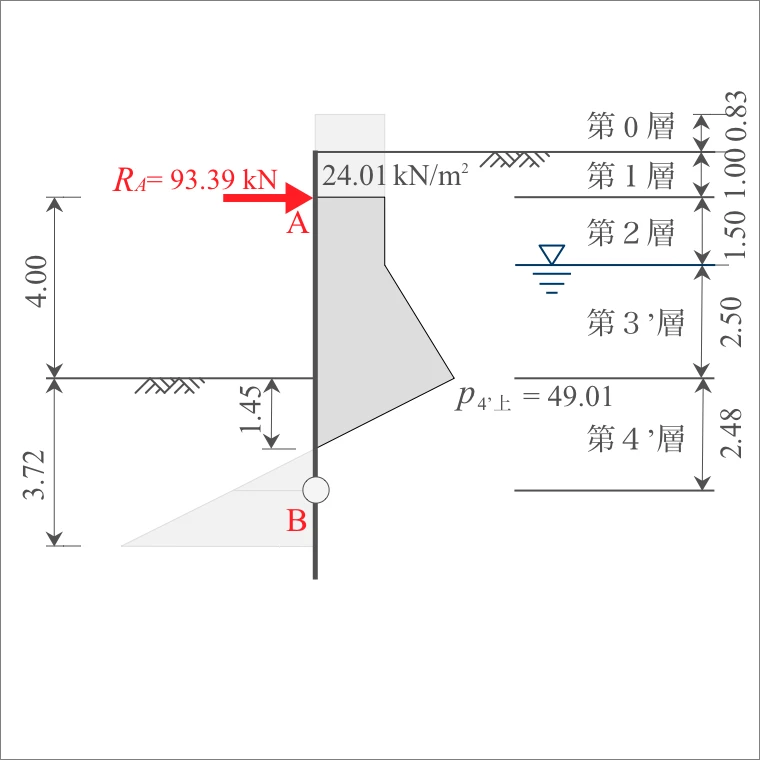
$$ (A点からB点までの距離)\times R_A = \sum M_B $$ $$(2.48 + 4.00)\times R_A=605.44$$ よって、切ばり位置における反力は $$R_A=93.39\ \mathrm{kN}$$
(2) 土圧・水圧による曲げモーメント

最大曲げモーメントは、AB間の中央付近である「３’層」で発生すると想定されるので、３’層の境界から下方向に距離 「$x$」 を定義し、その「$x$」から上部方向における曲げモーメントを計算する。

📌NOTE
  • 最大曲げモーメントの発生位置をある程度想定した方が計算が簡単になります。
  • もし、計算結果が「３'層」に収まらない場合は、別の層で再度計算することになります。
A点（切ばり位置）から$x$の位置までを図のとおり、各層で分割する。
層厚
$h$
(m)		 計
$p$
(kN/m²)
2層 A
下面		 1.50 $p_{2上}=$ 24.01
$p_{2下}=$ 24.01
3'層 上面
$x$		 2.50 $p_{3'上}=$ 24.01
$p_{x}= $ 10 $x$ +24.01
$x$
下面		 $p_{x}=$ 10 $x$ +24.01
$p_{3'下}=$ 49.01

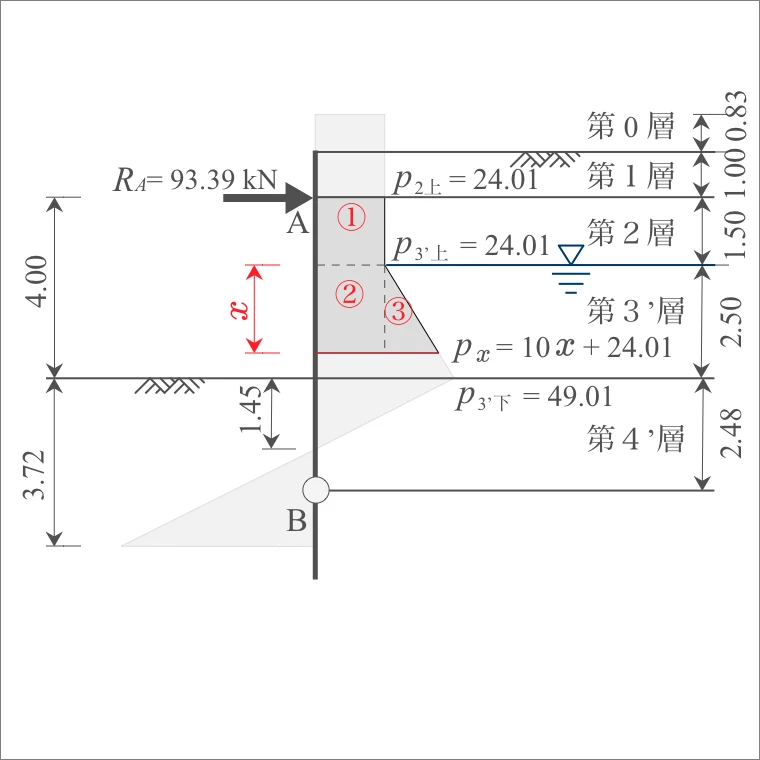
ここで、

$$ \begin{equation} \begin{split} p_x &=\frac{(49.01 - 24.01)}{2.50} x + 24.01\\[5px] &=10 x + 24.01 \end{split}\nonumber \end{equation} $$
分割した箇所のそれそれの面積「側圧$P$」を求める。
計算式 側圧
$P$
(kN)
① 24.01×1.50= 36.02
② 24.01 × $x$ = 24.01 $x$
③ 10 × $x^2$ /2= 5.00 $x^2$
$x$点から各図形の重心までの距離「アーム長$y$」を求める。
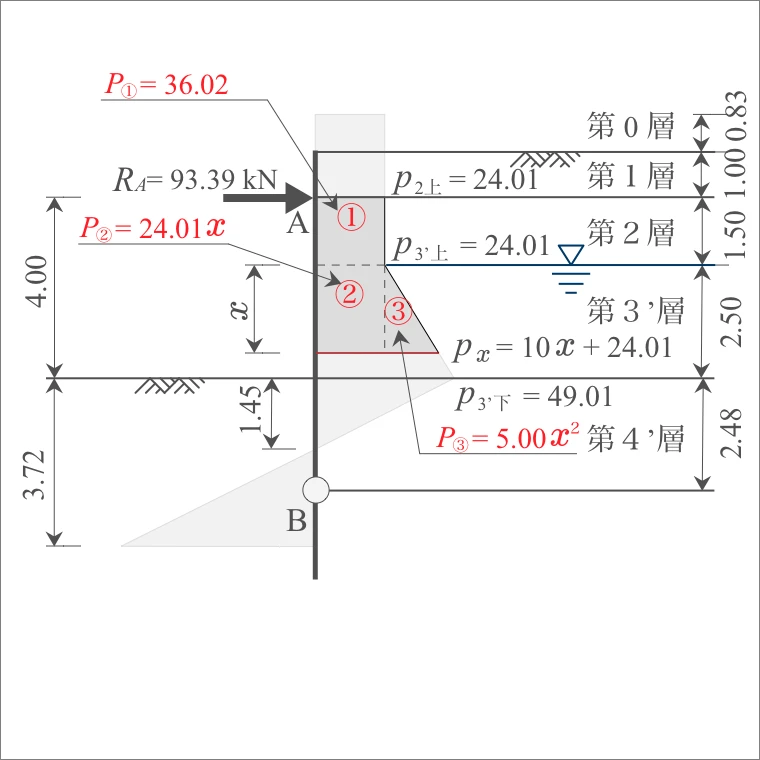
計算式
$x$点から重心の鉛直距離		 アーム長
$y$
(m)
① $x$ +1.50/2= $x$ +0.75
② $x$/2= 0.50 $x$
③ $x$/3×1= 0.33 $x$

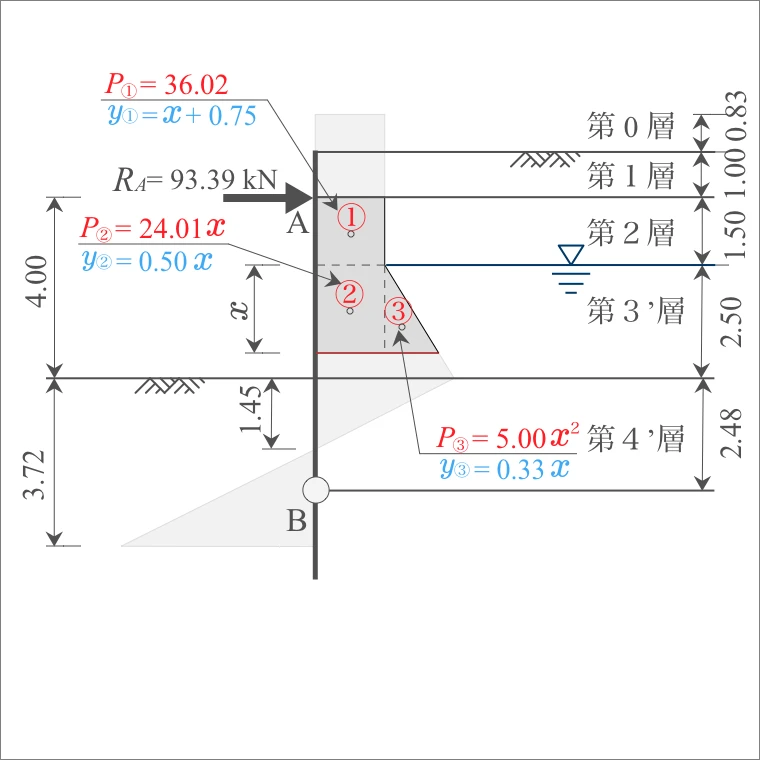
モーメント$M$は、「側圧$P$」に「アーム長$y$」を乗じて算出する。

$$ M = P \cdot y $$

表計算すると下記のとおり。

側圧
$P$
(kN)		 アーム長
$y$
(m)		 作用モーメント
$M$
(kN・m)
2層 ① 36.02 $x$+0.75 36.02 $x$+27.02
3層 ② 24.01 $x$ 0.50 $x$ 12.01 $x^2$
③ 5.00 $x^2$ 0.33 $x$ 1.67 $x^3$
$\sum M=$ 1.67$x^3$+12.01$x^2$+36.02$x$+27.02

以上より、作用モーメントは下式のとおりとなる。

$$ \sum M= 1.67 x^3 +12.01 x^2 +36.02 x +27.02 $$
(3) 最大曲げモーメント

(1),(2)より、任意点ｘでの曲げモーメントは、下式のとおりとなる。

$$ \begin{equation} \begin{split} M_x &=R_A \cdot ( x + 1.50)-(1.67 x^3+ 12.01 x^2+36.02x+27.02) \\[5px] &=93.39 \cdot ( x + 1.50)-(1.67x^3+12.01 x^2+36.02x+27.02) \\[5px] &=-1.67x^3 -12.01x^2+57.37x+113.07 \end{split} \nonumber \end{equation} $$

微分すると、

$$ M_x ^\prime =-5.00x^2 -24.01x+57.37 \nonumber $$

最大曲げモーメントの位置は、上式=0となるため、

$$ \begin{equation} \begin{split} x &=\frac{24.01- \sqrt{24.01^2 - 4 \times -5.00 \times 57.37}}{2 \times -5.00}\\[5px] &=1.75\ \mathrm{m} \end{split} \nonumber \end{equation} $$

よって、最大曲げモーメントの値は、

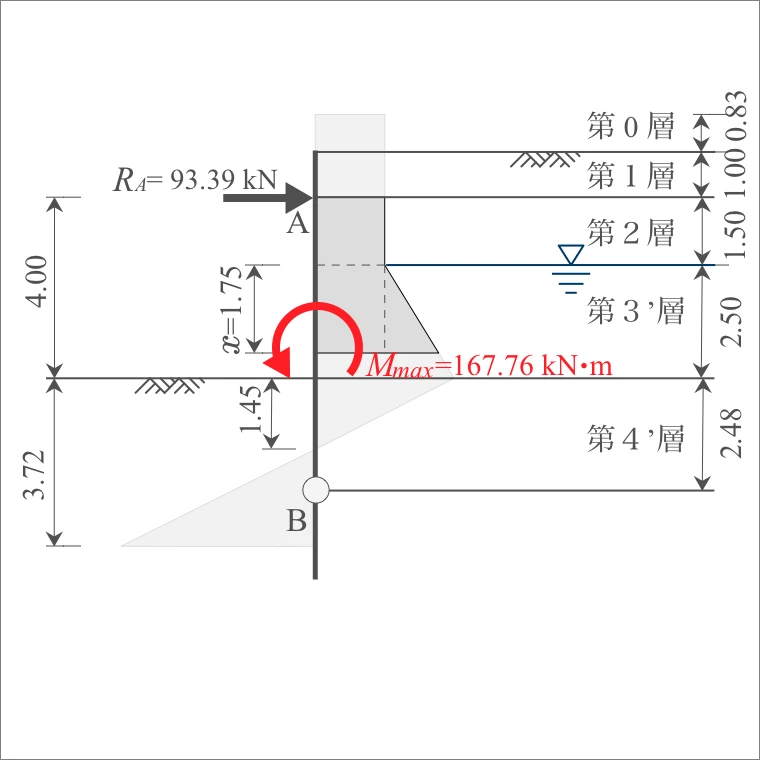
$$ \begin{equation} \begin{split} M_{max} &=-1.67 \times 1.75^3 - 12.01 \times 1.75^2 + 57.37 \times 1.75 + 113.07\\[5px] &=167.76\ \mathrm{kN・m} \end{split} \nonumber \end{equation} $$

3-1-3. 曲げ応力度の照査

鋼矢板に発生する最大曲げ応力度が、許容応力度以下であれば「OK」と判定し、「3-2. 掘削完了時」に進む。
許容応力度をを超えた場合は「NG」と判定し、「1-3. 鋼矢板の設定」に戻り、鋼矢板の型式を上げる。（H11道仮p.109）

$$ \sigma_{max}=\frac{M_{max}}{Z \cdot e} \nonumber $$

ここに、

  • $\sigma_{max}$：鋼矢板に発生する最大曲げ応力度（N/mm²）
  • $Z$：断面係数（m³/m）$Z=1,340.0\ \mathrm{cm^3/m}=0.0013400\ \mathrm{m^3/m}$
  • $e$：断面係数の有効率（応力度の計算）$e=60\%$

よって、

$$ \begin{equation} \begin{split} \sigma_{max} &=\frac{167.76}{0.0013400 \cdot 0.6}\\[5px] &=208,659\ \mathrm{kN/m^2}\\[5px] &=208.7\ \mathrm{N/mm^2} \leqq \sigma_{sa}=270.0\ \mathrm{N/mm^2} \ \mathrm{OK} \end{split}\nonumber \end{equation} $$

3-2. 掘削完了時

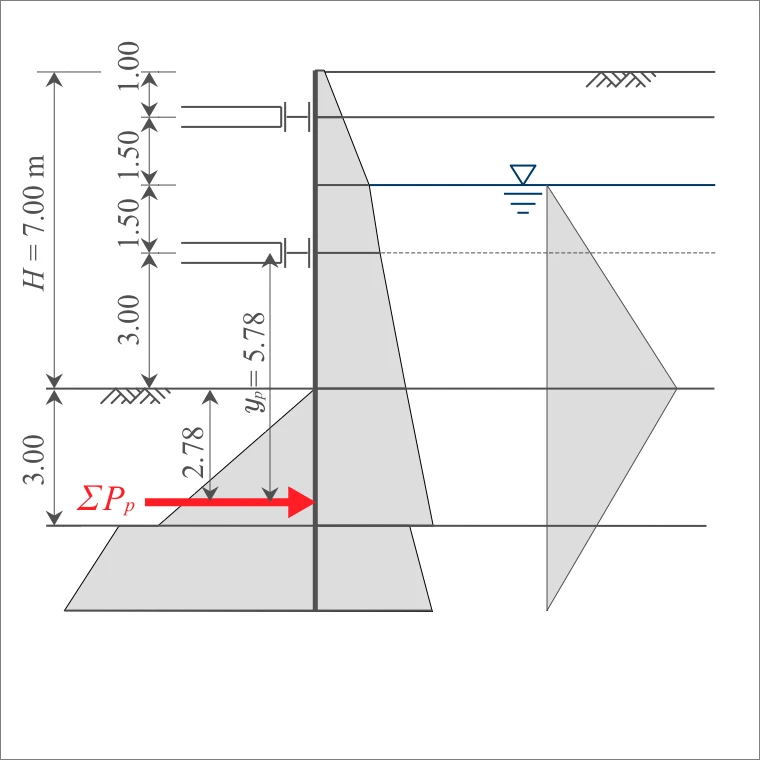
3-2-1. 仮想支持点の計算

仮想支持点は、土留め壁の根入れ長決定のための安定計算で「つり合い深さ」を求めた際の受働抵抗の合力の作用点とする。（H11道仮p91）

最下段切ばりから、下方向にある仮想支持点までの距離は、下式により算出する。

$$ y_p= \frac{\sum M_p}{\sum P_p}\nonumber $$

ここに、

$$ \begin{equation} \begin{split} \sum M_p = 11.07 {ℓ_0}^3 + 149.45 {ℓ_0}^2 + 597.78 ℓ_0 + 607.50 \end{split}\nonumber \end{equation} $$
$$ \begin{equation} \begin{split} \sum P_p = 16.61 {ℓ_0}^2 + 99.63 ℓ_0 + 121.5 \end{split}\nonumber \end{equation} $$
$$ \begin{equation} \begin{split} ℓ_0 =1.06\ \mathrm{m} \end{split}\nonumber \end{equation} $$

であるため、

$$ \begin{equation} \begin{split} y_p &=\frac{11.07 \times 1.06^3 + 149.45 \times 1.06^2 + 597.78 \times 1.06 + 607.50}{16.61 \times 1.06^2 + 99.63 \times 1.06 +121.5} \\[5px] &=\frac{1,419.4}{245.4} \\[5px] &=5.78\ \mathrm{m} \end{split}\nonumber \end{equation} $$
なお、切ばりから掘削底面までの距離は、3.00mであるため、掘削底面から仮想支持点までの距離は、
$$ 5.78 - 3.00 = 2.78\ \mathrm{m} $$
となる。
仮想支持点の最小値は、「掘削底面以深75cm（H11道仮p91）」であるが、2.78 ≧ 0.75なので、掘削底面から仮想支持点までの距離は、
$$ 2.78 \ \mathrm{m} $$
となる。

3-2-2. 最大曲げモーメントの計算

(1) 切ばり位置における反力

切ばり位置をA点、仮想支持点をB点とする単純ばりを仮定し、A点における反力を計算する。（H11道仮p.91）

a. 土圧

まず、単純ばりに作用させる断面決定用土圧は、H11道仮p36～38に従って算出する。

土の平均単位体積重量は、地表面から仮想支持点までの間における各層の平均なので
$$ \begin{equation} \begin{split} \bar{\gamma} &=\frac{\sum h \cdot \gamma}{\sum h} \\[5px] &=\frac{110.56}{9.78} \\[5px] &=11.30 \ \mathrm{kN/m^3} \end{split}\nonumber \end{equation} $$
層厚
$h$
(m)
$\gamma$
(kN/m³)
$h \cdot \gamma$
(kN/m²)
1層 1.00 18 18.00
2層 1.50 18 27.00
3層 4.50 9 40.50
4層 2.78 9 25.06
$\sum$ 9.78 110.56
掘削深さHによる係数は、掘削深さ：7.0mであるため、a=1
地質による係数は、土質：砂質であるため、b=2
よって、主働土圧は、
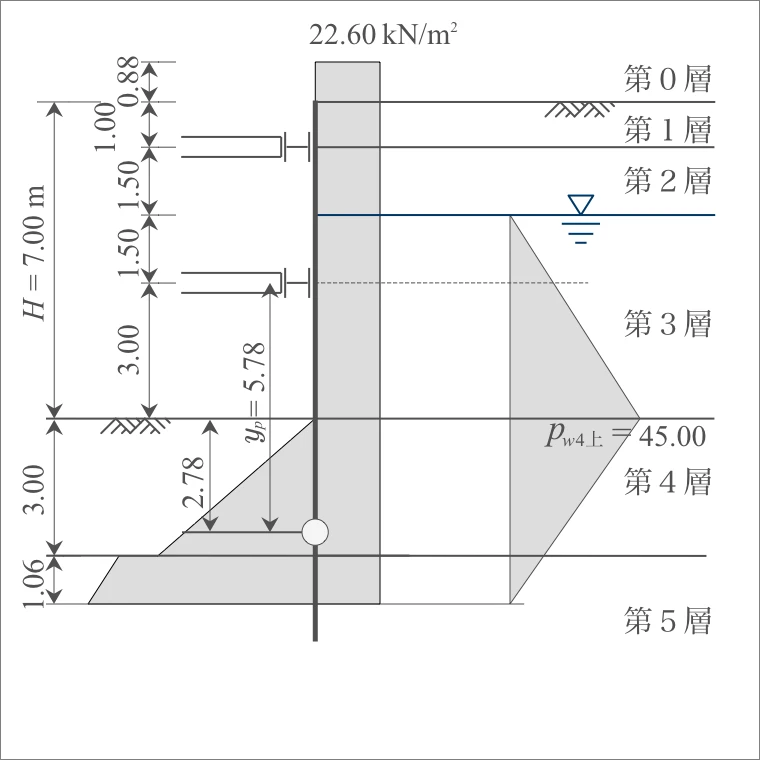
$$ \begin{equation} \begin{split} p &=a \cdot b \cdot \gamma \\[5px] &=1 \cdot 2 \cdot 11.30 \\[5px] &=22.60 \ \mathrm{kN/m^2} \end{split}\nonumber \end{equation} $$

なお、地表面での上載荷重は、平均単位体積重量を用いて「厚さ」に換算する。

$$ \begin{equation} \begin{split} 換算土圧 &=\frac{q}{\gamma} \\[5px] &=\frac{10.0}{11.30} \\[5px] &=0.88 \ \mathrm{m} \end{split}\nonumber \end{equation} $$
b. 水圧

土留めに作用する水圧は静水圧とし、掘削底面まで増加、掘削底面からつり合い深さまで減少する三角形分布とする。

c. 受働土圧

受働土圧は、根入れ長の決定に用いた値を採用する。

d. A点における反力の計算

まず、各層の主働土圧、水圧、受働土圧を合計する。

層厚
$h$
(m)		 主働土圧
$p_a$
(kN/m²)		 水圧
$p_w$
(kN/m²)		 受働土圧
$p_p$
(kN/m²)		 計
$p=p_a+p_w-p_p$
(kN/m²)
0層 上面
下面		 0.88 $p_{a0上}=22.60$
$p_{a0下}=22.60$		 - - $p_{0上}=22.60$
$p_{0下}=22.60$
1層 上面
下面		 1.00 $p_{a1上}=22.60$
$p_{a1下}=22.60$		 - - $p_{1上}=22.60$
$p_{1下}=22.60$
2層 上面
下面		 1.50 $p_{a2上}=22.60$
$p_{a2下}=22.60$		 - - $p_{2上}=22.60$
$p_{2下}=22.60$
3層 上面
下面		 4.50 $p_{a3上}=22.60$
$p_{a3下}=22.60$		 $p_{w3上}=0.00$
$p_{w3下}=45.00$		 - $p_{3上}=22.60$
$p_{3下}=67.60$
4層 上面
下面		 3.00 $p_{a4上}=22.60$
$p_{a4下}=22.60$		 $p_{w4上}=45.00$
$p_{w4下}=11.72$		 $p_{p4上}=0.00$
$p_{p4下}=81.00$		 $p_{4上}=67.60$
$p_{4下}=-46.68$
5層 上面
下面		 1.06 $p_{a5上}=22.60$
$p_{a5下}=22.60$		 $p_{w5上}=11.72$
$p_{w5下}=0.00$		 $p_{p5上}=99.63$
$p_{p5下}=134.73$		 $p_{5上}=-65.31$
$p_{5下}=-112.13$
掘削底面からp=0までの距離を$ℓ_e$とすると、
$$ \begin{equation} \begin{split} \frac{p_{4上}}{p_{4下}} &=\frac{ℓ_e}{3.00-ℓ_e} \\[5px] \frac{67.60}{46.68} &=\frac{ℓ_e}{3.00-ℓ_e} \\[5px] ℓ_e &=\frac{3.00 \times 67.60}{46.68 + 67.60} \\[5px] ℓ_e &=1.77 \ \mathrm{m} \end{split}\nonumber \end{equation} $$

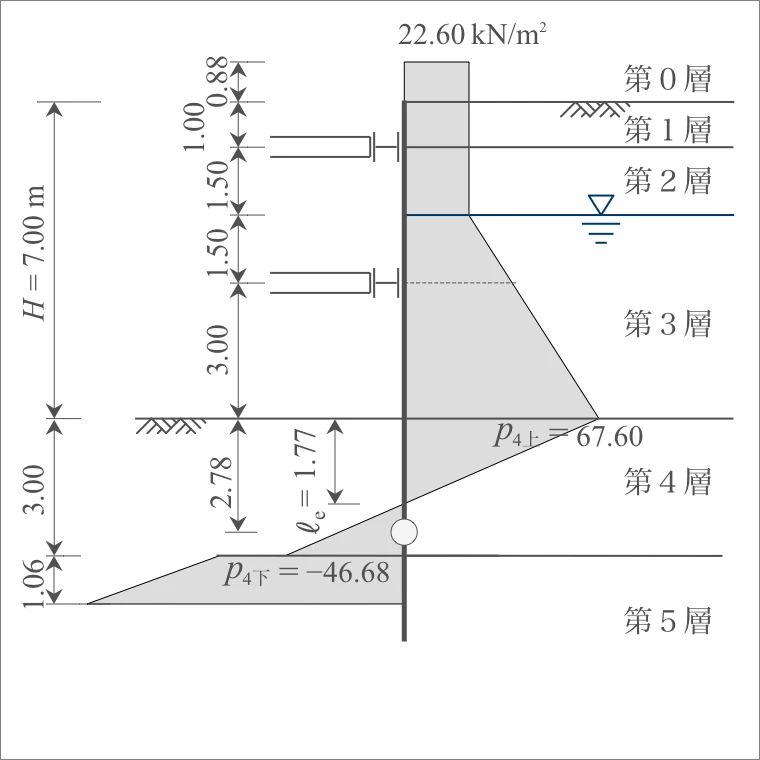
断面力の算定は、切ばりと仮想支持点を支点とする単純ばりとして計算する。

また、pが負となる作用力は無視する。

層厚
$h$
(m)
$p$
(kN/m²)
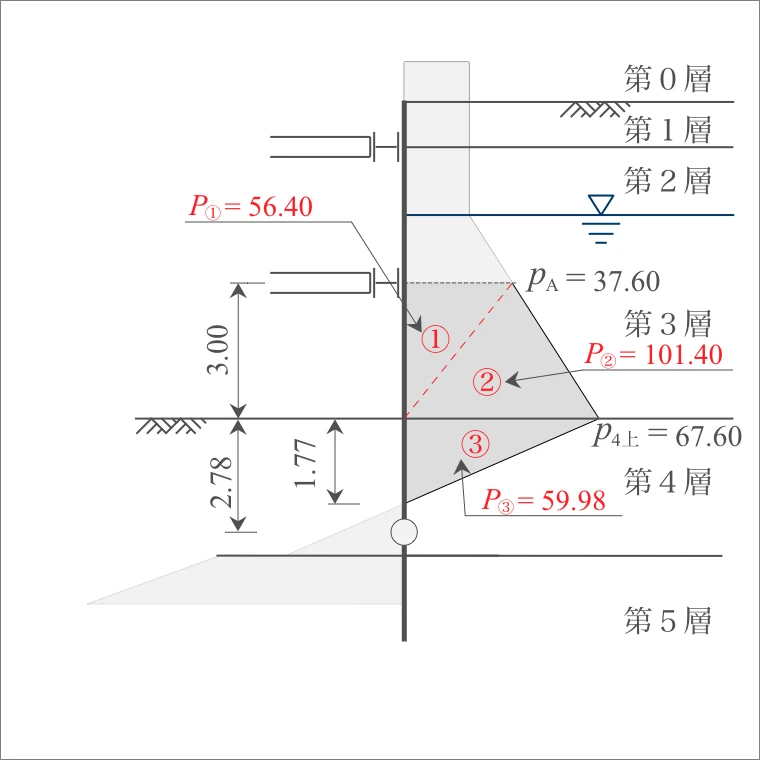
3層 A
下面		 3.00 $p_{A}=37.60$
$p_{3下}=67.60$
4層 上面
0点		 1.77 $p_{4上}=67.60$
$p_{0}=0.00$
A点（切ばり位置）から$p=0$の位置までを図のとおり、各層で分割し、その面積「側圧$P$」を求める。
計算式 側圧
$P$
(kN)
① 37.60×3.00/2= 56.40
② 67.60×3.00/2= 101.40
③ 67.60×1.77/2= 59.98
B点（仮想支持点）から各三角形の重心までの距離「アーム長$y$」を求める。
計算式 B点からのアーム長
$y$
(m)
① 2.78+3.00/3×2= 4.78
② 2.78+3.00/3×1= 3.78
③ (2.78-1.77)+1.77/3×2= 2.19

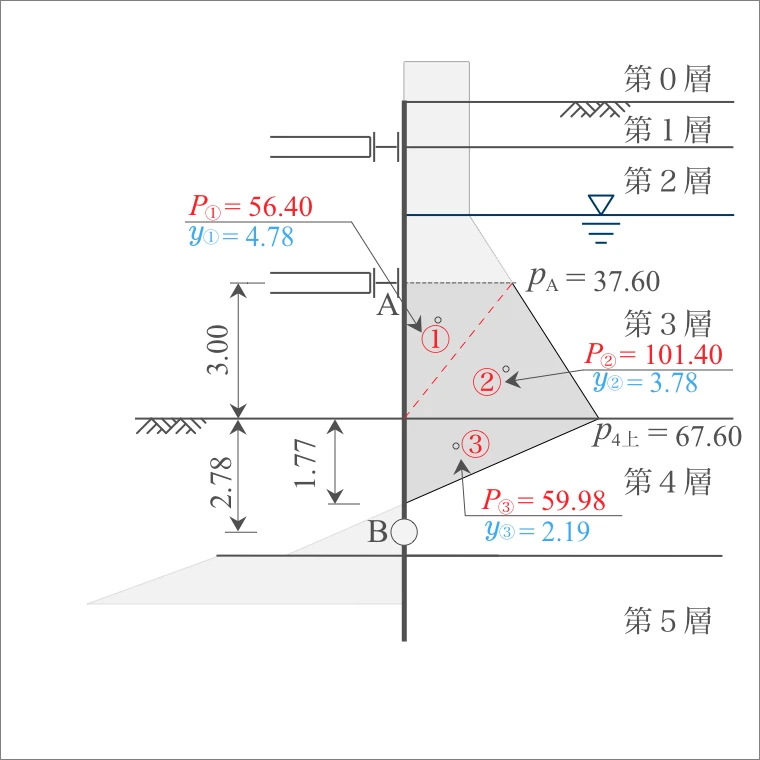
側圧$P$にアーム長$y$を乗じて、B点での作用力によるモーメント$M_B$を算出する。

側圧
$P$
(kN)		 アーム長
$y$
(m)		 モーメント
$M_B$
(kN・m)
① 56.40 4.78 269.86
② 101.40 3.78 383.78
③ 59.98 2.19 131.56
∑ 785.20

よって、A点（切ばり位置）における反力$R_A$は、B点でのモーメントのつり合いより、

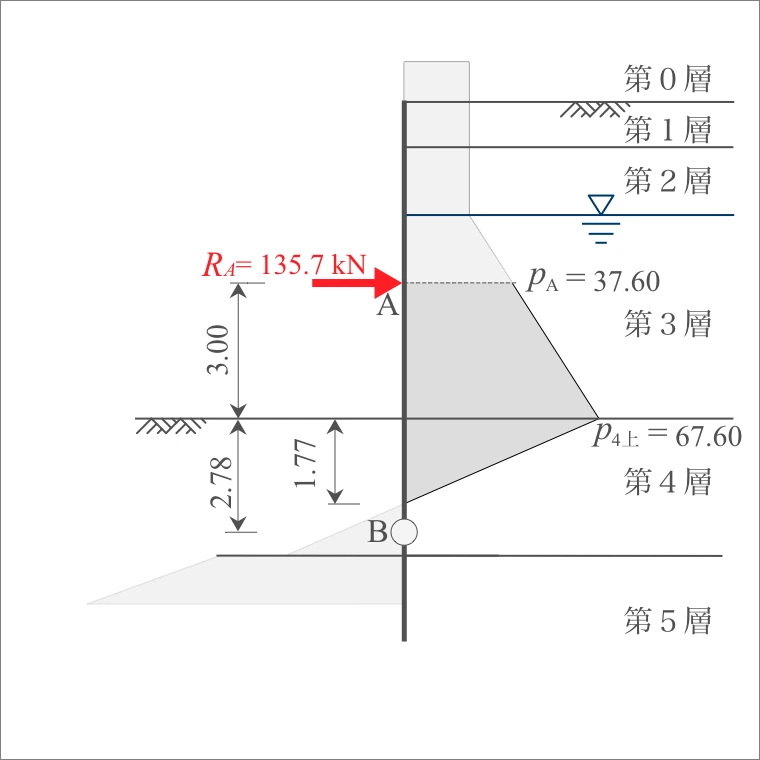
$$(A点からB点までの距離)\times R_A = \sum M_B$$ $$(2.78 + 3.00)\times R_A=785.20$$ よって、切ばり位置における反力は $$R_A=135.7\ \mathrm{kN}$$
(2) 土圧・水圧による曲げモーメント

最大曲げモーメントは「３層」で発生すると想定されるので、A点から下方向に距離 「$x$」 を定義し、その「$x$」から上部方向における曲げモーメントを計算する。

📌NOTE
  • 最大曲げモーメントの発生位置をある程度想定した方が計算が簡単になります。
  • もし、計算結果が「３層」に収まらない場合は、別の層で再度計算することになります。
A点（切ばり位置）から$x$の位置までを図のとおり、各層で分割する。
層厚
$h$
(m)		 計
$p$
(kN/m²)
3層 A
$x$		 3.00 $p_{A}=$ 37.60
$p_{x}=$ 10 $x$ +37.60
$x$
下面		 $p_{x}=$ 10 $x$ +37.60
$p_{3下}=$67.60

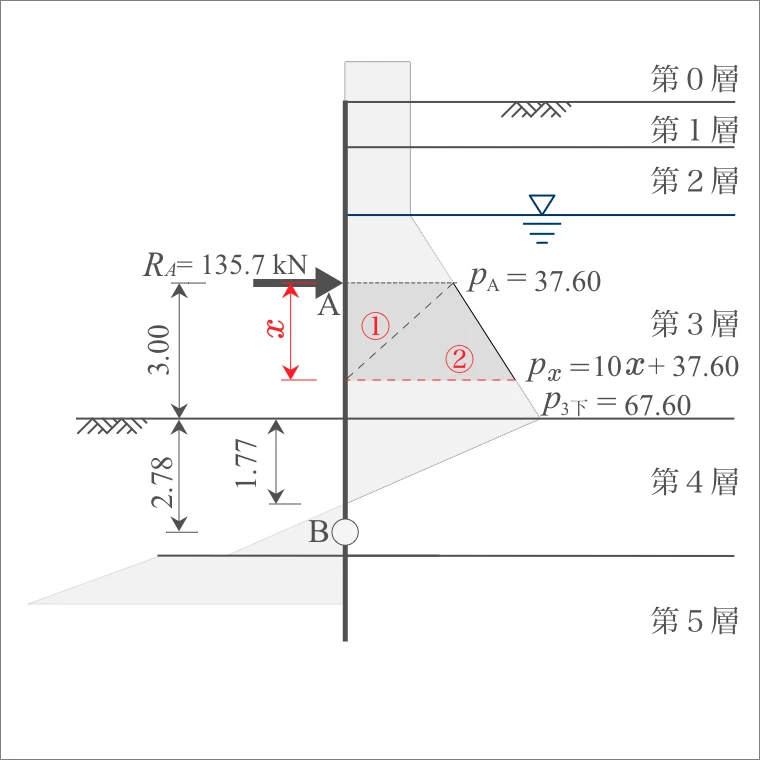
ここで、

$$ \begin{equation} \begin{split} p_x &=\frac{(67.60 - 37.60)}{3.00} x + 3.60\\[5px] &=10 x + 37.60 \end{split}\nonumber \end{equation} $$
分割した箇所のそれそれの面積「側圧$P$」を求める。
計算式 側圧
$P$
(kN)
① 37.60× $x$ /2= 18.80 $x$
② (10 $x$ +37.60)× $x$ /2= 5.00 $x^2$ 18.80 $x$
$x$点から各三角形の重心までの距離「アーム長$y$」を求める。
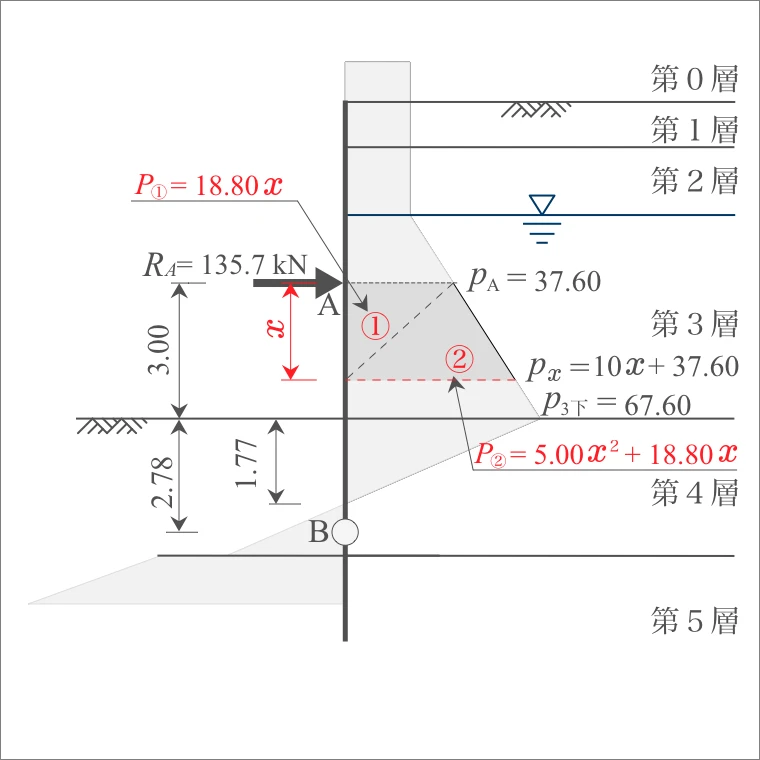
計算式
$x$点から重心の鉛直距離		 アーム長
$y$
(m)
① $x$ /3×2= 0.67 $x$
② $x$ /3×1= 0.33 $x$

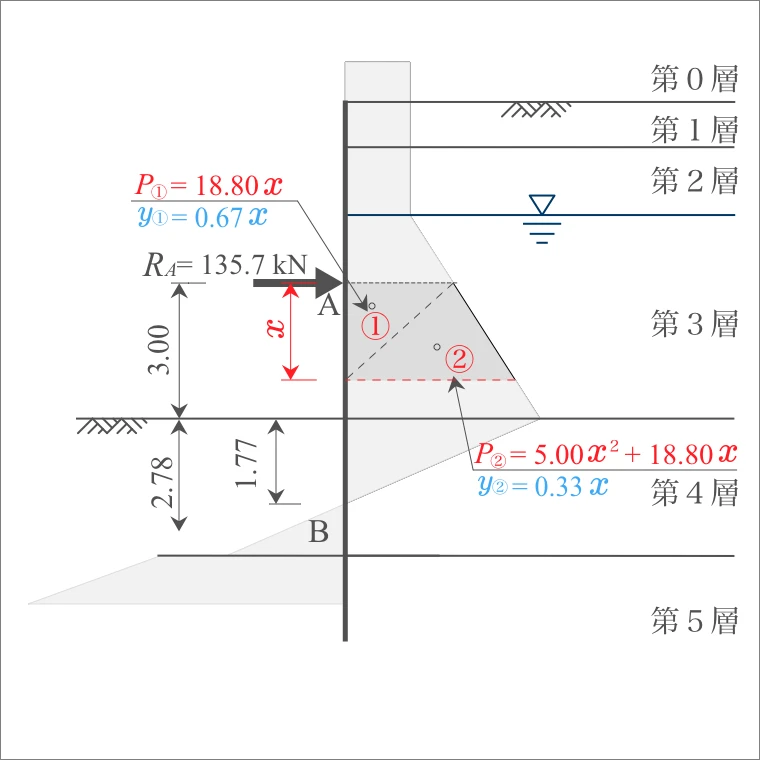
モーメント$M$は、「側圧 $P$」に「アーム長$y$」を乗じて算出する。

$$ M = P \cdot y $$

表計算すると下記のとおり。

側圧
$P$
(kN)		 アーム長
$y$
(m)		 作用モーメント
$M$
(kN・m)
3層 ① 18.80 $x$ 0.67 $x$ 12.53 $x^2$
② 5.00 $x^2$ 18.80 $x$ 0.33 $x$ 1.67 $x^3$ + 6.27 $x^2$
$\sum M=$ 1.67 $x^3$ +18.80 $x^2$

以上より、作用モーメントは下式のとおりとなる。

$$ \sum M= 1.67 x^3 +18.80 x^2 $$
(3) 最大曲げモーメント

(1),(2)より、任意点ｘでの曲げモーメントは、下式のとおりとなる。

$$ \begin{equation} \begin{split} M_x &=R_A \cdot x -(1.67 x^3+ 18.80 x^2) \\[5px] &=135.7 \cdot x -(1.67x^3+18.80 x^2) \\[5px] &=-1.67x^3 -18.80x^2+135.7x \end{split} \nonumber \end{equation} $$

微分すると、

$$ M_x ^\prime =-5.00x^2 -37.60x+135.7 \nonumber $$

最大曲げモーメントの位置は、上式=0となるため、

$$ \begin{equation} \begin{split} x &=\frac{37.60- \sqrt{37.60^2 - 4 \times -5.00 \times 135.7}}{2 \times -5.00}\\[5px] &=2.67\ \mathrm{m} \end{split} \nonumber \end{equation} $$

よって、最大曲げモーメントの値は、

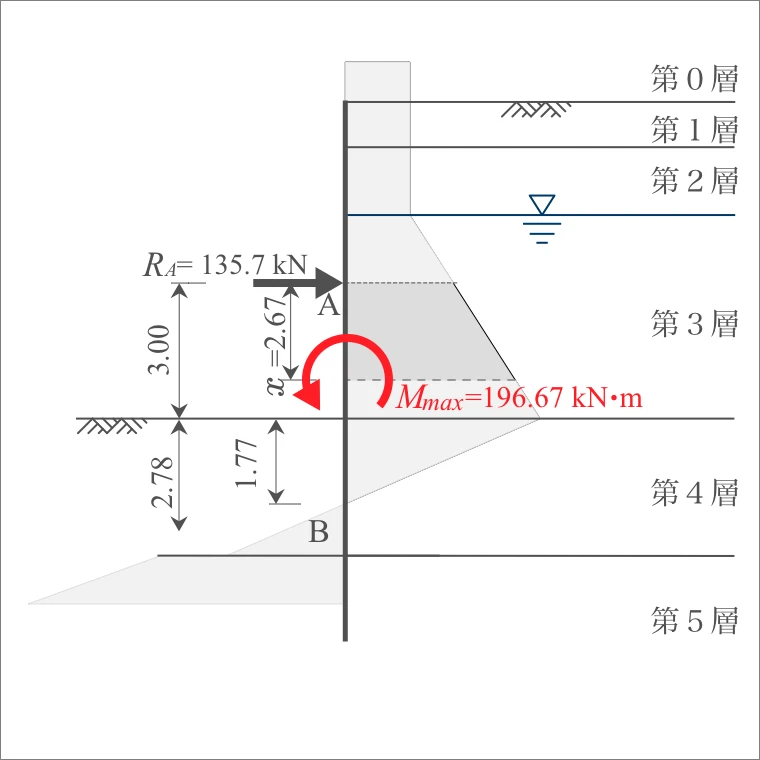
$$ \begin{equation} \begin{split} M_{max} &=-1.67 \times 2.67^3 - 18.80 \times 2.67^2 + 135.7 \times 2.67\\[5px] &=196.67\ \mathrm{kN・m} \end{split} \nonumber \end{equation} $$

3-2-3. 曲げ応力度の照査

鋼矢板に発生する最大曲げ応力度が、許容応力度以下であれば「OK」と判定し、「4. 変位量の検討」に進む。
許容応力度をを超えた場合は「NG」と判定し、「1-3. 鋼矢板の設定」に戻り、鋼矢板の型式を上げる。（H11道仮p.109）

$$ \sigma_{max}=\frac{M_{max}}{Z \cdot e} \nonumber $$

ここに、

  • $\sigma_{max}$：鋼矢板に発生する最大曲げ応力度（N/mm²）
  • $Z$：断面係数（m³/m）$Z=1,340.0\ \mathrm{cm^3/m}=0.0013400\ \mathrm{m^3/m}$
  • $e$：断面係数の有効率（応力度の計算）$e=60\%$

よって、

$$ \begin{equation} \begin{split} \sigma_{max} &=\frac{196.67}{0.0013400 \cdot 0.6}\\[5px] &=244,610\ \mathrm{kN/m^2}\\[5px] &=244.6\ \mathrm{N/mm^2} \leqq \sigma_{sa}=270.0\ \mathrm{N/mm^2} \ \mathrm{OK} \end{split}\nonumber \end{equation} $$

4.変位量の検討（鋼矢板の剛性の検討）

4-1. 単純ばりのスパン

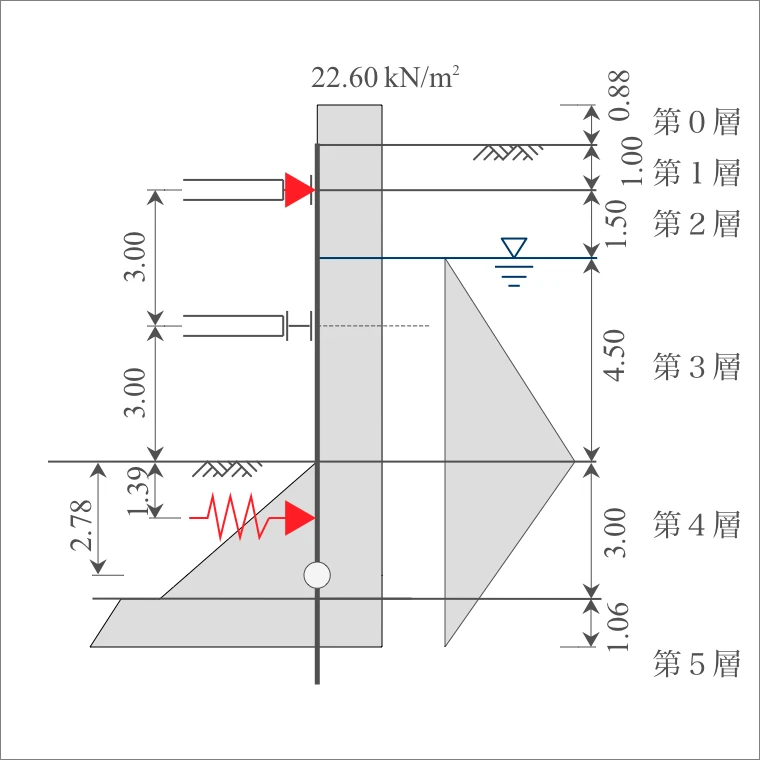
鋼矢板は、最上段切ばり位置を剛な支点とし、仮想支持点深さの1/2の点を弾性支点として、その間を単純ばりとする。（H11道仮p.92） 単純ばりのスパン$ℓ_1$は、
$$ \begin{equation} \begin{split} ℓ_1 &=3.00+3.00+2.78/2 \\[5px] &=3.00+3.00+1.39 \\[5px] &=7.39\ \mathrm{m} \end{split}\nonumber \end{equation} $$

4-2. 荷重の計算

荷重は、断面決定用の土圧と水圧をスパン全長にわたり載荷する。ただし、全載荷重をスパンで除した荷重強度を算出し、等価な長方形分布荷重とする。（H11道仮p.92）

2層から5層までの作用力と層厚は、表のとおりである。

層厚
$h$
(m)		 主働土圧
$p_a$
(kN/m²)		 水圧
$p_w$
(kN/m²)		 受働土圧
$p_p$
(kN/m²)
2層 上面
下面		 1.50 $p_{a2上}=22.60$
$p_{a2下}=22.60$		 - -
3層 上面
下面		 4.50 $p_{a3上}=22.60$
$p_{a3下}=22.60$		 $p_{w3上}=0.00$
$p_{w3下}=45.00$		 -
4層 上面
下面		 3.00 $p_{a4上}=22.60$
$p_{a4下}=22.60$		 $p_{w4上}=45.00$
$p_{w4下}=11.72$		 $p_{p4上}=0.00$
$p_{p4下}=81.00$
5層 上面
下面		 1.06 $p_{a5上}=22.60$
$p_{a5下}=22.60$		 $p_{w5上}=11.72$
$p_{w5下}=0.00$		 $p_{p5上}=99.63$
$p_{p5下}=134.73$

受働土圧は無視する。単純張りの範囲の作用力は下記のとおりとなる。

層厚
$h$
(m)		 主働土圧
$p_a$
(kN/m²)		 水圧
$p_w$
(kN/m²)		 計
$p=p_a+p_w$
(kN/m²)
2層 上面
下面		 1.50 $p_{a2上}=22.60$
$p_{a2下}=22.60$		 - $p_{2上}=22.60$
$p_{2下}=22.60$
3層 上面
下面		 4.50 $p_{a3上}=22.60$
$p_{a3下}=22.60$		 $p_{w3上}=0.00$
$p_{w3下}=45.00$		 $p_{3上}=22.60$
$p_{3下}=67.60$
4'層 上面
下面		 1.39 $p_{a4上}=22.60$
$p_{a4'下}=22.60$		 $p_{w4上}=45.00$
$p_{w4'下}=29.55$		 $p_{4上}=67.60$
$p_{4'下}=52.15$
各層の側圧$P$を求める。
計算式 側圧
$P$
(kN/m²)
2層 22.60×1.50= 33.90
3層 (22.60+67.60)×4.50/2= 202.95
4'層 (67.60+52.15)×1.39/2= 83.38
$\sum P$ 320.22
全載荷重をスパンで除して、分布荷重$W$を求める。
$$ \begin{equation} \begin{split} W &= \frac{\sum P}{ℓ_1} \\[5px] &= \frac{320.22}{7.39} \\[5px] &=43.32\ \mathrm{kN/m} \end{split}\nonumber \end{equation} $$

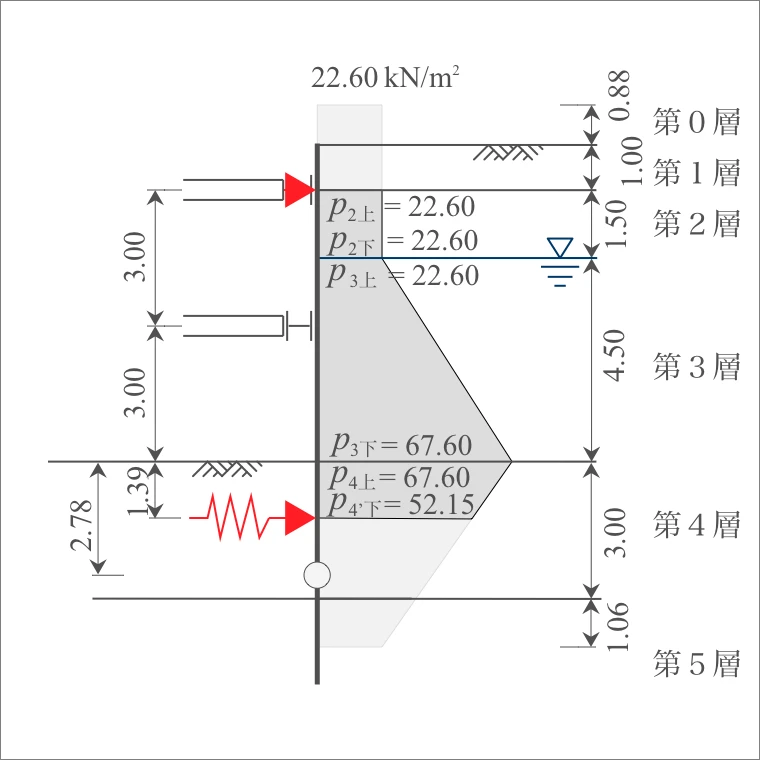
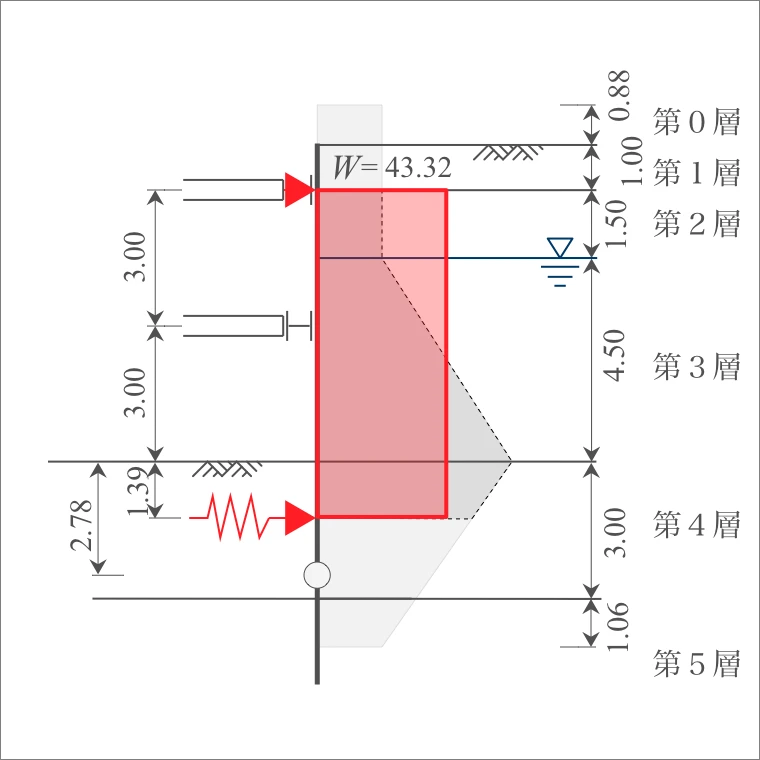
4-3. 変位量の照査

変位量δは、単純ばり中央の最大たわみ$\delta_1$と、その最大たわみが生じる点における弾性支点の変位の影響$\delta_2$との合計として求める。

4-3-1. 単純ばり中央の最大たわみδ₁

$$ \begin{equation} \begin{split} \delta_1 &= \frac{5Wℓ^4}{384EIK_I} \\[5px] &= \frac{5 \times 43.32 \times 7.39^4}{384 \times 200,000,000 \times 0.000168 \times 0.45} \\[5px] &=\textcolor{red}{0.1114}\ \mathrm{m} \end{split}\nonumber \end{equation} $$

ここに、

  • $W$：分布荷重 $W = 43.32\ \mathrm{N/mm^2}$
  • $ℓ$：単純ばりのスパン長 $ℓ = 7.39\ \mathrm{m}$
  • $E$：ヤング係数 $E = 200,000\ \mathrm{N/mm^2}$ （1-2. 鋼矢板の設定より）
  • $I$：断面二次モーメント $I= 16,800\ \mathrm{cm^4/m}$ （1-2. 鋼矢板の設定より）
  • $K_I$：断面二次モーメントの有効率（断面力、変位の計算）：$K_I=45$% （1-2. 鋼矢板の設定より）

4-3-2. 弾性支点の変位の影響δ₂

$$ \begin{equation} \begin{split} \delta_2 &= \frac{0.5 \cdot W \cdot ℓ}{2 \cdot k_h \cdot h_p} \\[5px] &= \frac{0.5 \times 43.32 \times 7.39}{2 \times 10,091.81 \times 2.78 \times 1.00} \\[5px] &=\textcolor{red}{0.0028}\ \mathrm{m} \end{split}\nonumber \end{equation} $$

ここに、

  • $k_h$：水平方向地盤反力係数(kN/m³)
$$ \begin{equation} \begin{split} k_h &= \eta \cdot k_{h0} \left( \frac{B_H}{0.3} \right)^{-3/4} \\[5px] &= 1 \times 140,000 \left( \frac{10}{0.3} \right)^{-3/4} \\[5px] &=10,092 \end{split}\nonumber \end{equation} $$
  • $\eta$：壁体形式に関わる係数 $\eta=1$
  • $k_{H0}$：直径30cmの剛体円板による平板載荷試験の値に相当する水平方向地盤反力係数(kN/m³)
$$ \begin{equation} \begin{split} k_{h0} &= \frac{1}{0.3} \alpha \cdot E_0 \\[5px] &= \frac{1}{0.3} \cdot 1 \cdot 420,000 \\[5px] &=140,000 \end{split}\nonumber \end{equation} $$
  • $\alpha$：地盤反力係数の推定に用いる係数 $\alpha=1$
  • $E_0$：測定または推定した設計の対象とする位置での地盤の変形係数(kN/m²)
$$ \begin{equation} \begin{split} E_0 &= 2,800 \cdot N \\[5px] &= 2,800 \cdot 15 \\[5px] &= 42,000 \end{split}\nonumber \end{equation} $$
  • $N$：各層の「標準貫入試験のN値」の平均値 $N=15$
  • $B_H$：換算載荷幅 $B_H=10 \ \mathrm{m}$
  • $h_p$：仮想支持点の深さ(m) $h_p=2.78$
  • $B$：鋼矢板の単位幅 $B=1 \ \mathrm{m}$

4-3-3. 変位量δの照査

$$ \begin{equation} \begin{split} \delta &= \delta_1 + \delta_2 \\[5px] &= 0.1114 + 0.0028 \\[5px] &= 0.1142 \leqq \delta_a=0.30\ \mathrm{m} \ \mathrm{OK} \end{split}\nonumber \end{equation} $$

5. 腹起しの設計

H11道仮p.116に従い、腹起しの設計は、「一般部」と「端部」のそれぞれを設計する。

5-1. 一般部

5-1-1. 荷重の計算

支保工の設計に用いる荷重は、断面決定用土圧と水圧とし、最終掘削状態において各段の支保工に下方分担法により作用させる。（H11道仮p.35）

層厚
$h$
(m)		 計
$p$
(kN/m²)
0層 上面
下面		 0.88 $p_{0上}=$ 22.60
$p_{0下}=$ 22.60
1層 上面
下面		 1.00 $p_{1上}=$ 22.60
$p_{1下}=$ 22.60
2層 上面
下面		 1.50 $p_{2上}=$ 22.60
$p_{2下}=$ 22.60
3層 上面
A		 1.50 $p_{3上}=$ 22.60
$p_{A}=$ 37.60
A
下面		 3.00 $p_{A}=$ 37.60
$p_{3下}=$ 67.60

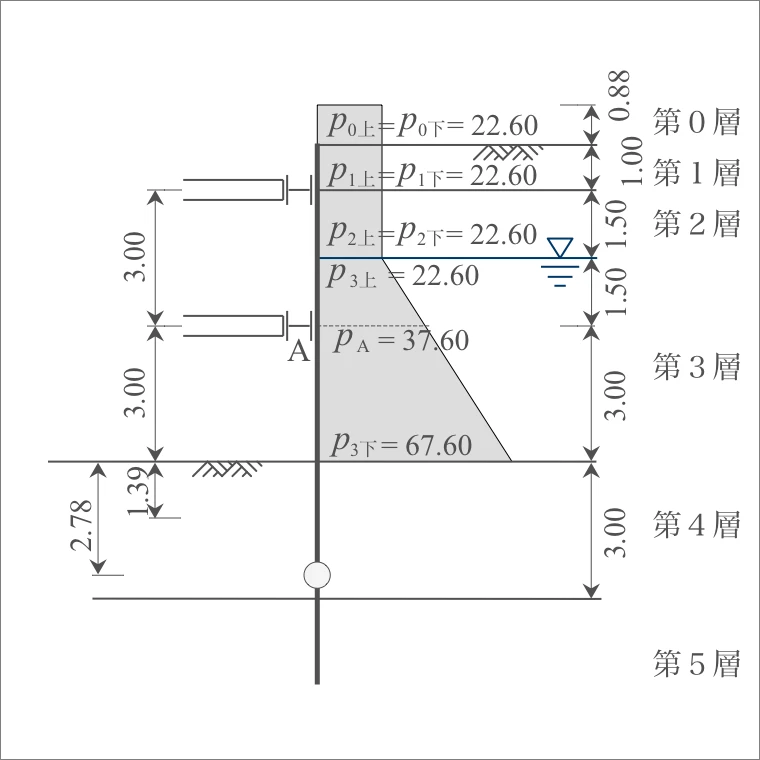
上段の切ばりに分担させる側圧は、上からA点（下段の切ばり）までとなる。

計算式 側圧
$P$
(kN)
0層 22.60×0.88= 20.00
1層 22.60×1.00= 22.60
2層 22.60×1.50= 33.90
3層 (22.60 + 37.60) ×1.50 /2 = 45.15
$\sum$ 121.65
よって、上段の「単位長さあたりの支保工反力」は
$$ R_1 = 121.65 \ \mathrm{kN/m} $$

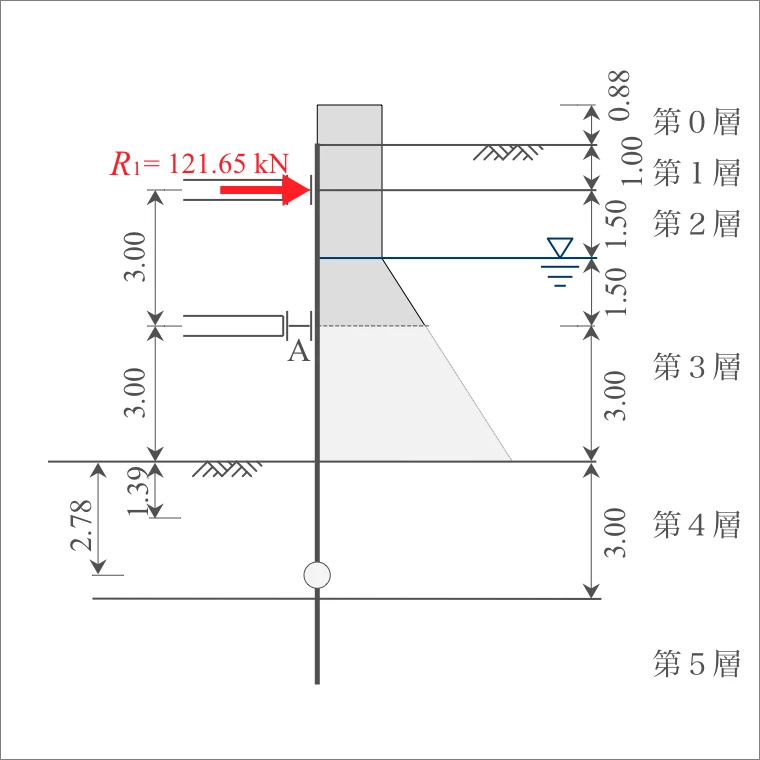
下段の切ばりに分担させる側圧は、A点（下段の切ばり）から掘削底面までとなる。

計算式 側圧
$P$
(kN)
3層 (37.60 + 67.60) ×3.00 /2 = 157.80
$\sum$ 157.80
よって、下段の「単位長さあたりの支保工反力」は
$$ R_2 = 157.80 \ \mathrm{kN/m} $$

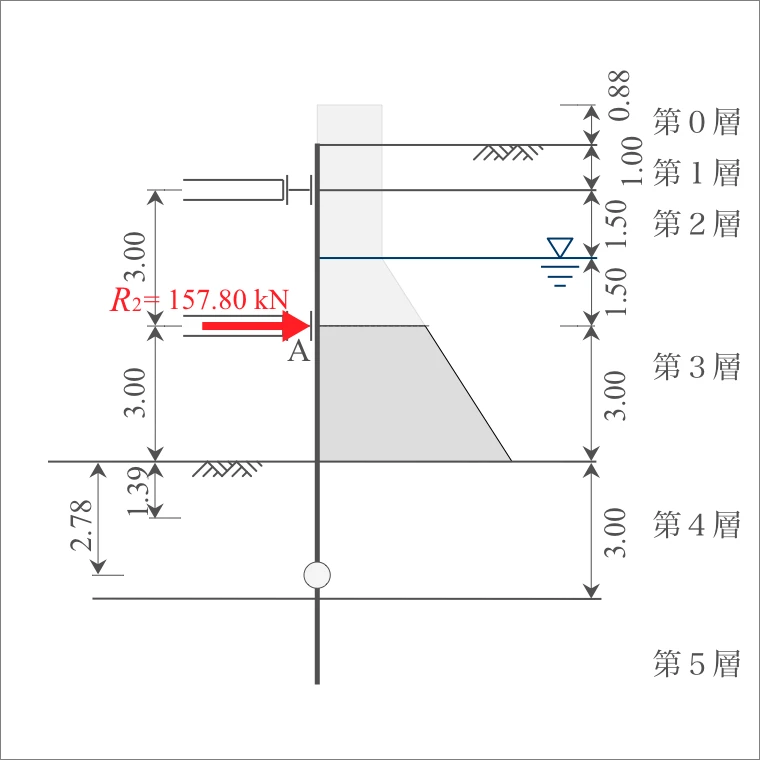
5-1-2. 断面力の計算

(1) 諸条件の計算

腹起しを設計する際の荷重の載荷方法は、単位長さ当りの支保工反力Rを等分布荷重として載荷する。そして、切ばりの水平間隔Bから火打ちを差し引いた長さを支間（スパン）とする単純ばりとして断面力を計算する。（H11道仮p118,119）

切ばりの水平間隔 $B=5.00 \ \mathrm{m}$
火打ちの腹起し方向の幅 $ℓ_2=1.50 \ \mathrm{m}$
火打ち間の幅 $ℓ_1 = B - 2 \cdot ℓ_2$ $= 5.00 - 2 \times 1.50$ $= 2.00\ \mathrm{m}$
火打ちの角度 $\theta =45 \ \mathrm{度}$
よって、H11道仮p118より、支間は
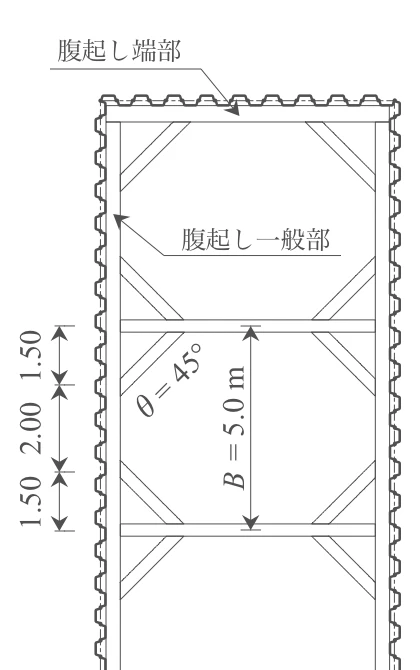
$$ \begin{equation} \begin{split} ℓ &= ℓ_1 + ℓ_2 \\[5px] &= 2.00 + 1.50 \\[5px] &= 3.50\ \mathrm{m} \end{split}\nonumber \end{equation} $$

また、一般部においても、軸力が作用する腹起し材であるため、曲げと圧縮を受ける部材として設計する。

火打ちの腹起し方向の幅（妻部） $ℓ_4=2.00 \ \mathrm{m}$

火打ち間の幅（妻部）
$$ \begin{equation} \begin{split} ℓ_3 &= B_e - 2 \cdot h - 2 \cdot ℓ_4 \\[5px] &= 7.20 - 2 \times 0.10 - 2 \times 2.00 \\[5px] &= 3.00\ \mathrm{m} \end{split}\nonumber \end{equation} $$
よって、軸力を考慮する腹起しの軸力分担幅は、
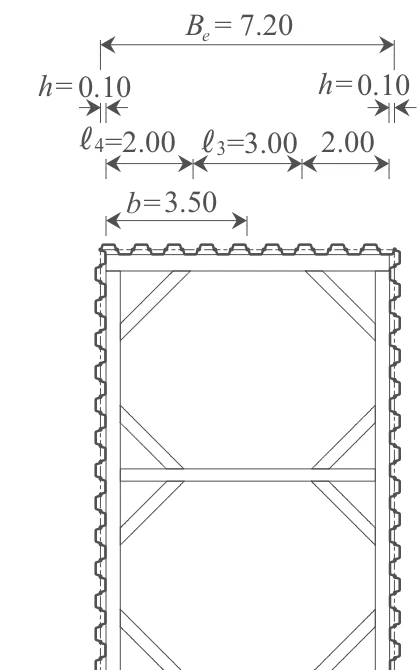
$$ \begin{equation} \begin{split} b &= \frac{1}{2} \cdot ℓ_3 + ℓ_4 \\[5px] &= \frac{1}{2} \times 3.00 + 2.00 \\[5px] &= 3.50\ \mathrm{m} \end{split}\nonumber \end{equation} $$

温度変化に伴う軸力増加は$\Delta N = 150 \ \mathrm{kN}$ とする。

(2) 上段

＜軸力＞

$$ \begin{equation} \begin{split} N_1 &= (R_1 \cdot b + \Delta N) / 本数 \\[5px] &= (121.65 \times 3.50 + 150) /1 \\[5px] &= 575.76\ \mathrm{kN} \end{split}\nonumber \end{equation} $$

＜最大曲げモーメント＞

$$ \begin{equation} \begin{split} M_{max1} &= \frac{R_1 \cdot ℓ^2}{8} \times \frac{1}{本数} \\[5px] &= \frac{121.65 \times 3.50^2}{8} \times \frac{1}{1} \\[5px] &= 186.27\ \mathrm{kN・m} \end{split}\nonumber \end{equation} $$

＜最大せん断力＞

$$ \begin{equation} \begin{split} S_{max1} &= \frac{R_1 \cdot ℓ}{2} \times \frac{1}{本数} \\[5px] &= \frac{121.65 \times 3.50}{2} \times \frac{1}{1} \\[5px] &= 212.88\ \mathrm{kN・m} \end{split}\nonumber \end{equation} $$
(3) 下段

＜軸力＞

$$ \begin{equation} \begin{split} N_2 &= (R_2 \cdot b + \Delta N) / 本数 \\[5px] &= (157.80 \times 3.50 + 150) /1 \\[5px] &= 702.29\ \mathrm{kN} \end{split}\nonumber \end{equation} $$

＜最大曲げモーメント＞

$$ \begin{equation} \begin{split} M_{max2} &= \frac{R_2 \cdot ℓ^2}{8} \times \frac{1}{本数} \\[5px] &= \frac{157.80 \times 3.50^2}{8} \times \frac{1}{1} \\[5px] &= 241.63\ \mathrm{kN・m} \end{split}\nonumber \end{equation} $$

＜最大せん断力＞

$$ \begin{equation} \begin{split} S_{max2} &= \frac{R_2 \cdot ℓ}{2} \times \frac{1}{本数} \\[5px] &= \frac{157.80 \times 3.50}{2} \times \frac{1}{1} \\[5px] &= 276.14\ \mathrm{kN・m} \end{split}\nonumber \end{equation} $$

5-1-3. 応力度の照査（上段）

(1) 安定の照査

照査は、２つの照査式で行う。（H11道仮p50）

照査式（2-6-1）

$$ \begin{equation} \begin{split} \frac{\sigma_c}{\sigma_{caz}}+\frac{\sigma_{bcy}}{\sigma_{bagy}(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{\sigma_{bao}(1-\frac{\sigma_c}{\sigma_{eaz}})} \leqq 1 \end{split} \nonumber \end{equation} $$

照査式（2-6-2）

$$ \sigma_c+\frac{\sigma_{bcy}}{(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{(1-\frac{\sigma_c}{\sigma_{eaz}})} \leqq \sigma_{caℓ} \nonumber $$

ここに、

  • $\sigma_c$：照査する断面に作用する軸方向力による圧縮応力度（N/mm²）
    • $\displaystyle \sigma_c=\frac{N}{A}=\frac{575.8 \times 1,000}{154.90 \times 100}=37.2\ \mathrm{N/mm^2}$
  • $\sigma_{bcy}$：強軸まわりに作用する曲げモーメントによる曲げ圧縮応力度（N/mm²）
    • $\displaystyle \sigma_{bcy}=\frac{M_{max}}{Z}=\frac{186.3 \times 1,000,000}{2,000 \times 1,000}=93.1\ \mathrm{N/mm^2}$
  • $\sigma_{bcz}$：弱軸まわりに作用する曲げモーメントによる曲げ圧縮応力度（N/mm²）
    • $\displaystyle \sigma_{bcz}=0$
  • $\sigma_{caz}$：弱軸まわりの許容軸方向圧縮応力度（N/mm²）
    • ただし、$b ^\prime \leqq 13.1\ t ^\prime$ とする
    • $b ^\prime$：切ばりのフランジ片幅
      • $b ^\prime = ( 350-12)/2=169 \ \mathrm{mm}$
    • $t ^\prime$：切ばりのフランジ厚
      • $t ^\prime = 19 \ \mathrm{mm}$
    • $ℓ_z$：切ばりの弱軸まわりの座屈長（水平方向座屈長）
      • $ℓ_z=3.50 \ \mathrm{m}$（H11道仮p122より）
    • よって、弱軸の細長比は、
      • $\displaystyle \frac{ℓ_z}{r_z}=\frac{3.50 \times 1,000}{8.99 \times 10}=38.9$
    • よって、軸方向圧縮の計算式は、18<ℓ/r≦92 より（H11道仮p.47）
$$ \begin{equation} \begin{split} \sigma_{caz}&=[140-0.82(ℓ/r_z-18)]\times 1.5\\[5px] &=[140-0.82(38.9-18)]\times1.5\\[5px] &=184.3\ \mathrm{N/mm^2} \end{split}\nonumber \end{equation} $$
  • $\sigma_{bagy}$：局部座屈を考慮しない強軸まわりの許容曲げ圧縮応力度（N/mm²）
    • ただし、$2A_c \geqq A_w$
    • $A_c$：圧縮フランジの総断面積
      • $A_c=350 \times 19 = 6,650\ \mathrm{mm^2}$
    • $A_w$：ウェブの総断面積
      • $A_w=(350 - 2 \times 19) \times 12 = 3,744\ \mathrm{mm^2}$
    • $ℓ_y$：フランジ間の固定間距離（鉛直方向座屈長）
      • $ℓ_y=3.50\ \mathrm{m}$（H11道仮p.122）
    • よって、$ℓ/b$は、
      • $\displaystyle \frac{ℓ_y}{b}=\frac{3.50 \times 1,000}{350}=10.0$
    • よって、曲げ圧縮縁の計算式は、4.5 <$ℓ/b$≦30より(H11道仮p47)
$$ \begin{equation} \begin{split} \sigma_{bagy}&=\{140 - 2.4 ( ℓ_y / b - 4.5)\} \times 1.5\\[5px] &=\{140 - 2.4 ( 10.0 - 4.5)\} \times 1.5\\[5px] &=190.2 \ \mathrm{N/mm^2} \end{split} \nonumber \end{equation} $$
  • $\sigma_{ba0}$：局部座屈を考慮しない許容曲げ圧縮応力度の上限値
    • $\sigma_{ba0}=210 \ \mathrm{N/mm^2}$（H11道仮p51）
  • $\sigma_{caℓ}$：圧縮応力を受ける自由突出板の局部座屈に対する許容応力度
    • $\sigma_{caℓ}=210 \ \mathrm{N/mm^2}$（H11道仮p51）
    • ただし、$b ^\prime \leqq 13.1\ t ^\prime$とする。
  • $\sigma_{eay}$, $\sigma_{eaz}$：それぞれ強軸および弱軸まわりのオイラー座屈応力度（N/mm²） (H11道仮p51)
    • $\displaystyle \sigma_{eay}=\frac{1,200,000}{(ℓ ^\prime / r_y)^2}=\frac{1,200,000}{(3,500/151.0)^2}=\frac{1,200,000}{537.3}=2,233.6\ \mathrm{N/mm^2}$
    • $\displaystyle \sigma_{eaz}=\frac{1,200,000}{(ℓ ^\prime / r_z)^2}=\frac{1,200,000}{(3,500/89.9)^2}=\frac{1,200,000}{1,515.7}=791.7\ \mathrm{N/mm^2}$
      • $ℓ ^\prime$：材料両端の支点条件より定まる有効座屈長（mm）
      • $ℓ ^\prime=3.50 \times 1,000 = 3,500\ \mathrm{mm}$
      • $r_y, r_z$：それぞれ強軸および弱軸まわりの断面二次半径（mm）
      • $r_y=15.10 \times 10 = 151.0\ \mathrm{mm}$
      • $r_z=8.99 \times 10 = 89.9\ \mathrm{mm}$

よって、
照査式(2-6-1)

$$ \begin{equation} \begin{split} \frac{\sigma_c}{\sigma_{caz}}&+\frac{\sigma_{bcy}}{\sigma_{bagy}(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{\sigma_{bao}(1-\frac{\sigma_c}{\sigma_{eaz}})}\\[5px] &= \frac{37.2}{184.3}+\frac{93.1}{190.2(1-\frac{37.2}{2,233.6})}+\frac{0.0}{210.0(1-\frac{37.2}{791.7})} \\[5px] &=0.20+0.50+0.00\\[5px] &=0.70\leqq 1 \ \ \mathrm{OK} \end{split} \nonumber \end{equation} $$

照査式（2-6-2）

$$ \begin{equation} \begin{split} \sigma_c&+\frac{\sigma_{bcy}}{(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{(1-\frac{\sigma_c}{\sigma_{eaz}})} \\[5px] &=37.2+\frac{93.1}{(1-\frac{37.2}{2,233.6})}+\frac{0.0}{(1-\frac{37.2}{791.7})} \\[5px] &=37.2+94.7+0.0 \\[5px] &=131.9 \leqq \sigma_{caℓ}＝210.0 \ \ \mathrm{OK} \end{split} \nonumber \end{equation} $$
(2) せん断力の照査

最大せん断力をウェブの面積で除して求める。

$$ \begin{equation} \begin{split} \tau &= \frac{S_{max1}}{A_w} \\[5px] &= \frac{212.88 \times 1,000}{(350 - 2 \times 19)\times 12} \\[5px] &= 56.9 \leqq \tau_a＝120.0 \ \ \mathrm{OK} \end{split} \nonumber \end{equation} $$

5-1-4. 応力度の照査（下段）

(1) 安定の照査

照査は、２つの照査式で行う。（H11道仮p50）

照査式（2-6-1）

$$ \begin{equation} \begin{split} \frac{\sigma_c}{\sigma_{caz}}+\frac{\sigma_{bcy}}{\sigma_{bagy}(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{\sigma_{bao}(1-\frac{\sigma_c}{\sigma_{eaz}})} \leqq 1 \end{split} \nonumber \end{equation} $$

照査式（2-6-2）

$$ \sigma_c+\frac{\sigma_{bcy}}{(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{(1-\frac{\sigma_c}{\sigma_{eaz}})} \leqq \sigma_{caℓ} \nonumber $$

ここに、

  • $\sigma_c$：照査する断面に作用する軸方向力による圧縮応力度（N/mm²）
    • $\displaystyle \sigma_c=\frac{N}{A}=\frac{702.3 \times 1,000}{154.90 \times 100}=45.3\ \mathrm{N/mm^2}$
  • $\sigma_{bcy}$：強軸まわりに作用する曲げモーメントによる曲げ圧縮応力度（N/mm²）
    • $\displaystyle \sigma_{bcy}=\frac{M_{max}}{Z}=\frac{241.6 \times 1,000,000}{2,000 \times 1,000}=120.8\ \mathrm{N/mm^2}$
  • $\sigma_{bcz}$：弱軸まわりに作用する曲げモーメントによる曲げ圧縮応力度（N/mm²）
    • $\displaystyle \sigma_{bcz}=0$
  • $\sigma_{caz}$：弱軸まわりの許容軸方向圧縮応力度（N/mm²）
    • ただし、$b ^\prime \leqq 13.1\ t ^\prime$ とする
    • $b ^\prime$：切ばりのフランジ片幅
      • $b ^\prime = ( 350-12)/2=169 \ \mathrm{mm}$
    • $t ^\prime$：切ばりのフランジ厚
      • $t ^\prime = 19 \ \mathrm{mm}$
    • $ℓ_z$：切ばりの弱軸まわりの座屈長（水平方向座屈長）
      • $ℓ_z=3.50 \ \mathrm{m}$（H11道仮p122より）
    • よって、弱軸の細長比は、
      • $\displaystyle \frac{ℓ_z}{r_z}=\frac{3.50 \times 1,000}{8.99 \times 10}=38.9$
    • よって、軸方向圧縮の計算式は、18<ℓ/r≦92 より（H11道仮p.47）
$$ \begin{equation} \begin{split} \sigma_{caz}&=[140-0.82(ℓ/r_z-18)]\times 1.5\\[5px] &=[140-0.82(38.9-18)]\times1.5\\[5px] &=184.3\ \mathrm{N/mm^2} \end{split}\nonumber \end{equation} $$
  • $\sigma_{bagy}$：局部座屈を考慮しない強軸まわりの許容曲げ圧縮応力度（N/mm²）
    • ただし、$2A_c \geqq A_w$
    • $A_c$：圧縮フランジの総断面積
      • $A_c=350 \times 19 = 6,650\ \mathrm{mm^2}$
    • $A_w$：ウェブの総断面積
      • $A_w=(350 - 2 \times 19) \times 12 = 3,744\ \mathrm{mm^2}$
    • $ℓ_y$：フランジ間の固定間距離（鉛直方向座屈長）
      • $ℓ_y=3.50\ \mathrm{m}$（H11道仮p.122）
    • よって、$ℓ/b$は、
      • $\displaystyle \frac{ℓ_y}{b}=\frac{3.50 \times 1,000}{350}=10.0$
    • よって、曲げ圧縮縁の計算式は、4.5 <$ℓ/b$≦30より(H11道仮p47)
$$ \begin{equation} \begin{split} \sigma_{bagy}&=\{140 - 2.4 ( ℓ_y / b - 4.5)\} \times 1.5\\[5px] &=\{140 - 2.4 ( 10.0 - 4.5)\} \times 1.5\\[5px] &=190.2 \ \mathrm{N/mm^2} \end{split} \nonumber \end{equation} $$
  • $\sigma_{ba0}$：局部座屈を考慮しない許容曲げ圧縮応力度の上限値
    • $\sigma_{ba0}=210 \ \mathrm{N/mm^2}$（H11道仮p51）
  • $\sigma_{caℓ}$：圧縮応力を受ける自由突出板の局部座屈に対する許容応力度
    • $\sigma_{caℓ}=210 \ \mathrm{N/mm^2}$（H11道仮p51）
    • ただし、$b ^\prime \leqq 13.1\ t ^\prime$とする。
  • $\sigma_{eay}$, $\sigma_{eaz}$：それぞれ強軸および弱軸まわりのオイラー座屈応力度（N/mm²） (H11道仮p51)
    • $\displaystyle \sigma_{eay}=\frac{1,200,000}{(ℓ ^\prime / r_y)^2}=\frac{1,200,000}{(3,500/151.0)^2}=\frac{1,200,000}{537.3}=2,233.6\ \mathrm{N/mm^2}$
    • $\displaystyle \sigma_{eaz}=\frac{1,200,000}{(ℓ ^\prime / r_z)^2}=\frac{1,200,000}{(3,500/89.9)^2}=\frac{1,200,000}{1,515.7}=791.7\ \mathrm{N/mm^2}$
      • $ℓ ^\prime$：材料両端の支点条件より定まる有効座屈長（mm）
      • $ℓ ^\prime=3.50 \times 1,000 = 3,500\ \mathrm{mm}$
      • $r_y, r_z$：それぞれ強軸および弱軸まわりの断面二次半径（mm）
      • $r_y=15.10 \times 10 = 151.0\ \mathrm{mm}$
      • $r_z=8.99 \times 10 = 89.9\ \mathrm{mm}$

よって、
照査式(2-6-1)

$$ \begin{equation} \begin{split} \frac{\sigma_c}{\sigma_{caz}}&+\frac{\sigma_{bcy}}{\sigma_{bagy}(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{\sigma_{bao}(1-\frac{\sigma_c}{\sigma_{eaz}})}\\[5px] &= \frac{45.3}{184.3}+\frac{120.8}{190.2(1-\frac{45.3}{2,233.6})}+\frac{0.0}{210.0(1-\frac{45.3}{791.7})} \\[5px] &=0.25+0.65+0.00\\[5px] &=0.90\leqq 1 \ \ \mathrm{OK} \end{split} \nonumber \end{equation} $$

照査式（2-6-2）

$$ \begin{equation} \begin{split} \sigma_c&+\frac{\sigma_{bcy}}{(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{(1-\frac{\sigma_c}{\sigma_{eaz}})} \\[5px] &=45.3+\frac{120.8}{(1-\frac{45.3}{2,233.6})}+\frac{0.0}{(1-\frac{45.3}{791.7})} \\[5px] &=45.3+123.3+0.0 \\[5px] &=168.7 \leqq \sigma_{caℓ}＝210.0 \ \ \mathrm{OK} \end{split} \nonumber \end{equation} $$
(2) せん断力の照査

最大せん断力をウェブの面積で除して求める。

$$ \begin{equation} \begin{split} \tau &= \frac{S_{max2}}{A_w} \\[5px] &= \frac{276.14 \times 1,000}{(350 - 2 \times 19)\times 12} \\[5px] &= 73.8 \leqq \tau_a＝120.0 \ \ \mathrm{OK} \end{split} \nonumber \end{equation} $$

5-2. 端部

5-2-1. 荷重の計算

一般部の計算より、

上段の「単位長さあたりの支保工反力」は

$$ R_1=121.65 \ \mathrm{kN/m} $$

下段の「単位長さあたりの支保工反力」は

$$ R_2=157.80 \ \mathrm{kN/m} $$

5-2-2. 断面力の計算

(1) 諸条件の計算

端部においては、掘削幅（短辺）から火打ちを差し引いた長さを支間（スパン）とする単純ばりとして断面力を計算する。（H11道仮p118,119）

掘削幅（短辺） $B_e=7.20 \ \mathrm{m}$
火打ちの腹起し方向の幅 $ℓ_2'=2.00 \ \mathrm{m}$
火打ち間の幅 $ℓ_1' = B_e - 2 \cdot ℓ_2'$ $= 7.20 - 2 \times 2.00$ $= 3.20\ \mathrm{m}$
火打ちの角度 $\theta =45 \ \mathrm{度}$
よって、H11道仮p118より、支間は
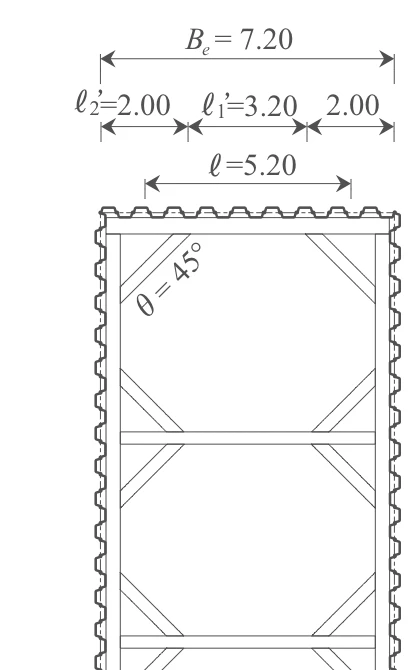
$$ \begin{equation} \begin{split} ℓ' &= ℓ_1' + ℓ_2' \\[5px] &= 3.20 + 2.00 \\[5px] &= 5.20\ \mathrm{m} \end{split}\nonumber \end{equation} $$

端部は、軸力が作用する腹起し材であるため、曲げと圧縮を受ける部材として設計する。

火打ちの腹起し方向の幅（端部）
$$ ℓ_4'=2.00 \ \mathrm{m} $$

火打ち間の幅（端部）

$$ \begin{equation} \begin{split} ℓ_3' &= B - ℓ_2 - ℓ_4' \\[5px] &= 5.00 - 1.50 - 2.00 \\[5px] &= 1.50\ \mathrm{m} \end{split}\nonumber \end{equation} $$
よって、軸力を考慮する腹起しの軸力分担幅は、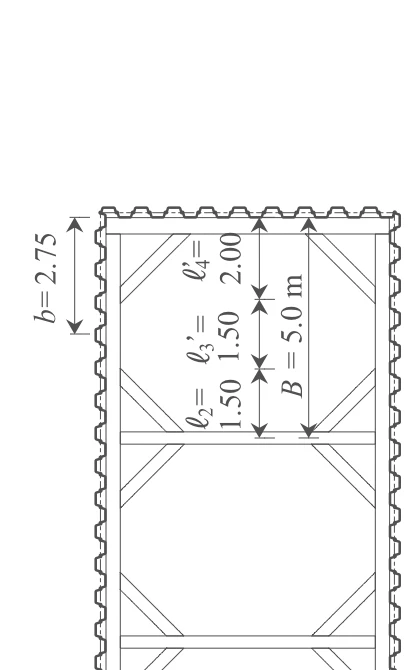
$$ \begin{equation} \begin{split} b &= \frac{1}{2} \cdot ℓ_3' + ℓ_4' \\[5px] &= \frac{1}{2} \times 1.50 + 2.00 \\[5px] &= 2.75\ \mathrm{m} \end{split}\nonumber \end{equation} $$

温度変化に伴う軸力増加は$\Delta N = 150 \ \mathrm{kN}$とする。

(2) 上段

＜軸力＞

$$ \begin{equation} \begin{split} N_1 &= (R_1 \cdot b + \Delta N) / 本数 \\[5px] &= (121.65 \times 2.75 + 150) /1 \\[5px] &= 484.53\ \mathrm{kN} \end{split}\nonumber \end{equation} $$

＜最大曲げモーメント＞

$$ \begin{equation} \begin{split} M_{max1} &= \frac{R_1 \cdot ℓ'^2}{8} \times \frac{1}{本数} \\[5px] &= \frac{121.65 \times 5.20^2}{8} \times \frac{1}{1} \\[5px] &= 411.16\ \mathrm{kN・m} \end{split}\nonumber \end{equation} $$

＜最大せん断力＞

$$ \begin{equation} \begin{split} S_{max1} &= \frac{R_1 \cdot ℓ'}{2} \times \frac{1}{本数} \\[5px] &= \frac{121.65 \times 5.20}{2} \times \frac{1}{1} \\[5px] &= 316.28\ \mathrm{kN・m} \end{split}\nonumber \end{equation} $$
(3) 下段

＜軸力＞

$$ \begin{equation} \begin{split} N_2 &= (R_2 \cdot b + \Delta N) / 本数 \\[5px] &= (157.80 \times 2.75 + 150) /2 \\[5px] &= 291.97\ \mathrm{kN} \end{split}\nonumber \end{equation} $$

＜最大曲げモーメント＞

$$ \begin{equation} \begin{split} M_{max2} &= \frac{R_2 \cdot ℓ^2}{8} \times \frac{1}{本数} \\[5px] &= \frac{157.80 \times 5.20^2}{8} \times \frac{1}{2} \\[5px] &= 266.68\ \mathrm{kN・m} \end{split}\nonumber \end{equation} $$

＜最大せん断力＞

$$ \begin{equation} \begin{split} S_{max2} &= \frac{R_2 \cdot ℓ}{2} \times \frac{1}{本数} \\[5px] &= \frac{157.80 \times 5.20}{2} \times \frac{1}{2} \\[5px] &= 205.14\ \mathrm{kN・m} \end{split}\nonumber \end{equation} $$

5-2-3. 応力度の照査（上段）

(1) 安定の照査

照査は、２つの照査式で行う。（H11道仮p50）

照査式（2-6-1）

$$ \begin{equation} \begin{split} \frac{\sigma_c}{\sigma_{caz}}+\frac{\sigma_{bcy}}{\sigma_{bagy}(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{\sigma_{bao}(1-\frac{\sigma_c}{\sigma_{eaz}})} \leqq 1 \end{split} \nonumber \end{equation} $$

照査式（2-6-2）

$$ \sigma_c+\frac{\sigma_{bcy}}{(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{(1-\frac{\sigma_c}{\sigma_{eaz}})} \leqq \sigma_{caℓ} \nonumber $$

ここに、

  • $\sigma_c$：照査する断面に作用する軸方向力による圧縮応力度（N/mm²）
    • $\displaystyle \sigma_c=\frac{N}{A}=\frac{484.5 \times 1,000}{197.70 \times 100}=24.5\ \mathrm{N/mm^2}$
  • $\sigma_{bcy}$：強軸まわりに作用する曲げモーメントによる曲げ圧縮応力度（N/mm²）
    • $\displaystyle \sigma_{bcy}=\frac{M_{max}}{Z}=\frac{411.2 \times 1,000,000}{2,950 \times 1,000}=139.4\ \mathrm{N/mm^2}$
  • $\sigma_{bcz}$：弱軸まわりに作用する曲げモーメントによる曲げ圧縮応力度（N/mm²）
    • $\displaystyle \sigma_{bcz}=0$
  • $\sigma_{caz}$：弱軸まわりの許容軸方向圧縮応力度（N/mm²）
    • ただし、$b ^\prime \leqq 13.1\ t ^\prime$ とする
    • $b ^\prime$：切ばりのフランジ片幅
      • $b ^\prime = ( 400-13)/2=194 \ \mathrm{mm}$
    • $t ^\prime$：切ばりのフランジ厚
      • $t ^\prime = 21 \ \mathrm{mm}$
    • $ℓ_z$：切ばりの弱軸まわりの座屈長（水平方向座屈長）
      • $ℓ_z=5.20 \ \mathrm{m}$（H11道仮p122より）
    • よって、弱軸の細長比は、
      • $\displaystyle \frac{ℓ_z}{r_z}=\frac{5.20 \times 1,000}{10.10 \times 10}=51.5$
    • よって、軸方向圧縮の計算式は、18<ℓ/r≦92 より（H11道仮p.47）
$$ \begin{equation} \begin{split} \sigma_{caz}&=[140-0.82(ℓ/r_z-18)]\times 1.5\\[5px] &=[140-0.82(51.5-18)]\times1.5\\[5px] &=168.8\ \mathrm{N/mm^2} \end{split}\nonumber \end{equation} $$
  • $\sigma_{bagy}$：局部座屈を考慮しない強軸まわりの許容曲げ圧縮応力度（N/mm²）
    • ただし、$2A_c \geqq A_w$
    • $A_c$：圧縮フランジの総断面積
      • $A_c=400 \times 21 = 8,400\ \mathrm{mm^2}$
    • $A_w$：ウェブの総断面積
      • $A_w=(400 - 2 \times 21) \times 13 = 4,654\ \mathrm{mm^2}$
    • $ℓ_y$：フランジ間の固定間距離（鉛直方向座屈長）
      • $ℓ_y=5.20\ \mathrm{m}$（H11道仮p.122）
    • よって、$ℓ/b$は、
      • $\displaystyle \frac{ℓ_y}{b}=\frac{5.20 \times 1,000}{400}=13.0$
    • よって、曲げ圧縮縁の計算式は、4.5 <$ℓ/b$≦30より(H11道仮p47)
$$ \begin{equation} \begin{split} \sigma_{bagy}&=\{140 - 2.4 ( ℓ_y / b - 4.5)\} \times 1.5\\[5px] &=\{140 - 2.4 ( 13.0 - 4.5)\} \times 1.5\\[5px] &=179.4 \ \mathrm{N/mm^2} \end{split} \nonumber \end{equation} $$
  • $\sigma_{ba0}$：局部座屈を考慮しない許容曲げ圧縮応力度の上限値
    • $\sigma_{ba0}=210 \ \mathrm{N/mm^2}$（H11道仮p51）
  • $\sigma_{caℓ}$：圧縮応力を受ける自由突出板の局部座屈に対する許容応力度
    • $\sigma_{caℓ}=210 \ \mathrm{N/mm^2}$（H11道仮p51）
    • ただし、$b ^\prime \leqq 13.1\ t ^\prime$とする。
  • $\sigma_{eay}$, $\sigma_{eaz}$：それぞれ強軸および弱軸まわりのオイラー座屈応力度（N/mm²） (H11道仮p51)
    • $\displaystyle \sigma_{eay}=\frac{1,200,000}{(ℓ ^\prime / r_y)^2}=\frac{1,200,000}{(5,200/173.0)^2}=\frac{1,200,000}{903.5}=1,328.2\ \mathrm{N/mm^2}$
    • $\displaystyle \sigma_{eaz}=\frac{1,200,000}{(ℓ ^\prime / r_z)^2}=\frac{1,200,000}{(5,200/101.0)^2}=\frac{1,200,000}{2,650.7}=452.7\ \mathrm{N/mm^2}$
      • $ℓ ^\prime$：材料両端の支点条件より定まる有効座屈長（mm）
      • $ℓ ^\prime=5.20 \times 1,000 = 5,200\ \mathrm{mm}$
      • $r_y, r_z$：それぞれ強軸および弱軸まわりの断面二次半径（mm）
      • $r_y=17.30 \times 10 = 173.0\ \mathrm{mm}$
      • $r_z=10.10 \times 10 = 101.0\ \mathrm{mm}$

よって、
照査式(2-6-1)

$$ \begin{equation} \begin{split} \frac{\sigma_c}{\sigma_{caz}}&+\frac{\sigma_{bcy}}{\sigma_{bagy}(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{\sigma_{bao}(1-\frac{\sigma_c}{\sigma_{eaz}})}\\[5px] &= \frac{24.5}{168.8}+\frac{139.4}{179.4(1-\frac{24.5}{1,328.2})}+\frac{0.0}{210.0(1-\frac{24.5}{452.7})} \\[5px] &=0.15+0.79+0.00\\[5px] &=0.94\leqq 1 \ \ \mathrm{OK} \end{split} \nonumber \end{equation} $$

照査式（2-6-2）

$$ \begin{equation} \begin{split} \sigma_c&+\frac{\sigma_{bcy}}{(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{(1-\frac{\sigma_c}{\sigma_{eaz}})} \\[5px] &=24.5+\frac{139.4}{(1-\frac{24.5}{1,328.2})}+\frac{0.0}{(1-\frac{24.5}{452.7})} \\[5px] &=24.5+142.0+0.0 \\[5px] &=166.5 \leqq \sigma_{caℓ}＝210.0 \ \ \mathrm{OK} \end{split} \nonumber \end{equation} $$
(2) せん断力の照査

最大せん断力をウェブの面積で除して求める。

$$ \begin{equation} \begin{split} \tau &= \frac{S_{max1}}{A_w} \\[5px] &= \frac{316.28 \times 1,000}{(400 - 2 \times 21)\times 13} \\[5px] &= 68.0 \leqq \tau_a＝120.0 \ \ \mathrm{OK} \end{split} \nonumber \end{equation} $$

5-2-4. 応力度の照査（下段）

(1) 安定の照査

照査は、２つの照査式で行う。（H11道仮p50）

照査式（2-6-1）

$$ \begin{equation} \begin{split} \frac{\sigma_c}{\sigma_{caz}}+\frac{\sigma_{bcy}}{\sigma_{bagy}(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{\sigma_{bao}(1-\frac{\sigma_c}{\sigma_{eaz}})} \leqq 1 \end{split} \nonumber \end{equation} $$

照査式（2-6-2）

$$ \sigma_c+\frac{\sigma_{bcy}}{(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{(1-\frac{\sigma_c}{\sigma_{eaz}})} \leqq \sigma_{caℓ} \nonumber $$

ここに、

  • $\sigma_c$：照査する断面に作用する軸方向力による圧縮応力度（N/mm²）
    • $\displaystyle \sigma_c=\frac{N}{A}=\frac{292.0 \times 1,000}{154.90 \times 100}=18.8\ \mathrm{N/mm^2}$
  • $\sigma_{bcy}$：強軸まわりに作用する曲げモーメントによる曲げ圧縮応力度（N/mm²）
    • $\displaystyle \sigma_{bcy}=\frac{M_{max}}{Z}=\frac{266.7 \times 1,000,000}{2,000 \times 1,000}=133.3\ \mathrm{N/mm^2}$
  • $\sigma_{bcz}$：弱軸まわりに作用する曲げモーメントによる曲げ圧縮応力度（N/mm²）
    • $\displaystyle \sigma_{bcz}=0$
  • $\sigma_{caz}$：弱軸まわりの許容軸方向圧縮応力度（N/mm²）
    • ただし、$b ^\prime \leqq 13.1\ t ^\prime$ とする
    • $b ^\prime$：切ばりのフランジ片幅
      • $b ^\prime = ( 350-12)/2=169 \ \mathrm{mm}$
    • $t ^\prime$：切ばりのフランジ厚
      • $t ^\prime = 19 \ \mathrm{mm}$
    • $ℓ_z$：切ばりの弱軸まわりの座屈長（水平方向座屈長）
      • $ℓ_z=5.20 \ \mathrm{m}$（H11道仮p122より）
    • よって、弱軸の細長比は、
      • $\displaystyle \frac{ℓ_z}{r_z}=\frac{5.20 \times 1,000}{8.99 \times 10}=57.8$
    • よって、軸方向圧縮の計算式は、18<ℓ/r≦92 より（H11道仮p.47）
$$ \begin{equation} \begin{split} \sigma_{caz}&=[140-0.82(ℓ/r_z-18)]\times 1.5\\[5px] &=[140-0.82(57.8-18)]\times1.5\\[5px] &=161.0\ \mathrm{N/mm^2} \end{split}\nonumber \end{equation} $$
  • $\sigma_{bagy}$：局部座屈を考慮しない強軸まわりの許容曲げ圧縮応力度（N/mm²）
    • ただし、$2A_c \geqq A_w$
    • $A_c$：圧縮フランジの総断面積
      • $A_c=350 \times 19 = 6,650\ \mathrm{mm^2}$
    • $A_w$：ウェブの総断面積
      • $A_w=(350 - 2 \times 19) \times 12 = 3,744\ \mathrm{mm^2}$
    • $ℓ_y$：フランジ間の固定間距離（鉛直方向座屈長）
      • $ℓ_y=5.20\ \mathrm{m}$（H11道仮p.122）
    • よって、$ℓ/b$は、
      • $\displaystyle \frac{ℓ_y}{b}=\frac{5.20 \times 1,000}{350}=14.9$
    • よって、曲げ圧縮縁の計算式は、4.5 <$ℓ/b$≦30より(H11道仮p47)
$$ \begin{equation} \begin{split} \sigma_{bagy}&=\{140 - 2.4 ( ℓ_y / b - 4.5)\} \times 1.5\\[5px] &=\{140 - 2.4 ( 14.9 - 4.5)\} \times 1.5\\[5px] &=172.7 \ \mathrm{N/mm^2} \end{split} \nonumber \end{equation} $$
  • $\sigma_{ba0}$：局部座屈を考慮しない許容曲げ圧縮応力度の上限値
    • $\sigma_{ba0}=210 \ \mathrm{N/mm^2}$（H11道仮p51）
  • $\sigma_{caℓ}$：圧縮応力を受ける自由突出板の局部座屈に対する許容応力度
    • $\sigma_{caℓ}=210 \ \mathrm{N/mm^2}$（H11道仮p51）
    • ただし、$b ^\prime \leqq 13.1\ t ^\prime$とする。
  • $\sigma_{eay}$, $\sigma_{eaz}$：それぞれ強軸および弱軸まわりのオイラー座屈応力度（N/mm²） (H11道仮p51)
    • $\displaystyle \sigma_{eay}=\frac{1,200,000}{(ℓ ^\prime / r_y)^2}=\frac{1,200,000}{(5,200/151.0)^2}=\frac{1,200,000}{1,185.9}=1,011.9\ \mathrm{N/mm^2}$
    • $\displaystyle \sigma_{eaz}=\frac{1,200,000}{(ℓ ^\prime / r_z)^2}=\frac{1,200,000}{(5,200/89.9)^2}=\frac{1,200,000}{3,345.7}=358.7\ \mathrm{N/mm^2}$
      • $ℓ ^\prime$：材料両端の支点条件より定まる有効座屈長（mm）
      • $ℓ ^\prime=5.20 \times 1,000 = 5,200\ \mathrm{mm}$
      • $r_y, r_z$：それぞれ強軸および弱軸まわりの断面二次半径（mm）
      • $r_y=15.10 \times 10 = 151.0\ \mathrm{mm}$
      • $r_z=8.99 \times 10 = 89.9\ \mathrm{mm}$

よって、
照査式(2-6-1)

$$ \begin{equation} \begin{split} \frac{\sigma_c}{\sigma_{caz}}&+\frac{\sigma_{bcy}}{\sigma_{bagy}(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{\sigma_{bao}(1-\frac{\sigma_c}{\sigma_{eaz}})}\\[5px] &= \frac{18.8}{161.0}+\frac{133.3}{172.7(1-\frac{18.8}{1,011.9})}+\frac{0.0}{210.0(1-\frac{18.8}{358.7})} \\[5px] &=0.12+0.79+0.00\\[5px] &=0.91\leqq 1 \ \ \mathrm{OK} \end{split} \nonumber \end{equation} $$

照査式（2-6-2）

$$ \begin{equation} \begin{split} \sigma_c&+\frac{\sigma_{bcy}}{(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{(1-\frac{\sigma_c}{\sigma_{eaz}})} \\[5px] &=18.8+\frac{133.3}{(1-\frac{18.8}{1,011.9})}+\frac{0.0}{(1-\frac{18.8}{358.7})} \\[5px] &=18.8+135.9+0.0 \\[5px] &=154.7 \leqq \sigma_{caℓ}＝210.0 \ \ \mathrm{OK} \end{split} \nonumber \end{equation} $$
(2) せん断力の照査

最大せん断力をウェブの面積で除して求める。

$$ \begin{equation} \begin{split} \tau &= \frac{S_{max2}}{A_w} \\[5px] &= \frac{205.14 \times 1,000}{(350 - 2 \times 19)\times 12} \\[5px] &= 54.8 \leqq \tau_a＝120.0 \ \ \mathrm{OK} \end{split} \nonumber \end{equation} $$

6. 切ばりの設計

6-1. 荷重の計算

荷重は、腹起しの設計で算出した「単位長さあたりの支保工反力」なので、

  • 上段　$w_{x1}=121.65 \ \mathrm{kN/m}$
  • 下段　$w_{x2}=157.80 \ \mathrm{kN/m}$

曲げモーメントは、鉛直方向座屈長（中間杭がないため、切ばり全長）をスパンとする単純ばりで計算する。

曲げ荷重$w$は、切ばりの自重を含めて、下記のとおりとする。（H11道仮p122）

  • $w=5.00 \ \mathrm{kN/m}$

軸力は、「土圧」、「水圧」、および「温度変化に伴う軸力」を考慮する。

温度変化に伴う軸力増加は$\Delta N = 150 \ \mathrm{kN}$とする。

6-2. 断面力の計算

切ばりは、「軸力」と「モーメント」が作用する部材として設計する。

  • 軸力を考慮する荷重負担幅（水平間隔） $ℓ_1 = ℓ_2 = 5.00 \ \mathrm{m}$
  • 鉛直方向の座屈長（切ばり全長） $L_1 = 6.30 \ \mathrm{m}$
  • 水平方向の座屈長（火打ち間距離） $L_2 = 6.30- (1.50 \times \tan(45)) \times 2$ $= 3.33 \ \mathrm{m}$

(1) 上段

＜軸力＞

$$ \begin{equation} \begin{split} N_1 &= w_{x1} \cdot \frac{ℓ_1 + ℓ_2}{2} + \Delta N \\[5px] &= 121.65 \times \frac{5.00 + 5.00}{2} + 150 \\[5px] &= 758.2\ \mathrm{kN} \end{split}\nonumber \end{equation} $$

＜最大曲げモーメント＞

$$ \begin{equation} \begin{split} M_{max1} &= \frac{w \cdot L_1^2}{8} \\[5px] &= \frac{5.00 \times 6.30^2}{8} \\[5px] &= 24.8\ \mathrm{kN・m} \end{split}\nonumber \end{equation} $$

(2) 下段

＜軸力＞

$$ \begin{equation} \begin{split} N_2 &= w_{x2} \cdot \frac{ℓ_1 + ℓ_2}{2} + \Delta N \\[5px] &= 157.80 \times \frac{5.00 + 5.00}{2} + 150 \\[5px] &= 939.0\ \mathrm{kN} \end{split}\nonumber \end{equation} $$

＜最大曲げモーメント＞

$$ \begin{equation} \begin{split} M_{max2} &= \frac{w \cdot L_1^2}{8} \\[5px] &= \frac{5.00 \times 6.30^2}{8} \\[5px] &= 24.8\ \mathrm{kN・m} \end{split}\nonumber \end{equation} $$

6-3. 応力度の照査（上段）

照査は、安定の照査のみで、せん断力の照査は行わない。

２つの照査式で行う。（H11道仮p50）

照査式（2-6-1）

$$ \begin{equation} \begin{split} \frac{\sigma_c}{\sigma_{caz}}+\frac{\sigma_{bcy}}{\sigma_{bagy}(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{\sigma_{bao}(1-\frac{\sigma_c}{\sigma_{eaz}})} \leqq 1 \end{split} \nonumber \end{equation} $$

照査式（2-6-2）

$$ \sigma_c+\frac{\sigma_{bcy}}{(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{(1-\frac{\sigma_c}{\sigma_{eaz}})} \leqq \sigma_{caℓ} \nonumber $$

ここに、

  • $\sigma_c$：照査する断面に作用する軸方向力による圧縮応力度（N/mm²）
    • $\displaystyle \sigma_c=\frac{N}{A}=\frac{758.2 \times 1,000}{104.80 \times 100}=72.4\ \mathrm{N/mm^2}$
  • $\sigma_{bcy}$：強軸まわりに作用する曲げモーメントによる曲げ圧縮応力度（N/mm²）
    • $\displaystyle \sigma_{bcy}=\frac{M_{max}}{Z}=\frac{24.8 \times 1,000,000}{1,150 \times 1,000}=21.6\ \mathrm{N/mm^2}$
  • $\sigma_{bcz}$：弱軸まわりに作用する曲げモーメントによる曲げ圧縮応力度（N/mm²）
    • $\displaystyle \sigma_{bcz}=0$
  • $\sigma_{caz}$：弱軸まわりの許容軸方向圧縮応力度（N/mm²）
    • ただし、$b ^\prime \leqq 13.1\ t ^\prime$ とする
    • $b ^\prime$：切ばりのフランジ片幅
      • $b ^\prime = ( 300-10)/2=145 \ \mathrm{mm}$
    • $t ^\prime$：切ばりのフランジ厚
      • $t ^\prime = 15 \ \mathrm{mm}$
    • $ℓ_z$：切ばりの弱軸まわりの座屈長（水平方向座屈長）
      • $ℓ_z=3.30 \ \mathrm{m}$（H11道仮p122より）
    • よって、弱軸の細長比は、
      • $\displaystyle \frac{ℓ_z}{r_z}=\frac{3.30 \times 1,000}{7.51 \times 10}=43.9$
    • よって、軸方向圧縮の計算式は、18<ℓ/r≦92 より（H11道仮p.47）
$$ \begin{equation} \begin{split} \sigma_{caz}&=[140-0.82(ℓ/r_z-18)]\times 1.5\\[5px] &=[140-0.82(43.9-18)]\times1.5\\[5px] &=178.1\ \mathrm{N/mm^2} \end{split}\nonumber \end{equation} $$
  • $\sigma_{bagy}$：局部座屈を考慮しない強軸まわりの許容曲げ圧縮応力度（N/mm²）
    • ただし、$2A_c \geqq A_w$
    • $A_c$：圧縮フランジの総断面積
      • $A_c=300 \times 15 = 4,500\ \mathrm{mm^2}$
    • $A_w$：ウェブの総断面積
      • $A_w=(300 - 2 \times 15) \times 10 = 2,700\ \mathrm{mm^2}$
    • $ℓ_y$：フランジ間の固定間距離（鉛直方向座屈長）
      • $ℓ_y=6.30\ \mathrm{m}$（H11道仮p.122）
    • よって、$ℓ/b$は、
      • $\displaystyle \frac{ℓ_y}{b}=\frac{6.30 \times 1,000}{300}=21.0$
    • よって、曲げ圧縮縁の計算式は、4.5 <$ℓ/b$≦30より(H11道仮p47)
$$ \begin{equation} \begin{split} \sigma_{bagy}&=\{140 - 2.4 ( ℓ_y / b - 4.5)\} \times 1.5\\[5px] &=\{140 - 2.4 ( 21.0 - 4.5)\} \times 1.5\\[5px] &=150.6 \ \mathrm{N/mm^2} \end{split} \nonumber \end{equation} $$
  • $\sigma_{ba0}$：局部座屈を考慮しない許容曲げ圧縮応力度の上限値
    • $\sigma_{ba0}=210 \ \mathrm{N/mm^2}$（H11道仮p51）
  • $\sigma_{caℓ}$：圧縮応力を受ける自由突出板の局部座屈に対する許容応力度
    • $\sigma_{caℓ}=210 \ \mathrm{N/mm^2}$（H11道仮p51）
    • ただし、$b ^\prime \leqq 13.1\ t ^\prime$とする。
  • $\sigma_{eay}$, $\sigma_{eaz}$：それぞれ強軸および弱軸まわりのオイラー座屈応力度（N/mm²） (H11道仮p51)
    • $\displaystyle \sigma_{eay}=\frac{1,200,000}{(ℓ_1 ^\prime / r_y)^2}=\frac{1,200,000}{(6,300/129.0)^2}=\frac{1,200,000}{2,385.1}=503.1\ \mathrm{N/mm^2}$
    • $\displaystyle \sigma_{eaz}=\frac{1,200,000}{(ℓ_2 ^\prime / r_z)^2}=\frac{1,200,000}{(3,300/75.1)^2}=\frac{1,200,000}{1,930.8}=621.5\ \mathrm{N/mm^2}$
      • $ℓ ^\prime$：材料両端の支点条件より定まる有効座屈長（mm）
      • $ℓ_1 ^\prime=6.30 \times 1,000 = 6,300\ \mathrm{mm}$
      • $ℓ_2 ^\prime=3.30 \times 1,000 = 3,300\ \mathrm{mm}$
      • $r_y, r_z$：それぞれ強軸および弱軸まわりの断面二次半径（mm）
      • $r_y=12.90 \times 10 = 129.0\ \mathrm{mm}$
      • $r_z=7.51 \times 10 = 75.1\ \mathrm{mm}$

よって、
照査式(2-6-1)

$$ \begin{equation} \begin{split} \frac{\sigma_c}{\sigma_{caz}}&+\frac{\sigma_{bcy}}{\sigma_{bagy}(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{\sigma_{bao}(1-\frac{\sigma_c}{\sigma_{eaz}})}\\[5px] &= \frac{72.4}{178.1}+\frac{21.6}{150.6(1-\frac{72.4}{503.1})}+\frac{0.0}{210.0(1-\frac{72.4}{621.5})} \\[5px] &=0.41+0.17+0.00\\[5px] &=0.58\leqq 1 \ \ \mathrm{OK} \end{split} \nonumber \end{equation} $$

照査式（2-6-2）

$$ \begin{equation} \begin{split} \sigma_c&+\frac{\sigma_{bcy}}{(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{(1-\frac{\sigma_c}{\sigma_{eaz}})} \\[5px] &=72.4+\frac{21.6}{(1-\frac{72.4}{503.1})}+\frac{0.0}{(1-\frac{72.4}{621.5})} \\[5px] &=72.4+25.2+0.0 \\[5px] &=97.6 \leqq \sigma_{caℓ}＝210.0 \ \ \mathrm{OK} \end{split} \nonumber \end{equation} $$

6-4. 応力度の照査（下段）

照査は、安定の照査のみで、せん断力の照査は行わない。

２つの照査式で行う。（H11道仮p50）

照査式（2-6-1）

$$ \begin{equation} \begin{split} \frac{\sigma_c}{\sigma_{caz}}+\frac{\sigma_{bcy}}{\sigma_{bagy}(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{\sigma_{bao}(1-\frac{\sigma_c}{\sigma_{eaz}})} \leqq 1 \end{split} \nonumber \end{equation} $$

照査式（2-6-2）

$$ \sigma_c+\frac{\sigma_{bcy}}{(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{(1-\frac{\sigma_c}{\sigma_{eaz}})} \leqq \sigma_{caℓ} \nonumber $$

ここに、

  • $\sigma_c$：照査する断面に作用する軸方向力による圧縮応力度（N/mm²）
    • $\displaystyle \sigma_c=\frac{N}{A}=\frac{939.0 \times 1,000}{104.80 \times 100}=89.6\ \mathrm{N/mm^2}$
  • $\sigma_{bcy}$：強軸まわりに作用する曲げモーメントによる曲げ圧縮応力度（N/mm²）
    • $\displaystyle \sigma_{bcy}=\frac{M_{max}}{Z}=\frac{24.8 \times 1,000,000}{1,150 \times 1,000}=21.6\ \mathrm{N/mm^2}$
  • $\sigma_{bcz}$：弱軸まわりに作用する曲げモーメントによる曲げ圧縮応力度（N/mm²）
    • $\displaystyle \sigma_{bcz}=0$
  • $\sigma_{caz}$：弱軸まわりの許容軸方向圧縮応力度（N/mm²）
    • ただし、$b ^\prime \leqq 13.1\ t ^\prime$ とする
    • $b ^\prime$：切ばりのフランジ片幅
      • $b ^\prime = ( 300-10)/2=145 \ \mathrm{mm}$
    • $t ^\prime$：切ばりのフランジ厚
      • $t ^\prime = 15 \ \mathrm{mm}$
    • $ℓ_z$：切ばりの弱軸まわりの座屈長（水平方向座屈長）
      • $ℓ_z=3.30 \ \mathrm{m}$（H11道仮p122より）
    • よって、弱軸の細長比は、
      • $\displaystyle \frac{ℓ_z}{r_z}=\frac{3.30 \times 1,000}{7.51 \times 10}=43.9$
    • よって、軸方向圧縮の計算式は、18<ℓ/r≦92 より（H11道仮p.47）
$$ \begin{equation} \begin{split} \sigma_{caz}&=[140-0.82(ℓ/r_z-18)]\times 1.5\\[5px] &=[140-0.82(43.9-18)]\times1.5\\[5px] &=178.1\ \mathrm{N/mm^2} \end{split}\nonumber \end{equation} $$
  • $\sigma_{bagy}$：局部座屈を考慮しない強軸まわりの許容曲げ圧縮応力度（N/mm²）
    • ただし、$2A_c \geqq A_w$
    • $A_c$：圧縮フランジの総断面積
      • $A_c=300 \times 15 = 4,500\ \mathrm{mm^2}$
    • $A_w$：ウェブの総断面積
      • $A_w=(300 - 2 \times 15) \times 10 = 2,700\ \mathrm{mm^2}$
    • $ℓ_y$：フランジ間の固定間距離（鉛直方向座屈長）
      • $ℓ_y=6.30\ \mathrm{m}$（H11道仮p.122）
    • よって、$ℓ/b$は、
      • $\displaystyle \frac{ℓ_y}{b}=\frac{6.30 \times 1,000}{300}=21.0$
    • よって、曲げ圧縮縁の計算式は、4.5 <$ℓ/b$≦30より(H11道仮p47)
$$ \begin{equation} \begin{split} \sigma_{bagy}&=\{140 - 2.4 ( ℓ_y / b - 4.5)\} \times 1.5\\[5px] &=\{140 - 2.4 ( 21.0 - 4.5)\} \times 1.5\\[5px] &=150.6 \ \mathrm{N/mm^2} \end{split} \nonumber \end{equation} $$
  • $\sigma_{ba0}$：局部座屈を考慮しない許容曲げ圧縮応力度の上限値
    • $\sigma_{ba0}=210 \ \mathrm{N/mm^2}$（H11道仮p51）
  • $\sigma_{caℓ}$：圧縮応力を受ける自由突出板の局部座屈に対する許容応力度
    • $\sigma_{caℓ}=210 \ \mathrm{N/mm^2}$（H11道仮p51）
    • ただし、$b ^\prime \leqq 13.1\ t ^\prime$とする。
  • $\sigma_{eay}$, $\sigma_{eaz}$：それぞれ強軸および弱軸まわりのオイラー座屈応力度（N/mm²） (H11道仮p51)
    • $\displaystyle \sigma_{eay}=\frac{1,200,000}{(ℓ_1 ^\prime / r_y)^2}=\frac{1,200,000}{(6,300/129.0)^2}=\frac{1,200,000}{2,385.1}=503.1\ \mathrm{N/mm^2}$
    • $\displaystyle \sigma_{eaz}=\frac{1,200,000}{(ℓ_2 ^\prime / r_z)^2}=\frac{1,200,000}{(3,300/75.1)^2}=\frac{1,200,000}{1,930.8}=621.5\ \mathrm{N/mm^2}$
      • $ℓ ^\prime$：材料両端の支点条件より定まる有効座屈長（mm）
      • $ℓ_1 ^\prime=6.30 \times 1,000 = 6,300\ \mathrm{mm}$
      • $ℓ_2 ^\prime=3.30 \times 1,000 = 3,300\ \mathrm{mm}$
      • $r_y, r_z$：それぞれ強軸および弱軸まわりの断面二次半径（mm）
      • $r_y=12.90 \times 10 = 129.0\ \mathrm{mm}$
      • $r_z=7.51 \times 10 = 75.1\ \mathrm{mm}$

よって、
照査式(2-6-1)

$$ \begin{equation} \begin{split} \frac{\sigma_c}{\sigma_{caz}}&+\frac{\sigma_{bcy}}{\sigma_{bagy}(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{\sigma_{bao}(1-\frac{\sigma_c}{\sigma_{eaz}})}\\[5px] &= \frac{89.6}{178.1}+\frac{21.6}{150.6(1-\frac{89.6}{503.1})}+\frac{0.0}{210.0(1-\frac{89.6}{621.5})} \\[5px] &=0.50+0.17+0.00\\[5px] &=0.67\leqq 1 \ \ \mathrm{OK} \end{split} \nonumber \end{equation} $$

照査式（2-6-2）

$$ \begin{equation} \begin{split} \sigma_c&+\frac{\sigma_{bcy}}{(1-\frac{\sigma_c}{\sigma_{eay}})}+\frac{\sigma_{bcz}}{(1-\frac{\sigma_c}{\sigma_{eaz}})} \\[5px] &=89.6+\frac{21.6}{(1-\frac{89.6}{503.1})}+\frac{0.0}{(1-\frac{89.6}{621.5})} \\[5px] &=89.6+26.2+0.0 \\[5px] &=115.8 \leqq \sigma_{caℓ}＝210.0 \ \ \mathrm{OK} \end{split} \nonumber \end{equation} $$

7. 火打ちの設計

7-1. 荷重の計算

荷重は、腹起しの設計で算出した「単位長さあたりの支保工反力」なので、

  • 上段　$w_{x1}=121.65 \ \mathrm{kN/m}$
  • 下段　$w_{x2}=157.80 \ \mathrm{kN/m}$

曲げモーメントおよび自重は、スパンが短いため無視する。

軸力は、「土圧」、「水圧」、および「温度変化に伴う軸力」を考慮する。

温度変化に伴う軸力増加は$\Delta N = 150 \ \mathrm{kN}$とする。

7-2. 断面力の計算

切ばりの水平間隔 $B=5.00 \ \mathrm{m}$

火打ちの腹起し方向の幅 $ℓ_2=1.50 \ \mathrm{m}$

火打ち間の幅 $ℓ_1 = B - 2 \cdot ℓ_2$ $= 5.00 - 2 \times 1.50$ $= 2.00\ \mathrm{m}$

火打ちの角度 $\theta =45 \ \mathrm{度}$

(1) 上段

＜軸力＞

$$ \begin{equation} \begin{split} N_1 &= w_{x1} \cdot \frac{ℓ_1 + ℓ_2}{2} \cdot \frac{1}{\cos \theta} + \Delta N \\[5px] &= 121.65 \times \frac{2.00 + 1.50}{2} \times \frac{1}{0.71}+ 150 \\[5px] &= 451.1\ \mathrm{kN} \end{split}\nonumber \end{equation} $$

(2) 下段

＜軸力＞

$$ \begin{equation} \begin{split} N_2 &= w_{x2} \cdot \frac{ℓ_1 + ℓ_2}{2} \cdot \frac{1}{\cos \theta} + \Delta N \\[5px] &= 157.80 \times \frac{2.00 + 1.50}{2} \times \frac{1}{0.71}+ 150 \\[5px] &= 540.5\ \mathrm{kN} \end{split}\nonumber \end{equation} $$

7-3. 応力度の照査（上段）

  • $\sigma_c$：照査する断面に作用する軸方向力による圧縮応力度（N/mm²）
    • $\displaystyle \sigma_c=\frac{N}{A}=\frac{451.1 \times 1,000}{104.80 \times 100}=43.0\ \mathrm{N/mm^2}$
  • $\sigma_{ca}$：許容軸方向圧縮応力度（N/mm²）
    • $ℓ$：座屈長
      • $\displaystyle ℓ=\frac{ℓ_2}{\cos \theta} = \frac{1.50}{0.71}=2.12 \ \mathrm{m}$（H11道仮p122より）
    • よって、弱軸の細長比は、
      • $\displaystyle \frac{ℓ}{r_z}=\frac{2.12 \times 1,000}{7.51 \times 10}=28.2$
    • よって、軸方向圧縮の計算式は、18<ℓ/r≦92 より（H11道仮p.47）
$$ \begin{equation} \begin{split} \sigma_{ca}&=[140-0.82(ℓ/r_z-18)]\times 1.5\\[5px] &=[140-0.82(28.2-18)]\times1.5\\[5px] &=197.4\ \mathrm{N/mm^2} \end{split}\nonumber \end{equation} $$

よって、

$$ \sigma_c =43.0 \leqq \sigma_{caℓ}＝197.4 \ \ \mathrm{OK} $$

7-4. 応力度の照査（下段）

  • $\sigma_c$：照査する断面に作用する軸方向力による圧縮応力度（N/mm²）
    • $\displaystyle \sigma_c=\frac{N}{A}=\frac{540.5 \times 1,000}{104.80 \times 100}=51.6\ \mathrm{N/mm^2}$
  • $\sigma_{ca}$：許容軸方向圧縮応力度（N/mm²）
    • $ℓ$：座屈長
      • $\displaystyle ℓ=\frac{ℓ_2}{\cos \theta} = \frac{1.50}{0.71}=2.12 \ \mathrm{m}$（H11道仮p122より）
    • よって、弱軸の細長比は、
      • $\displaystyle \frac{ℓ}{r_z}=\frac{2.12 \times 1,000}{7.51 \times 10}=28.2$
    • よって、軸方向圧縮の計算式は、18<ℓ/r≦92 より（H11道仮p.47）
$$ \begin{equation} \begin{split} \sigma_{ca}&=[140-0.82(ℓ/r_z-18)]\times 1.5\\[5px] &=[140-0.82(28.2-18)]\times1.5\\[5px] &=197.4\ \mathrm{N/mm^2} \end{split}\nonumber \end{equation} $$

よって、

$$\sigma_c =51.6 \leqq \sigma_{caℓ}＝197.4 \ \ \mathrm{OK} $$

エクセルブック

計算を記載したエクセルブックは下記からダウンロードしてください。

DOWNLOAD

シートに保護をかけていますが、パスワードは設定していません。

分かりにくかったり、間違いを見つけられた場合は、ご連絡いただけると幸いです。