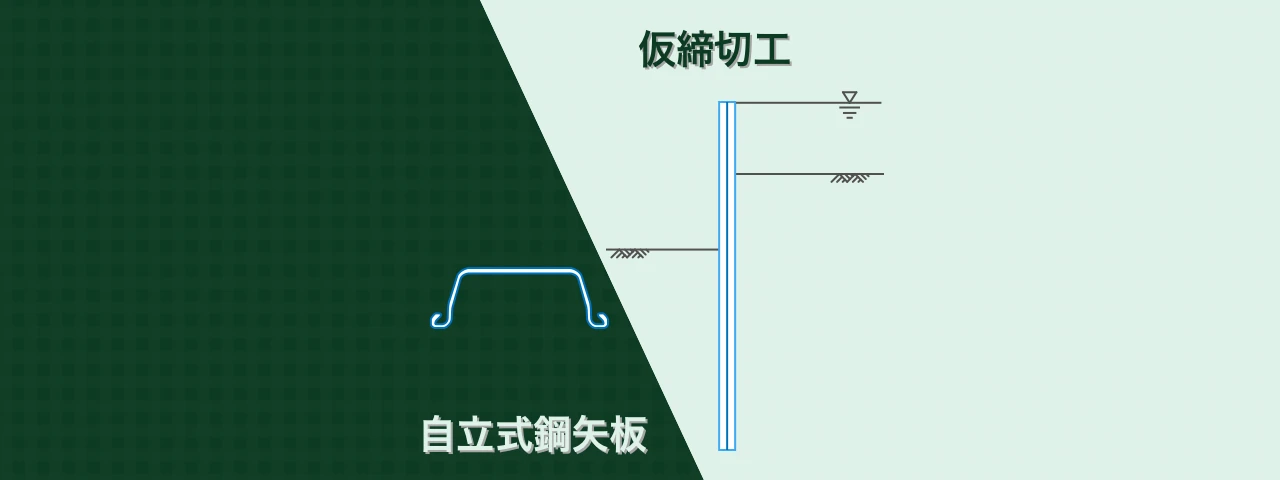
Excelで仮設土留め壁の設計計算 -自立式親杭横矢板、砂質地盤-

土木工事に用いられる仮設土留め壁「自立式親杭矢板」をエクセルで設計計算した結果をご紹介します。

設計の考え方とフローチャート

設計の考え方は、社団法人日本道路協会が平成11年3月に発行した道路土工仮設構造物工指針（以下、H11道仮という。）のp150～155に基づいています。

今回の紹介する設計プロセスは「掘削深さH=3.0m以下、砂質地盤の陸上施工」が適用範囲です。（H11道仮p28）

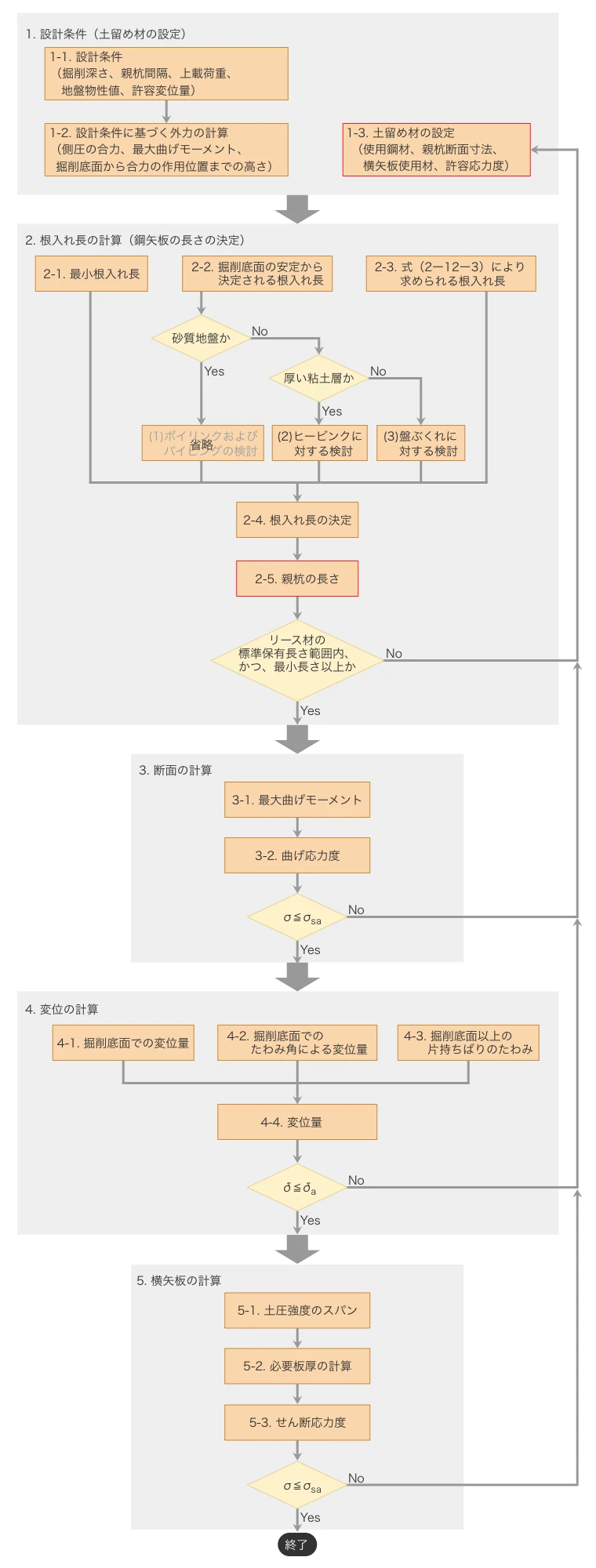
下記の画像は、設計のフローチャートです。クリックすると別ウィンドウで開きます。

1 設計条件

1-1 設計条件の設定

(1)掘削寸法・荷重・地下水位

• 掘削深さ $H=3.0\ \mathrm{m}$
• 親杭間隔 $a=1.5\ \mathrm{m}$
• 上載荷重 $q=10.0\ \mathrm{kN/m^2}$

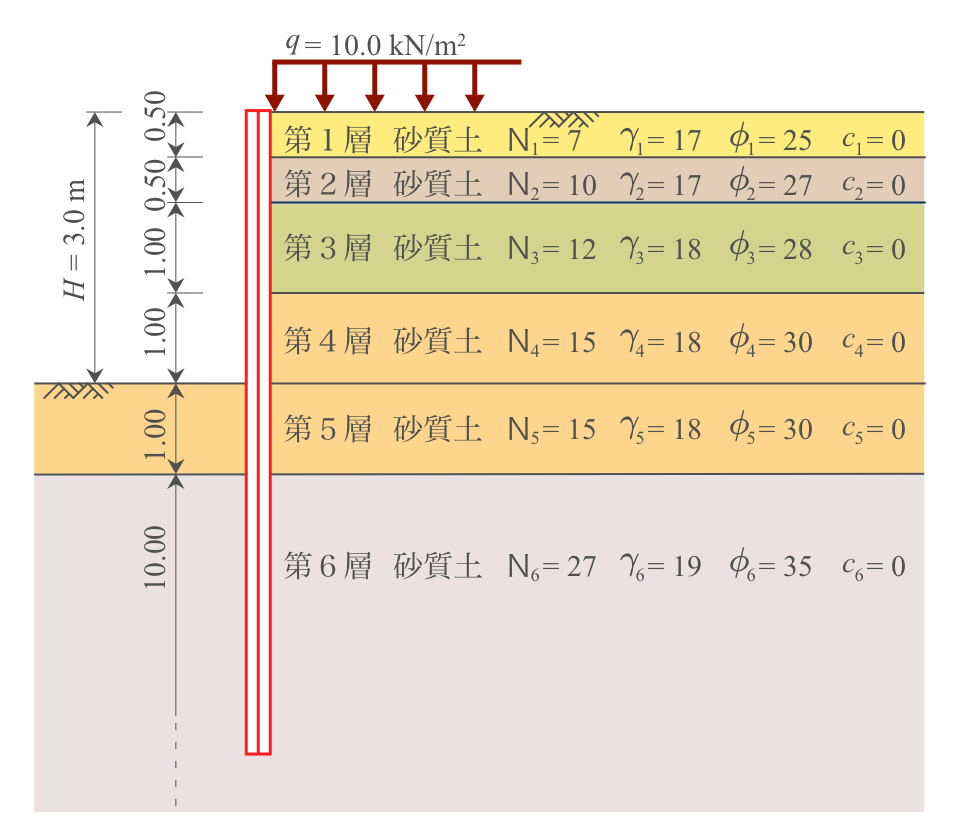
地盤物性値

地盤の各数値は上図のとおりですが、表にすると下記のとおりです。

	層厚 $h$ (m)	土質	水 (m)	N値	単位体積重量 $\gamma$ (kN/m3)	水中単位重量 $\gamma\ ^\prime$ (kN/m3)	せん断抵抗角 $\phi$ (度)	粘着力 $c$ (kN/m2)
1層	0.50	砂質土	なし	7	17	8	25	0
2層	0.50	砂質土	なし	10	17	8	27	0
3層	1.00	砂質土	なし	12	18	9	30	0
4層	1.00	砂質土	なし	15	18	9	30	0
掘削 $\sum$	3.00
5層	1.00	砂質土	なし	15	18	9	30	0
6層	10.00	砂質土	なし	27	19	10	35	0

📌NOTE
上記の表のうち、実際に計測するのは左の４つ「層厚」、「土質」、「水」、「N値」でしょう。 土の単位体積重量$\gamma$は、H11道仮p.29より選定し、水中単位体積重量も同ページのとおり、9.0kN/m3を差し引いて求めています。 せん断抵抗角はN値からの換算式$\phi=\sqrt{15N}+15$で求めることができます。（H11道仮p.30） 砂質土の粘着力は無視しています。（H11道仮p.30）

(2)土留め壁頭部の許容変位量

土留め壁頭部の許容変位量は、掘削深さの「3%」とします。（H11道仮p.151）

よって、許容変位量$\delta_a =3.0\times0.03=\textcolor{red}{0.090}\ \mathrm{m}$

1-2. 設計条件に基づく外力の計算

(1)掘削部の主働土圧

主働土圧は次の式で求めます。（H11道仮p.151）

$$ \begin{equation} \begin{split} p_a & =K_a\ \left(\sum\gamma\ h+q\right)-2c\sqrt{K_a}\\[5px] K_a & =\tan^2\left(45^\circ -\frac{\phi}{2}\right) \end{split}\nonumber \end{equation} $$

ここに、

• $p_a$：自立式土留めに作用する土圧（kN/m²）
• $K_a$：主働土圧係数
• $\sum \gamma\ h$：着目点における地盤の有効土かぶり圧（kN/m²）
• $\gamma$：各層の土の湿潤単位体積重量（kN/m³）
  • ただし、地下水位以下では水中単位体積重量$\gamma\ ^\prime$とする。
• $h$：着目点までの各層の層厚（m）
• $q$：地表面までの上載荷重（kN/m²）
• $c$：土の粘着力（kN/m²）
• $\phi$：土のせん断抵抗角（度）

以上をもとに、掘削部の各層の主働土圧を表計算すると次のとおり。

	層厚 $h$ (m)	土質	主働土圧係数 $K_a$	$\gamma$ (kN/m³)	主働土圧 $p_a$ (kN/m²)
1層	0.50	砂質	0.406	17	$p_{a1上}=4.06$ $p_{a1下}=7.51$
2層	0.50	砂質	0.376	17	$p_{a2上}=6.96$ $p_{a2下}=10.15$
3層	1.00	砂質	0.361	18	$p_{a3上}=9.75$ $p_{a3下}=16.25$
4層	1.00	砂質	0.333	18	$p_{a4上}=14.99$ $p_{a4下}=20.98$
	3.00

主働土圧に、作用幅「親杭間隔」を乗じて、親杭一本が分担する土圧強度を計算する。（H11道仮p.151）

		主働土圧 $p_a$ (kN/m²)	作用幅 $b$ (m)	土圧強度 $p$ (kN/m)
1層	上面 下面	$p_{a1上}=4.06$ $p_{a1下}=7.51$	1.5	$p_{1上}=6.09$ $p_{1下}=11.27$
2層	上面 下面	$p_{a2上}=6.96$ $p_{a2下}=10.15$	1.5	$p_{2上}=10.43$ $p_{2下}=15.23$
3層	上面 下面	$p_{a3上}=9.75$ $p_{a3下}=16.25$	1.5	$p_{3上}=14.62$ $p_{3下}=24.37$
4層	上面 下面	$p_{a4上}=14.99$ $p_{a4下}=20.98$	1.5	$p_{4上}=22.48$ $p_{4下}=31.47$

(2)側圧の合力

「側圧の合力」を求めるために、各層を２つに分割し各三角形の面積「側圧」を求め、それらを合計すれば「側圧の合力」となります。

		計算式	側圧 $P$ (kN)
1層	① ②	0.50×6.09 /2 0.50×11.27 /2	1.52 2.82
2層	③ ④	0.50×10.43 /2 0.50×15.23 /2	2,61 3.81
3層	⑤ ⑥	1.00×14.62 /2 1.00×24.37 /2	7.31 12.18
4層	⑦ ⑧	1.00×22.48 /2 1.00×31.47 /2	11.24 15.73
			57.22

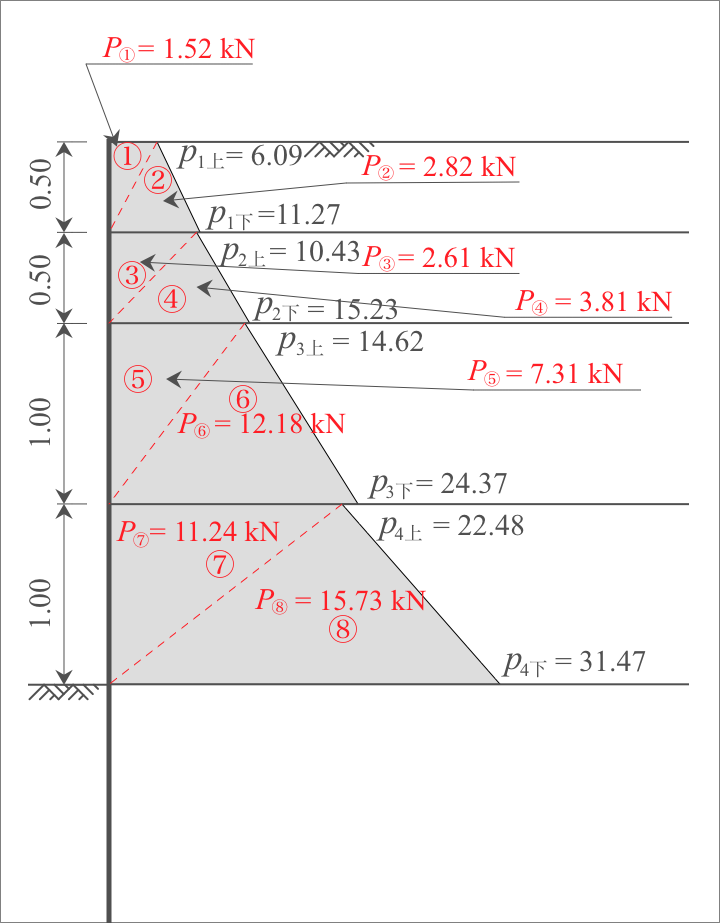
(3)最大曲げモーメント

つづいて、「最大曲げモーメント」を求めます。

まず、掘削底面から各三角形重心までの距離「アーム長」を算出します。下図の青字で示しています。

	計算式	アーム長 $y$ (m)
① ②	1.00+1.00+0.50+0.50 /3 ×2 1.00+1.00+0.50+0.50 /3	2.83 2.67
③ ④	1.00+1.00+0.50 /3 ×2 1.00+1.00+0.50 /3	2.33 2.17
⑤ ⑥	1.00+1.00 /3 ×2 1.00+1.00 /3	1.67 1.33
⑦ ⑧	1.00 /3 × 2 1.00 /3	0.67 0.33

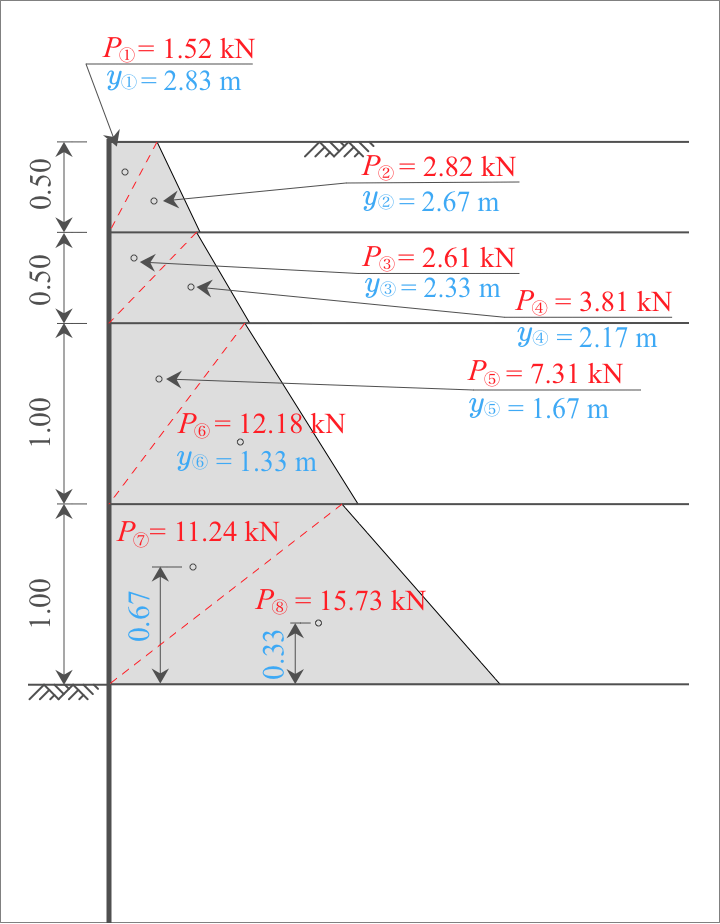
次に、各三角形の「側圧」に、それぞれの「アーム長」をかけ算して「モーメント」を求め、それらを合計すれば「最大曲げモーメント」となります。

	側圧 $P$ (kN)	アーム長 $y$ (m)	モーメント $M=P \cdot y$ (kN・m)
① ②	1.52 2.82	2.83 2.67	4.31 7.51
③ ④	2.61 3.81	2.33 2.17	6.09 8.25
⑤ ⑥	7.31 12.18	1.67 1.33	12.18 16.25
⑦ ⑧	11.24 15.73	0.67 0.33	7.49 5.24
	57.22		67.33

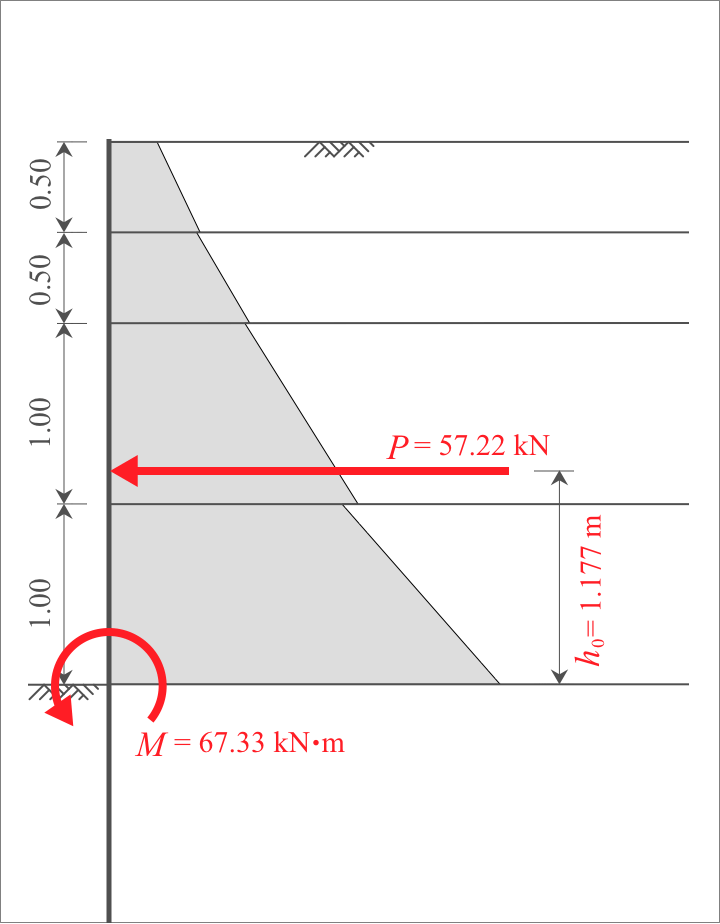
• 側圧の合力　$P= 57.22 \ \mathrm{kN}$
• 土留め壁に発生する最大曲げモーメント　$M= 67.33 \ \mathrm{kN \cdot m}$

合力の作用位置$h_0$は次の式で求めます。

$$ \begin{equation} \begin{split} h_0 &=\frac{M}{P} \ =\frac{67.33}{57.22}=1.177\ \mathrm{m} \end{split} \nonumber \end{equation} $$

1-3 土留め材の設定

(1)鋼材

設計条件として、鋼材の型式を「仮に」設定します。今回は、「H-200」にします。

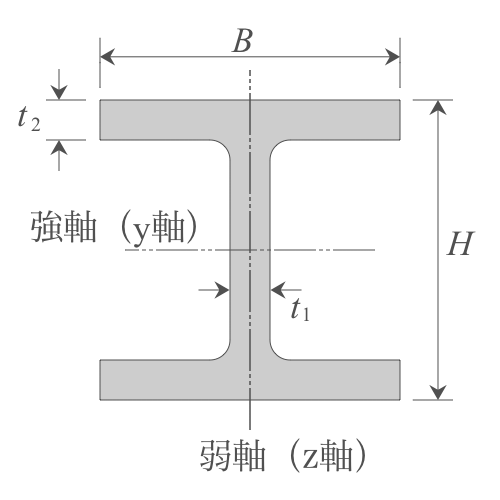
• 親杭断面寸法：H-200
• 高さ $H=200\ \mathrm{mm}$（H11道仮p.315より）
• 幅 $B=200\ \mathrm{mm}$
• ウェブ幅 $t_1=8\ \mathrm{mm}$
• フランジ厚 $t_2=12\ \mathrm{mm}$
• 断面二次モーメント $I= 4,720\ \mathrm{cm^4/m}$
• 断面係数 $Z=472\ \mathrm{cm^3}$
• 有効断面積 $A_s= 63.5\ \mathrm{cm^2}$

• 使用鋼材 SS400
• 軸方向引張許容応力度 $\sigma_{sa}= 210\ \mathrm{N/mm^2}$（H11道仮p.47より）
• せん断許容応力度 $\tau_{sa}= 120\ \mathrm{N/mm^2}$
• 支圧許容応力度 $ 315\ \mathrm{N/mm^2}$
• ヤング係数 $E = 200,000\ \mathrm{N/mm^2}$（H11道仮p.46より）
• 断面二次モーメントの有効率（根入れ長の計算）： $100$%（H11道仮p.153）
• 断面二次モーメントの有効率（断面力、変位の計算）： $100$%（H11道仮p.107）
• 断面係数の有効率（応力度の計算）： $100$%（H11道仮p.109）

後述する「根入れ長の計算」、「断面の計算」、「変位の計算」のいずれかで「NG」となった場合は、この設定を見直すことになります。（フローチャート参照）

H11道路土工仮設構造物工指針p.315には、H型鋼の断面性能が記載されています。設計に必要なところだけ抜粋して表にすると次のとおりです。

	高さ $H$ (mm)	幅 $B$ (mm)	ウェブ幅 $t_1$ (mm)	フランジ厚 $t_2$ (mm)	断面積 $A$ (cm²)	断面二次半径 $r_y$ (cm)	断面二次半径 $r_z$ (cm)	断面係数 $Z$ (cm³)
H-200	200	200	8	12	63.53	8.62	5.02	472
H-250	250	250	9	14	91.43	10.8	6.32	860
H-300	300	300	10	15	118.4	13.1	7.55	1,350
H-350	350	350	12	19	171.9	15.3	8.89	2,280
H-400	400	400	13	21	218.7	17.5	10.1	3,330

📌NOTE
H型鋼にはこのほかに、腹起し材と切ばり材に用いられる「リース加工品」と呼ばれる構造材があります。リース材の断面性能はH11道仮p.320に記載されています。 リース加工品には「孔」があけられており、断面係数などの数値が異なっています。 間違えないように注意しましょう。

(2)横矢板

• 使用材 米松
• 許容曲げ応力度 $\sigma_{wa}= 13.5\ \mathrm{N/mm^2}$（H11道仮p.54より）
• 許容せん断応力度 $\tau_{wa}= 1.05\ \mathrm{N/mm^2}$

2 根入れ長の計算(親杭の長さの決定)

自立式土留めの根入れ長は、「最小根入れ長」、「掘削底面の安定から決定される根入れ長」、「式（2－13－3）により求められる根入れ長」のうちの最大のものとします。（H11道仮p.153）

2-1 最小根入れ長

親杭なので、最小の根入れ長は「1.5m」とします。（H11道仮p.87）

$$ ℓ_{min}=1.5\ \mathrm{m} \nonumber $$

2-2 掘削底面の安定から決定される根入れ長

親杭横矢板土留めの工法は、止水性がないため、地下水位が低いときまたはポンプによる排水で十分である時に採用されます。

従って、砂地盤であってもボイリングの検討は省略できると考えられます。

2-3 式（2－13－3）により求められる根入れ長

(1)根入れ長の計算

H11道仮p.153に記載の式（2－13－3）より下記の式で根入れ長を求めます。

$$ ℓ_0=\frac{2.5}{\beta} \nonumber $$

ここに、

• $ℓ_0$：根入れ長（m）
• $\beta$：杭の特性値（m^－1）
  • $\displaystyle \beta=\sqrt[4]{\frac{k_{H1} \cdot B}{4 \cdot E \cdot I}}$
    • $k_{H1}$：水平方向地盤反力係数（kN/m³）　$k_{H1}=49,409\ \mathrm{kN/m^3}$　（計算方法は後述）
    • $B$：土留め壁の幅（m） 杭幅$B =0.20\ \mathrm{m}$
    • $E$：ヤング係数（kN/m²）　$E =200,000,000\ \mathrm{kN/m^2}$
    • $I$：土留め壁の断面二次モーメント（m⁴）$I =0.00004720\ \mathrm{m^4}$

$$ \beta=\sqrt[4]{\frac{49,409 \cdot 0.200}{4 \cdot 200,000,000 \cdot 0.00004720}}=0.720\ \mathrm{m^{-1}} \nonumber $$

📌NOTE
この$\beta$の算出には、水平方向地盤反力係数$k_{H1}$が必要です。ところが後述するとおり、$k_{H1}$の計算に$\beta$が必要となっています。 このため、「仮定値$\beta$」で$k_{H1}$を算出し、それを使って「計算値$\beta$」を求め、「仮定値－計算値」が「0」に収れんするまで仮定値を変化させる「繰り返し計算（Excelならばゴールシーク）」を行います。

よって、

$$ \begin{equation} \begin{split} ℓ_0 &= \frac{2.5}{0.720}\ =3.47\mathrm{m} \end{split} \nonumber \end{equation} $$

(2)水平方向地盤反力係数k_H1の計算

水平方向地盤反力係数$k_{H1}$は、まず、掘削底面から下に向かって距離「$1/\beta$の範囲」の各地層でそれぞれ計算します。そして、それらの平均値$\bar{k_{H1}}$を求めます。（H11道仮p.153,105）

各層の水平方向地盤反力係数は、下記の式で求めます。

$$ k_{H1}=\eta \cdot k_{H0} \left ( \frac{B_H}{0.3} \right )^{-3/4} \nonumber $$

ここに、

• $\eta$：壁体形式に関わる係数
  • $\eta = B_0 / B_f = 1.5 / 0.20 = 7.5$
  • ただし、$\eta \leqq 4$という条件があるため、
  • $\eta = 4 $
    • $B_0$：親杭中心間隔（m）$B_0=1.5$
    • $B_0$：親杭フランジ幅（m）$B_f=0.20$
• $k_{H0}$：直径30㎝の剛体円板による平板載荷試験の値に相当する水平方向地盤反力係数（kN/m³）
  • $\displaystyle k_{H0}=\frac{1}{0.3}\cdot \alpha \cdot E_0$
    • $\alpha$：地盤反力係数の推定に用いる係数（標準貫入試験による場合、$\alpha =1$）
    • $E_0$：測定または推定した設計の対象とする位置での地盤の変形係数（kN/m²）
      • $E_0=2,800 \cdot N$
• $B_H$：換算載荷幅（m）（連続壁の場合、$B_H=10\ \mathrm{m}$）

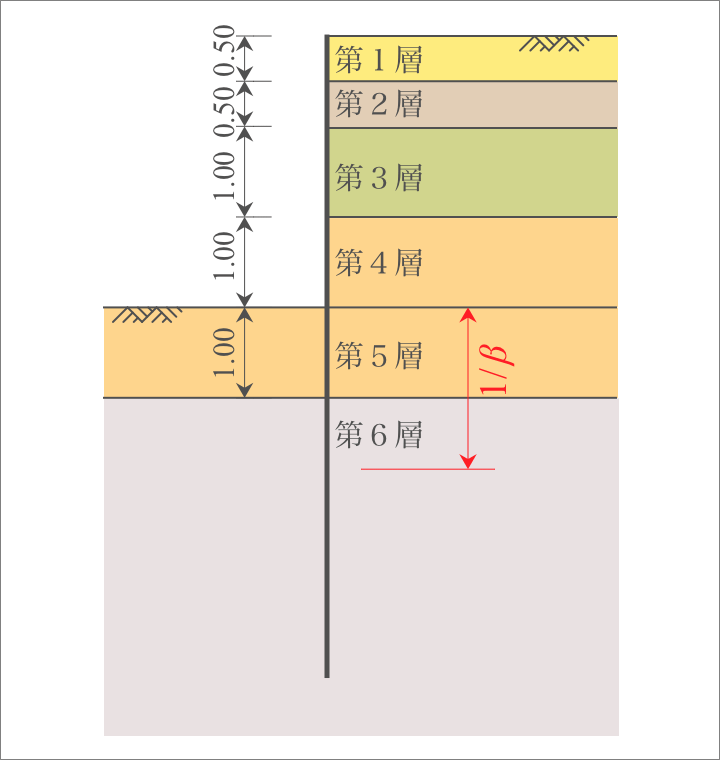
よって、掘削底面より下方向の距離「 $1/\beta$の範囲」で、各層の値は表計算すると下記のとおり。

	層厚	N値	$\alpha \cdot E_0$	$k_{H0}$	$k_{H1}$	$k_{H1} \cdot h$ (kN/m²)
5層	1.00	15	42,000	140,000	40,367	40,367
6層	0.39	27	75,600	252,000	72,661	28,257
$1/\beta=$	1.39				$\sum$	68,624

よって、水平方向地盤反力係数の平均値$\bar{k_{H1}}$は

$$ \begin{equation} \begin{split} \bar{k_{H1}} &= \frac{\sum(k_{H1} \cdot h)}{1/\beta}\\[5px] &= \frac{68,624}{1.39}\\[5px] &=49,409\ \mathrm{kN/m^3} \end{split}\nonumber \end{equation} $$

となります。

📌NOTE
上記のとおり、水平方向地盤反力係数$k_{H1}$の算出には、$1/\beta$を決定する必要があります。 しかし、先に説明したとおり、$1/\beta$の算出に$k_{H1}$が必要であることから、繰り返し計算法（Excelならばゴールシーク）で$\beta$を計算することになります。 このため、電卓と紙で計算し、答えを導くことが事実上困難です。これが仮設工を難解にしている原因だと思います。

2-4 根入れ長の比較と決定

自立式土留めの根入れ長は、それぞれの計算により求められる根入れ長のうち最大のものとする。

計算方法	計算結果
最小根入れ長	$ℓ_{min}=1.50$
掘削底面の安定から決定される根入れ長	省略
式（2－12－3）により求められる根入れ長	$ℓ_0=3.47$

よって、根入れ長$D=3.47\ \mathrm{m}$

📌NOTE
「道路土工仮設構造物工指針」において、「自立式土留め」の場合は、上記のとおり３つの根入れ長を計算します。 一方、「トンネル標準示方書（開削工法編）・同解説」では、「つりあい根入れ長」を計算するよう記載されています。 条件にもよりますが、ついあい根入れ長は、他の計算方法による根入れ長より大きくなるようです。

2-5 親杭の長さ

親杭の長さは、「掘削深さ」に「根入れ長」を加え、0.5m単位で切り上げる。

$$ \begin{equation} \begin{split} L &= H+D\\[5px] &= 3.00+3.47\\[5px] &= 6.47\\[5px] &\fallingdotseq 6.5\ \mathrm{m} \end{split} \nonumber \end{equation} $$

ただし、リース材の標準保有長さ（H11道仮p.321）の範囲外、最小長さ未満の場合は、型式を見直すこと。（保有長さは地域により異なる。）

H-200については、

• 標準保有長さ　4.0～8.0m
• 最小長さ　4.0m

であるため、L=6.5mはOK。

3 断面の計算

3-1 最大曲げモーメント

土留め壁の断面計算に用いる曲げモーメントは、下式により計算します。（H11道仮p.154）

$$ \begin{equation} M_{max} =\frac{P}{2\cdot\beta} \sqrt{(1+2\cdot \beta\cdot h_0)^2 +1}\ \cdot \exp \left( -\tan^{-1}\frac{1}{1+2\cdot \beta \cdot h_0} \right) \nonumber \end{equation} $$

ここに、

• $M_{max}$：断面計算用の土留め壁に発生する最大曲げモーメント（kN・m）
• $P$：側圧の合力（kN）$P =57.22\ \mathrm{kN}$
• $h_0$：掘削平面から合力の作用位置までの高さ（m）　$h_0 =1.177\ \mathrm{m}$
• $\beta$：杭の特性値（m^－1）$\beta=0.720$

よって、

$$ \begin{equation} \begin{split} M_{max} &=\frac{57.22}{2\,\cdot 0.720} \sqrt{(1+2\,\cdot 0.720\, \cdot 1.177)^2 +1}\; \exp \left( -\tan^{-1}\frac{1}{1+2\,\cdot 0.720\, \cdot 1.177} \right)\\[5px] &= 80.0\,\mathrm{kN \cdot m} \end{split} \nonumber \end{equation} $$

3-2 曲げ応力度の照査

親杭に発生する最大曲げ応力度$\sigma_{max}$が、「1-3. 土留め材の設定」で決めた許容応力度$\sigma_{sa}$以下であれば「OK」と判定し、「4. 変位の計算」に進みます。

許容応力度を超えた場合は「NG」と判定し、「1-3. 土留め材の設定」に戻り、親杭断面寸法を変えることになります。

土留め材に発生する最大曲げ応力度は、次の式で計算します。

$$ \sigma_{max}=\frac{M_{max}}{Z \cdot e} \nonumber $$

ここに

• $\sigma_{max}$：親杭に発生する最大曲げ応力度（N/mm²）
• $Z$：断面係数（m³/m）　$Z=472.0 \ \mathrm{cm^3/m}$　$=0.0004720 \ \mathrm{m^3/m}$
• $e$：断面係数の有効率（応力度の計算）$e=100$%

よって、

$$ \begin{equation} \begin{split} \sigma &=\frac{80.0}{0.0004720 \cdot 1.0}\\[5px] &= 169,492\,\mathrm{kN/m^2}\\[5px] &= 169.5\ \mathrm{N/mm^2} \ \leqq \sigma_{sa}=210.0\ \mathrm{N/mm^2}\ \mathrm{OK} \end{split}\nonumber \end{equation} $$

4 変位の計算

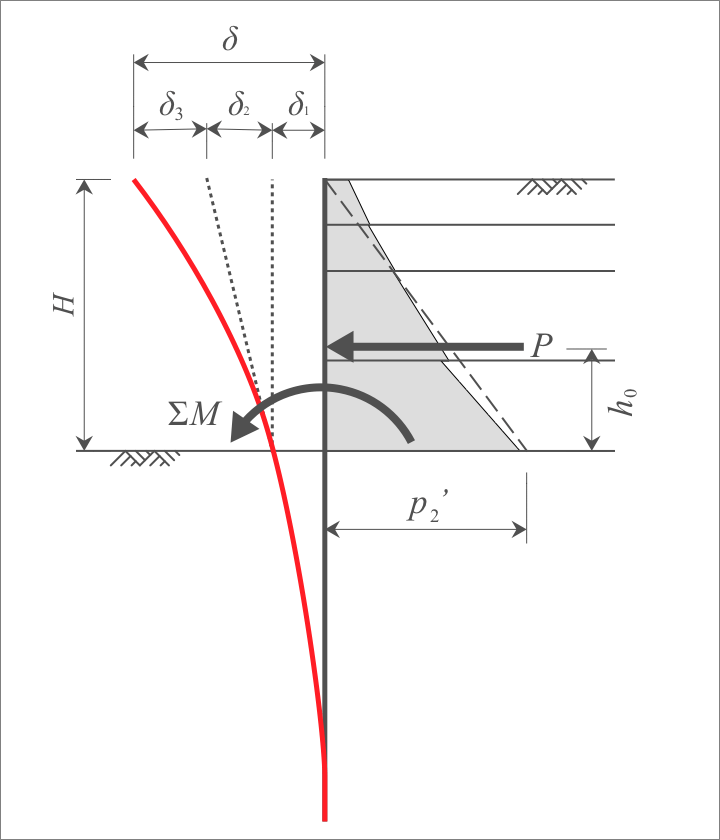
自立式土留め壁頭部の変位量は３つの変位量を足し合わせて求めます。

4-1 掘削底面での変位量

掘削底面での変位量は、下式で求めます。（H11道仮p154）

$$ \delta_1 = \frac{(1+\beta \cdot h_0)}{2 \cdot E \cdot I \cdot \beta \ ^3}P \nonumber $$

ここに、

• $\beta$：杭の特性値（m^ー1）　$\beta=0.720$
• $h_0$：掘削平面から合力の作用位置までの高さ（m）　$h_0=1.177 \ \mathrm{m}$
• $E$：ヤング係数（kN/m2）　$E=200,000,000 \ \mathrm{kN/m^2}$
• $I$：土留め壁の断面二次モーメント（m⁴）　$I=0.00004720 \ \mathrm{m^4}$
• 断面二次モーメントの有効率（断面力、変位の計算）$100$%
• $P$：側圧の合力（kN）　$P=57.22 \ \mathrm{kN}$

よって、

$$ \begin{equation} \begin{split} \delta_1 &=\frac{(1+0.720 \cdot 1.177)}{2 \cdot 200,000,000 \cdot 0.00004720 \cdot 1.00 \cdot 0.720 \ ^3} \cdot 57.22\\[5px] &= 0.0150\ \mathrm{m} \end{split}\nonumber \end{equation} $$

4-2 掘削底面でのたわみ角による変位量

掘削底面でのたわみ角による変位量は、下式で求めます。（H11道仮p155）

$$ \delta_2 = \frac{(1+2 \cdot \beta \cdot h_0)}{2 \cdot E \cdot I \cdot \beta \ ^2}P \cdot H \nonumber $$

ここに、

• $H$：掘削深さ（m）　$H=3.00$

よって、

$$ \begin{equation} \begin{split} \delta_2 &=\frac{(1+2 \cdot 0.720 \cdot 1.177)}{2 \cdot 200,000,000 \cdot 0.00004720 \cdot 1.00 \cdot 0.720 \ ^2} \cdot 57.22 \cdot 3.00\\[5px] &= 0.0473\ \mathrm{m} \end{split}\nonumber \end{equation} $$

4-3 掘削底面以上の片持ちばりのたわみ

掘削底面以上のたわみは、下式で求めます。（H11道仮p155）

$$ \delta_3 = \frac{p_2\ ^\prime \cdot H^4}{30 \cdot E \cdot I} \nonumber $$

ここに、

• $p_2 \ ^\prime$：モーメントを等価とする三角形分布荷重の掘削底面での荷重強度（kN/m）
  • $\displaystyle p_2 \ ^\prime = \frac{6 \cdot \sum M}{H^2}$
    • $\sum M$：土留め壁に発生する最大曲げモーメント（kN・m）　$\sum M = 67.33$
  • よって、
  • $\displaystyle p_2 \ ^\prime = \frac{6 \cdot 67.33}{3.00^2} \ =44.88\ \mathrm{kN/m}$

よって、

$$ \begin{equation} \begin{split} \delta_3 &= \frac{44.88 \cdot 3.00^4}{30 \cdot 200,000,000 \cdot 0.00004720 \cdot 1.00}\\[5px] &= 0.0128\ \mathrm{m} \end{split} \nonumber \end{equation} $$

4-4 変位量の照査

上記の変位量３つの合計が、「1-1. 設計条件の設定」で決めた許容変位量$\delta_a$以下であれば「OK」と判定し、終了します。

許容変位量を超えた場合は「NG」と判定し、「1-3. 土留め材の設定」に戻って親杭断面寸法を変えます。

$$ \begin{equation} \begin{split} \delta &= \delta_1 +\delta_2 +\delta_3\\[5px] &= 0.0150 + 0.0473 + 0.0128\\[5px] &= 0.075\,\mathrm{m} \ \leqq \ \delta_a = 0.090\,\mathrm{m}\ \mathrm{OK} \end{split} \nonumber \end{equation} $$

5 横矢板の設計

横矢板は等分布荷重が作用する単純ばりとして計算を行う。（H11道仮p.110）

5-1 土圧強度とスパン

土圧強度は「1-2. 設計条件に基づく外力の計算」より最深部での土圧とする。

土圧強度：$w=20.98\ \mathrm{kN/m^2}$

単純ばりのスパン$ℓ_2$は、親杭間隔$a$から、両端それぞれの親杭の幅の半分$B/2$を差し引く長さとする。

$$ \begin{equation} \begin{split} ℓ_2 &= a - B / 2 \times 2 \\[5px] &= 1.50 - 0.20 / 2 \times 2 \\[5px] &= 1.30\ \mathrm{m} \end{split}\nonumber \end{equation} $$

土留め板の深さ方向の単位幅$b_w$は下記のとおりとする。

$b_w=1,000\ \mathrm{mm}\ = 1\ \mathrm{m}$

5-2 必要板厚の計算

土留め板に作用する最大の作用モーメント$M_w$を求めてから、必要板厚$t$を算出する。（H11道仮p.111）

等分布荷重が作用する単純ばりであるため、公式より作用モーメント$M_w$は次のとおり。

$$ \begin{equation} \begin{split} M_w &= \frac{1}{8} \cdot w \cdot ℓ_2^2 \\[5px] &= \frac{1}{8} \cdot 20.98 \cdot 1.30^2 \\[5px] &= 4.43\ \mathrm{kN・m} \end{split}\nonumber \end{equation} $$

必要板厚$t$は、次式で求める。ただし、最小板厚は、30mmとする。

$$ \begin{equation} \begin{split} t &=\sqrt{\frac{6 \cdot M_w}{b_w \cdot \sigma_{wa}}} \\[5px] &=\sqrt{\frac{6 \cdot 4.43}{1 \cdot 13,500}} \\[5px] &= 0.0444\ \mathrm{m} \\[5px] &= 44.4\ \mathrm{mm} \end{split}\nonumber \end{equation} $$

5-3 せん断応力度の照査

土留め板に作用する作用せん断力$Q_w$は、単純張りに作用する分布荷重の公式により算出する。（H11道仮p.111）

$$ \begin{equation} \begin{split} Q_w &= \frac{1}{2} \cdot w \cdot ℓ_2 \\[5px] &= \frac{1}{2} \cdot 20.98 \cdot 1.30 \\[5px] &= 13.64\ \mathrm{kN} \end{split}\nonumber \end{equation} $$

「1-3. 土留め材の設定」で決めた許容せん断応力$\tau_{wa}$以下であれば「OK」と判定し、終了します。

許容せん断応力度を超えた場合は「NG」と判定し、「1-3. 土留め材の設定」に戻って使用材を変えます。

$$ \begin{equation} \begin{split} \tau &= \frac{Q_w}{b \cdot t}\\[5px] &= \frac{13.64}{1 \cdot 0.0444}\\[5px] &= 307.3\,\mathrm{kN/m^2} \ \leqq \ \tau_{wa} = 1,050\,\mathrm{kN/m^2}\ \mathrm{OK} \end{split} \nonumber \end{equation} $$

これで設計終了です。

結果は、「H-200の親杭で、長さ6.5m（根入れ長3.47m）」、「米松の横矢板で、必要板厚44.4mm」となりました。

📌NOTE
横矢板の設計では、「許容曲げ応力度」から必要板厚を算出し、せん断応力度を照査します。 この設計方法は、曲げ応力度が板厚を決定する支配的な要素であるためと考えられます。

エクセルブック

計算を記載したエクセルブックは下記からダウンロードしてください。

DOWNLOAD

シートに保護をかけていますが、パスワードは設定していません。

分かりにくかったり、間違いを見つけられた場合は、ご連絡いただけると幸いです。