変形係数
変形係数とは?
変形係数とは、土または地盤における「応力ひずみ線図の勾配」です。
変形係数が、大きい(勾配が急)と変形しづらい(固い)ことになります。
鉄筋の「応力ひずみ線図の勾配」を「ヤング係数」と呼ぶのに対し、土または地盤の場合の「応力ひずみ線図の勾配」を「変形係数」と呼びます。
土または地盤は、弾性体であるバネのように応力とひずみの関係が一定ではなく、応力ひずみ線図は、曲線となります。
しかし、土木や建築の構造物設計においては、地盤をバネと仮定して設計した方が、簡略で分かりやすくできます。
このため、変形係数は、応力ひずみ線図の「特定の応力」における「ひずみ量」を読み取り、勾配を求めることになります。
求め方
変形係数$E$を測定・推定するための試験と計算方法は、次のとおりです。
供試体の一軸圧縮試験(三軸圧縮試験)
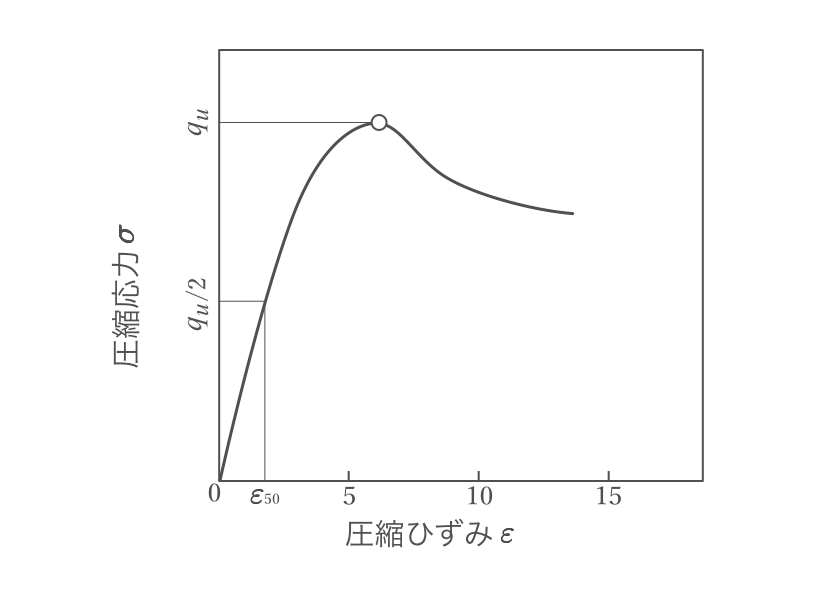
一軸圧縮試験では、圧縮強度の半分に相当する応力における応力ひずみ線図上の点と原点とを結ぶ直線の勾配(割線変形係数)を変形係数$E_{50}$と規定しています。
ここに、
- $E_{50}$:変形係数(MN/m²)
- $q_u$:一軸圧縮強度(kN/m²)
- 三軸圧縮試験の場合、$\sigma_1 - \sigma_3$:主応力差
- $\varepsilon_{50}$:圧縮強度が$q_u/2$のときの軸ひずみ(%)
- 出所:JIS規格A1216
単位をkN/m²に変換すると、
平板載荷試験
平板載荷試験の場合、変形係数$E_s$は、載荷圧力~変位曲線のうち新規載荷荷重部を包絡する直線の勾配から次式で算出する。
ここに、
- $E_s$:変形係数(kN/m²)
- $I_s$:基礎底面の形状と剛性によって決まる係数(剛な円形の場合0.79)
- $\nu$:ポアソン比(砂質土0.3、粘性土0.5)
- $B$:載荷板の直径(m)
- $\varDelta p$:載荷圧力の変化量で、設計荷重を考慮して設定する(kN/m²)
- $\varDelta S$:$\varDelta p$に対応する沈下量で、載荷圧力~沈下量曲線から求める(m)
- 出所:地盤工学会「地盤調査―基本と手引き―」
孔内水平載荷試験
変形係数$E_p$は、圧力~変位量(または体積変化量)曲線における直線部分の勾配から次式で算出する(A型の場合)。
ここに、
- $E_p$:変形係数(kN/m²)
- $\nu$:ポアソン比
- $\varDelta p$:圧力~変位量曲線の直線部における圧力増分(kN/m²)
- $\varDelta r$:$\varDelta p$に対応する変位増分(m)
- $r_m$:$\displaystyle \frac{\varDelta p}{\varDelta r}$算定区間の中間半径(m)
- 出所:地盤工学会「地盤調査―基本と手引き―」
標準貫入試験
標準貫入試験より得られる「N値」と、孔内水平載荷試験で得られる変形係数との関係は、次式のとおり近似できます。
ここに、
- なお、単位はkg/cm²である。
- 出所:吉中竜之進:地盤反力係数とその載荷幅による補正、土木研究所資料、第299号、1967 p.14
単位をkN/m²に変換すると、
各試験より得られる変形係数間の関係
既往の研究によって、
という関係が得られています。
ここに、
- $E_s$:平板載荷試験による変形係数(kN/m²)
- $E_p$:孔内水平載荷試験による変形係数(kN/m²)
- $E_{50}$:一軸圧縮試験(三軸圧縮試験)による変形係数(kN/m²)
実際に、道路橋示方書(H29) p.422では、地盤反力係数を算出するための係数$\alpha$「常時、暴風時」において、
- 平板載荷試験「1」
- 孔内水平載荷試験「4」
- 一軸圧縮試験、三軸圧縮試験はともに「4」
となっています。
また、標準貫入試験のN値より算出する場合、
$E_s=2800N$
とされています。
これは、平板載荷試験の変形係数は、孔内水平載荷試験のそれの4倍であり、$E_p=700N$であることから、
となります。
使い方
変形係数は「直接基礎」や「杭基礎」の設計における「鉛直方向地盤反力係数」、「水平方向地盤反力係数」の算出に用いられます。
具体例は次のとおり。